GUIpowermean
GUIpowermean shows the necessary calculations to obtain the power (generalized) mean in a GUI.
Description
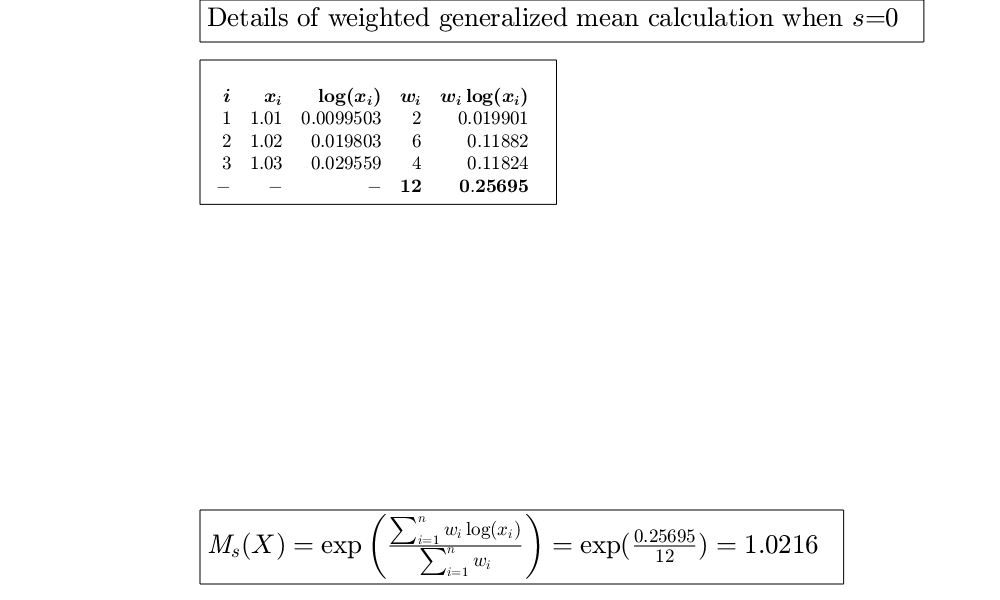
The power mean (also known as generalized mean, or Holder mean or Kolmogorov-Negumo function of the mean), is an abstraction of the Pythagorean means. It includes the harmonic $(s=-1)$, geometric ($s\rightarrow 0$), and arithmetic ($s=1$), quadratic ($s=2$), cubic mean ($s=3$). When $s \rightarrow -\infty$ the power mean tends to $x_{min}$ and when $s\rightarrow +\infty$ the power mean tends to $x_{max}$. http://en.wikipedia.org/wiki/Generalized_mean
Examples
Input Arguments
Output Arguments
References
Milioli, M.A., Riani, M., Zani, S. (2019), "Introduzione all'analisi dei dati statistici (Quarta edizione ampliata)". [MRZ]
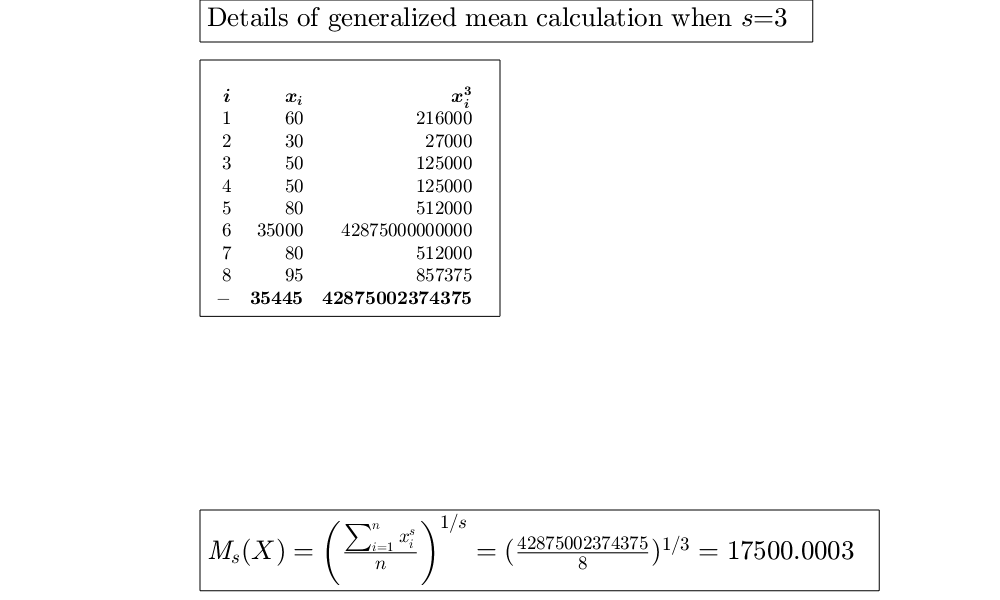
 Example of use of the cubic mean.
Example of use of the cubic mean.