LTStsLSmult

LTStsLSmult extends LTSts to the detection of multiple Level Shifts in time series

expand all in page

Syntax

Description

example

out =LTStsLSmult(y) A synthetic example with all default arguments.

example

out =LTStsLSmult(y, Name, Value) A synthetic example with optional arguments msg and plots.

Examples

expand all

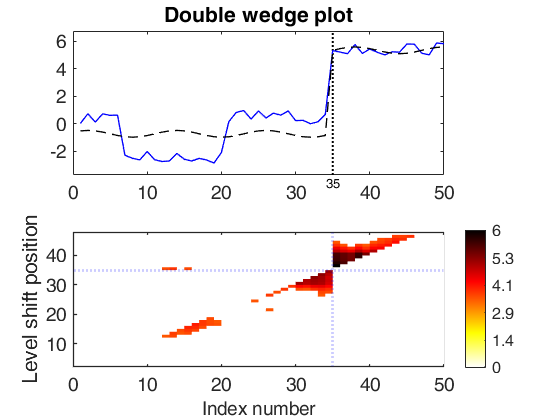
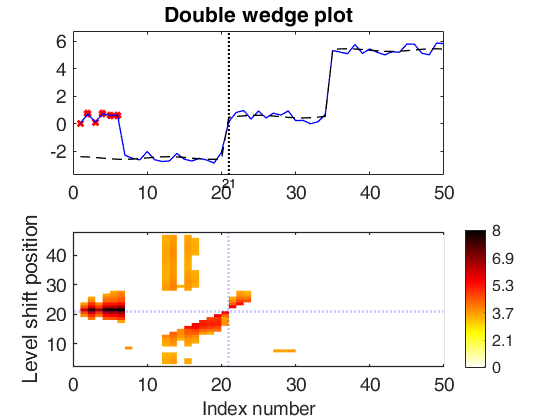
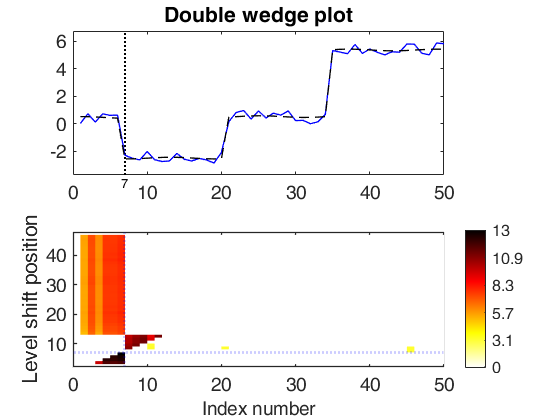
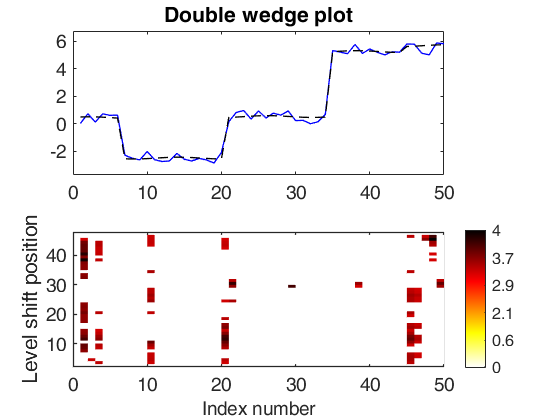
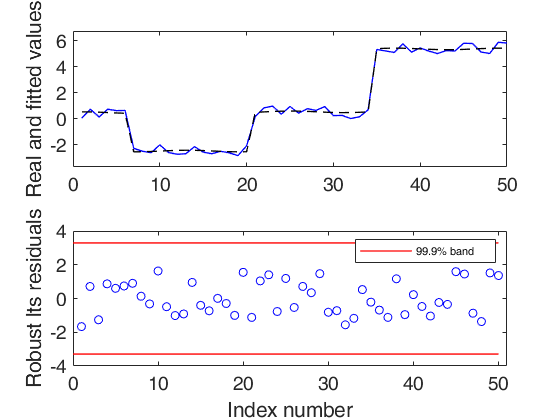
  • A synthetic example with all default arguments.

    • Y=rand(50,1);
Y(35:end)=Y(35:end)+5;
Y(7:20)=Y(7:20)-3;
out  = LTStsLSmult(Y,'msg',true,'plots',1);

  • A synthetic example with optional arguments msg and plots.

    • Y=rand(50,1);
Y(35:end)=Y(35:end)+5;
Y(7:20)=Y(7:20)-3;
out  = LTStsLSmult(Y,'msg',true,'plots',1);
    significant LS at position 35 (pval = 7.1054e-15)
significant LS at position 21 (pval = 0)
significant LS at position 7 (pval = 0)
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • Trade data examples.

    • Two examples taken from the (extended version of the) series in: Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". 

    load TTplant  % KE-GB
load TTsugar   % UA-LT
yin1   = plant{:,1};
yin2   = sugar{:,1};
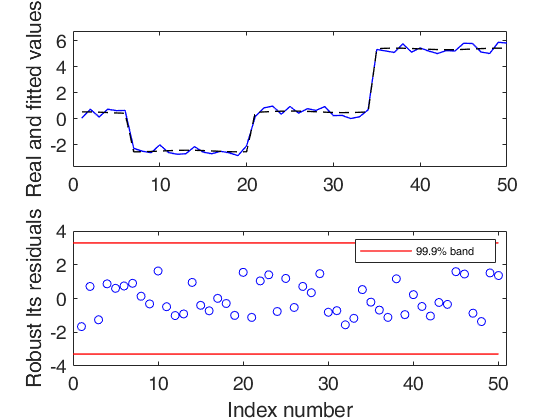
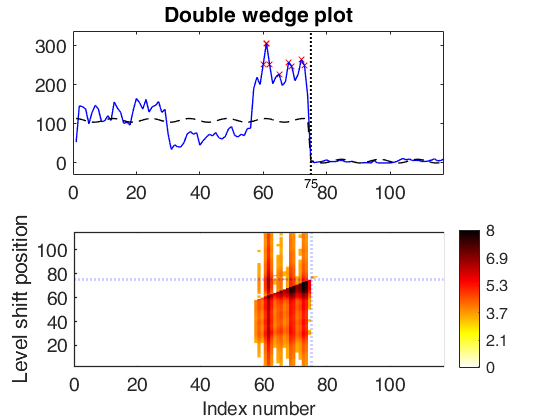
out1  = LTStsLSmult(yin1,'msg',true,'plots',1);
sgtitle('P12119085_KE_GB','interpreter','none','Fontsize',20);
pause(1);
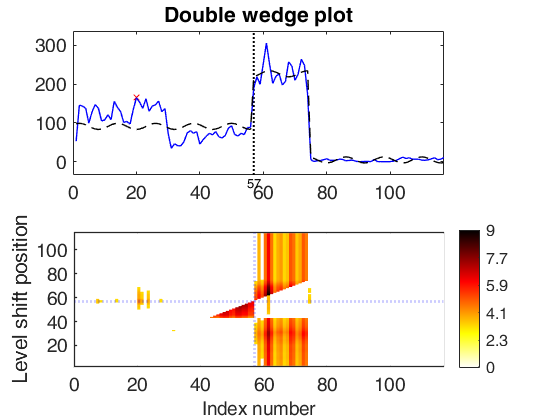
out2  = LTStsLSmult(yin2,'msg',true,'plots',1);
sgtitle('P17049075_UA_LT','interpreter','none','Fontsize',20);
    significant LS at position 75 (pval = 0)
significant LS at position 57 (pval = 0)
significant LS at position 30 (pval = 0)
significant LS at position 60 (pval = 0)
significant LS at position 36 (pval = 1.7337e-10)
significant LS at position 79 (pval = 4.793e-06)
significant LS at position 41 (pval = 0)
significant LS at position 101 (pval = 0.0096827)
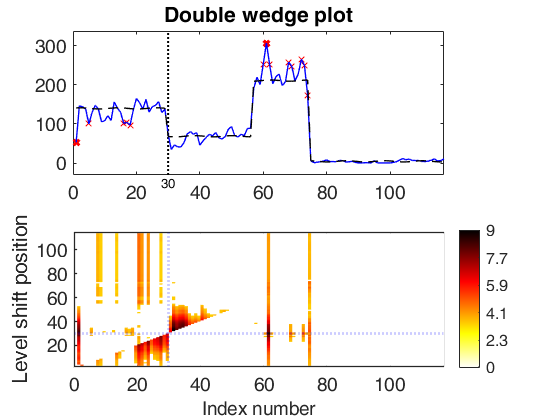
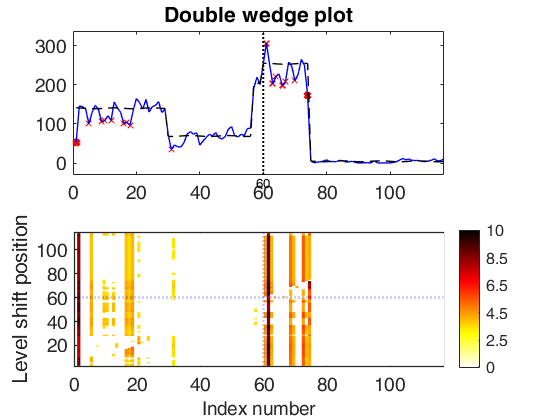
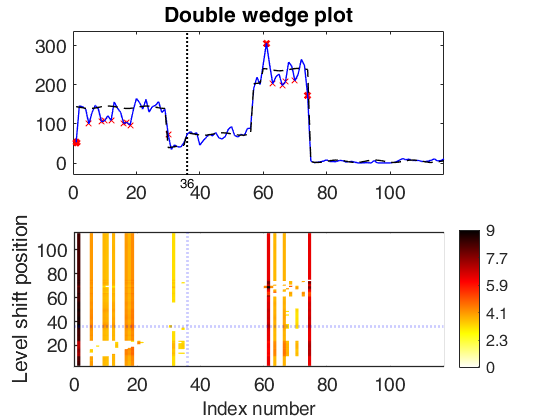
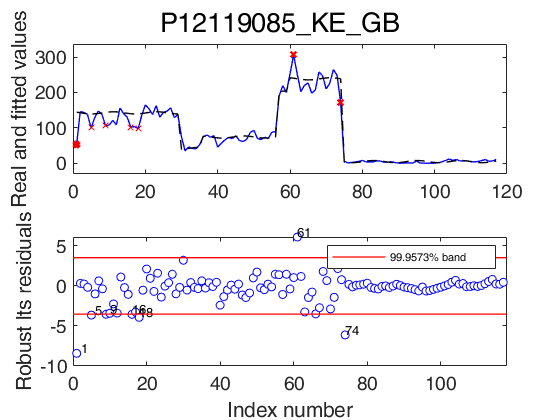
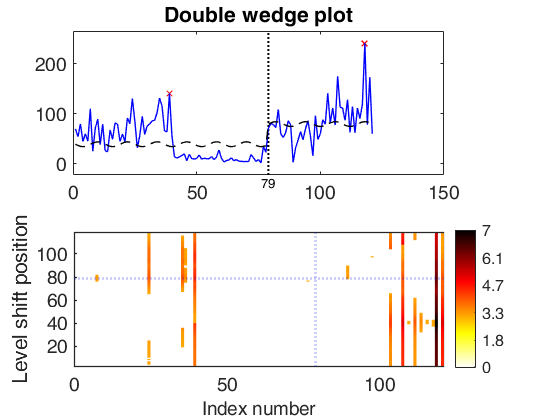
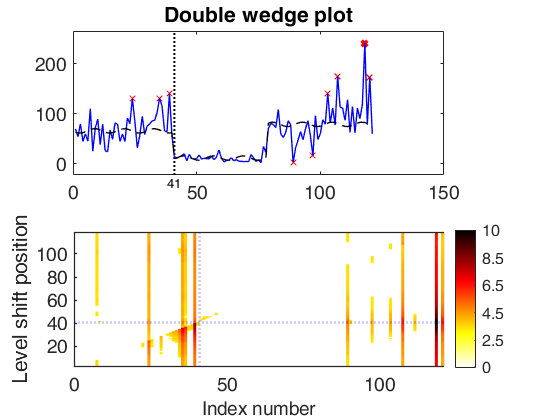
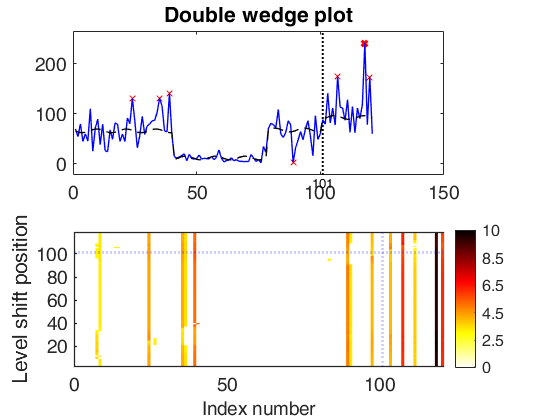
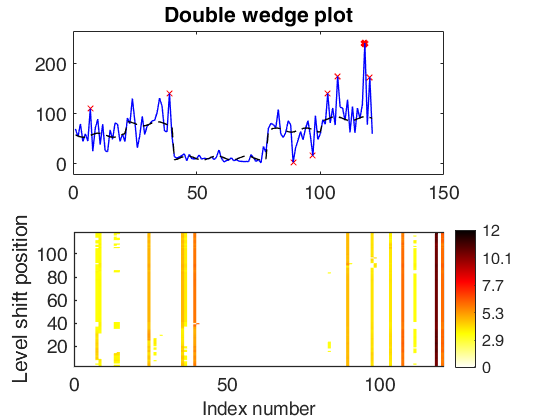
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Multiple level shift and variable selection.

    • Example 1. Detection of multiple Level Shifts followed by variable selection on the dataset of example before. 

    load TTsugar   % UA-LT
yin2   = sugar{:,1};
out = LTStsLSmult(yin2,'maxLS',4,'alphaLTS',0.01,...
'alphaLS',0.01,'thresLS',0.01,'plots',1,'msg',1);
outX = out.outX;
model.trend = 2;
model.lshift = 0;
model.seasonal=303;
model.X = outX(:,3:end);
[out_model_1, out_reduced_1] = LTStsVarSel(yin2,'model',model,'plots',1);
[out_LTSts]=LTSts(yin2,'model',out_model_1,...
'plots',1,'msg',0,'dispresults',1,'SmallSampleCor',1,'conflev',1-0.01/length(yin2));

  • Multiple level shift and variable selection.

    • Example 2. Detection of multiple Level Shifts followed by variable selection on the dataset of example before. 

    load TTplant 
yin2   = plant{:,1};
out = LTStsLSmult(yin2,'maxLS',4,'alphaLTS',0.01,...
'alphaLS',0.01,'thresLS',0.01,'plots',1,'msg',1);
outX = out.outX;
model=struct;
model.trend = 2;
model.lshift = 0;
model.seasonal=303;
model.X = outX(:,3:end);
[out_model_1, out_reduced_1] = LTStsVarSel(yin2,'model',model,'plots',1);
[out_LTSts]=LTSts(yin2,'model',out_model_1,...
'plots',1,'msg',0,'dispresults',1,'SmallSampleCor',1,'conflev',1-0.01/length(yin2));

  • Multiple level shift and variable selection.

    • Example 3. Simulated data with the platonic idea of multiple LS. 

    rng('default')
%data generation
A = [ones(1,50) 25*ones(1,50) 50*ones(1,50) 75*ones(1,50)] + rand(1,200);
figure;
plot(A,'-')
%detection of multiple LS 
close all
out = LTStsLSmult(A',...
'maxLS',5,'alphaLTS',0.01,...
'alphaLS',0.01,'thresLS',0.01,'plots',1,'msg',1);
cascade
%plot LS
close all
figure;
plot(A,'-')
gc=gca;
ylimits = gc.YLim;
xlimits = gc.XLim;
hold on
for i=1:length(out.LSpos)
line([out.LSpos(i) out.LSpos(i)],[ylimits(1) ylimits(2)],'color','k','linewidth',1,'linestyle','--');
end
%variable selection, given the multiple LS 
close all
model.trend = 2;
model.lshift = 0;
model.seasonal = 303;
model.X = out.outX(:,3:end);
[out_model_1, out_reduced_1] = LTStsVarSel(A','model',model,'plots',1);
cascade

    Input Arguments

    expand all

    y — Time series to analyze. Vector.

    A row or a column vector with T elements, which contains the time series.

    Data Types: double.

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'alphaLS', 0.1 , 'alphaLTS',0.1 , 'bdp',0.4 , 'maxLS', 8 , 'model', model , 'msg',true , 'sampleLS', [5 16 27 35] , 'startLS', 15 , 'thresLS', 50 , 'plots',1

    alphaLS —maximum pvalue to consider a Level Shift significant.scalar.

    It is a threshold for detecting significant Level Shifts. Default is 0.01.

    Example: 'alphaLS', 0.1

    Data Types: double

    alphaLTS —complement of the confidence level.scalar.

    Scalar between 0 and 1 containing the complement (to 1) of the confidence level which is used to declare units as outliers in each call to LTSts. Usually alpha = 0.05/T, 0.025/T, 1-0.01/T (simultaneous alpha). Default value is 0.01/T where T=length(y).

    Example: 'alphaLTS',0.1

    Data Types: double

    bdp —breakdown point.scalar.

    It measures the fraction of outliers the algorithm should resist. In this case any value greater than 0 but smaller or equal than 0.5 will do fine. Default value 0.1.

    Example: 'bdp',0.4

    Data Types: double

    maxLS —maximum number of Level Shifts.scalar.

    Maximum number of Level Shifts that the function looks for. Default is 5.

    Example: 'maxLS', 8

    Data Types: double

    model —model type.structure.

    A structure which specifies the model which will be used. The model structure contains the following fields:

    Value Description
    s

    scalar (length of seasonal period). For monthly data s=12 (default), for quartely data s=4, ...
    trend

    scalar (order of the trend component).

    trend = 0 implies no trend;

    trend = 1 implies linear trend with intercept (default);

    trend = 2 implies quadratic trend;

    trend = 3 implies cubic trend.

    Admissible values for trend are, 0, 1, 2 and 3.
    seasonal

    scalar (integer specifying number of frequencies, i.e. harmonics, in the seasonal component. Possible values for seasonal are $0,1, 2, ..., [s/2]$, where $[s/2]=floor(s/2)$.

    If seasonal =0 we assume there is no seasonal component.

    If seasonal =1 (default) we have: $\beta_1 \cos( 2 \pi t/s) + \beta_2 sin ( 2 \pi t/s)$;

    if seasonal =2 we have: $\beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s) + \beta_3 \cos(4 \pi t/s) + \beta_4 \sin (4 \pi t/s)$.

    Note that when $s$ is even the sine term disappears for $j=s/2$ and so the maximum number of trigonometric parameters is $s-1$.

    If seasonal is a number greater than 100 then it is possible to specify how the seasonal component grows over time.

    For example, seasonal = 101 implies a seasonal component which just uses one frequency which grows linearly over time as follows: $(1+\beta_3 t)\times ( \beta_1 cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s))$.

    For example, seasonal =201 implies a seasonal component which just uses one frequency which grows in a quadratic way over time as follows: $(1+\beta_3 t + \beta_4 t^2)\times( \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s))$.

    seasonal =0 implies a non seasonal model.

    In the paper RPRH to denote the number of frequencies of the seasonal component symbol B is used, while symbol G is used to denote the order of the trend of the seasonal component.

    Therefore, for example, model.seasonal=201 corresponds to B=1 and G=2, while model.seasonal=3 corresponds to B=3 and G=0;
    X

    matrix of size T-by-nexpl containing the values of nexpl extra covariates which are likely to affect y.
    ARp

    vector with non negative integer numbers specifying the autoregressive components. For example: model.ARp=[1 2] means a AR(2) process;

    model.ARp=2 means just the lag 2 component;

    model.ARp=[1 2 5 8] means AR(2) + lag 5 + lag 8;

    model.ARp=0 (default) means no autoregressive component.
    ARtentout

    matrix of size r-by-2 containing the list of the units declared as outliers (first column) and corresponding fitted values (second column) or empty scalar. If model.ARtentout is not empty, when the autoregressive component is present, the y values which are used to compute the autoregressive component are replaced by model.tentout(:,2) for the units contained in model.tentout(:,1) Remark: the default model is for monthly data with no trend (1 parameter) + seasonal component with just one harmonic (2 parameters), no additional explanatory variables and no level shift that is model=struct;

    model.s=12;

    model.trend=0;

    model.seasonal=1;

    model.X=[];
    lshift

    0;

    Example: 'model', model

    Data Types: struct

    msg —Messages on the screen.boolean.

    Scalar which controls whether to display or not messages on the screen. If msg==true (default) messages are displayed on the screen about estimated time to compute the estimator and the warnings about 'MATLAB:rankDeficientMatrix', 'MATLAB:singularMatrix' and 'MATLAB:nearlySingularMatrix' are set to off else no message is displayed on the screen

    Example: 'msg',true

    Data Types: logical

    sampleLS —vector of the positions in which Level Shift should be tested.vector.

    It is be the vector for the parameter model.lshift of the LTSts function.

    Default is 3.

    Example: 'sampleLS', [5 16 27 35]

    Data Types: double

    startLS —first position in which Level Shift should be tested.scalar.

    It is the low extreme of the interval for the parameter model.lshift for the LTSts function.

    Default is 3.

    Example: 'startLS', 15

    Data Types: double

    thresLS —minimum length of the time series to look for Level Shift.scalar.

    In order to detect Level Shifts the series should have more than thresLS observations.

    Default is 20.

    Example: 'thresLS', 50

    Data Types: double

    plots —Plots on the screen.scalar.

    If plots = 1, a two panel plot will be shown on the screen.

    The upper panel contains the orginal time series with fitted values. The bottom panel will contain the plot of robust residuals against index number. The confidence level which is used to draw the horizontal lines associated with the bands for the residuals is specified in input option conflev.

    The default value of plot is 0 i.e. no plot is shown on the screen.

    Example: 'plots',1

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    A structure containing the following fields

    Value Description
    R2

    Scalar containing the goodness of fit.
    yhat

    Vector of the fitted values
    LSpos

    Vector of the positions of the detected Level Shifts
    LSpval

    Vector of the pvalues of the detected Level Shifts
    LSud

    Vector of the sign (positive or negative) of the detected Level Shifts residuals
    outliers

    Vector of the positions of the detected outliers
    outX

    Structure containing the final output of LTSts. It is useful later to run LTStsVarSel with in the parameter model also the item model.X, containing the dummy variables with Level Shifts positions.

    References

    Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". [RPRH]

    See Also

    | |

    This page has been automatically generated by our routine publishFS