SDest

SDest computes Stahel-Donoho robust estimator of dispersion-location

expand all in page

Syntax

Description

example

out =SDest(Y) SDest with all default options.

example

out =SDest(Y, Name, Value) SDest with optional arguments.

example

[out, varargout] =SDest(___) SDest with exctracted subsamples.

Examples

expand all

  • SDest with all default options.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[out]=SDest(Ycont);

  • SDest with optional arguments.

    • SDest with v+1 directions for each subsample (jpcorr=1). 

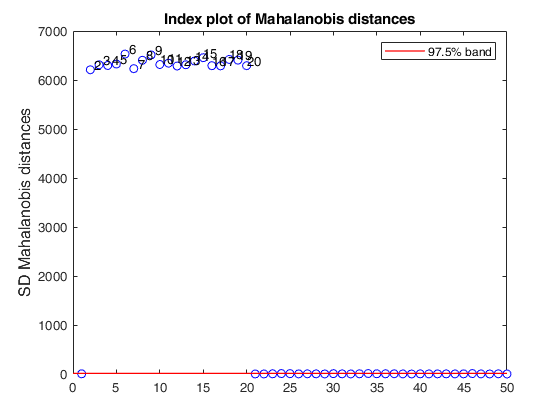
    % Produce plot of robust Mahalanobis distances
n=50;
v=5;
randn('state', 1256);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+4;
[out]=SDest(Ycont,'jpcorr',1,'plots',1);
    Warning: Using 'state' to set RANDN's internal state causes RAND, RANDI, and
RANDN to use legacy random number generators.  This syntax is not recommended.
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace the
old syntax. 
Total estimated time to complete Stahel-Donoho estimator:  0.20 seconds
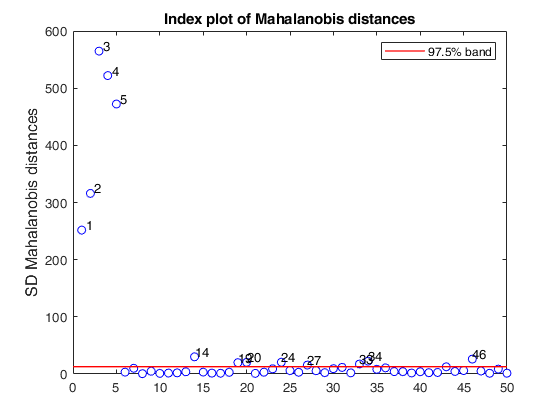
    Click here for the graphical output of this example (link to Ro.S.A. website).

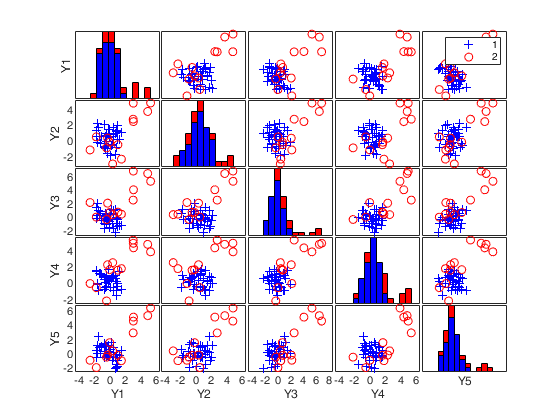
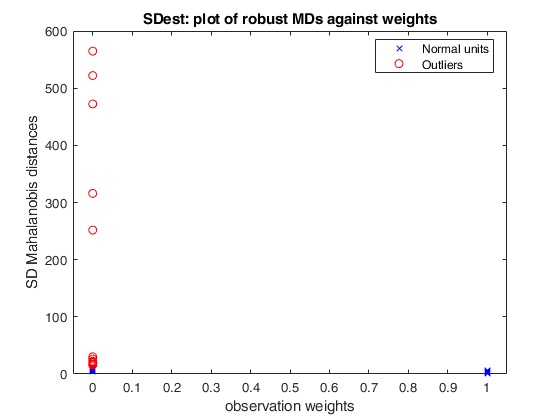
  • SDest with exctracted subsamples.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[out,C]=SDest(Ycont);

    Related Examples

    expand all

  • SDest jpcorr equal to 1.

    • v+1 directions for each subsample. Produce plot of robust Mahalanobis distances. 

    n=50;
v=5;
randn('state', 1256);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(2:20,3)=100;
[out]=SDest(Ycont,'jpcorr',1,'margin',3,'plots',1);
    Total estimated time to complete Stahel-Donoho estimator:  0.18 seconds 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision. 
Warning: Matrix is singular to working precision.
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • SDest with with Juan and Prieto adjustment.

    • jpcorr>1. Subsamples of size equal to v+5 are initially drawn (jpcorr=5). 

    % In each of them, the 4 units (=jpcorr-1) having the four
% largest MDs are then discarded from the subsample.
% For each subsample v+1 directions are computed.
% Produce plot of robust Mahalanobis distances.
n=50;
v=5;
randn('state', 1256);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(2:20,3)=5+1e-7*randn(19,1);
[out]=SDest(Ycont,'jpcorr',5,'plots',1,'nsamp',100000);
%  SDest with directions and robust standardized projection scores saved
[out]=SDest(Ycont,'jpcorr',0,'plots',1,'nsamp',1000,'dirsave',1,'rstprojsave',1);
% Compare the output of SD with the one produced by the fwd search
outFS=FSM(Ycont,'init',20);
% SDest with different choices for the weight functions.
n=100;
v=5;
randn('state', 1256);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
rndind = randsample(n,10);
Ycont(rndind,1)=20;
[outhub]=SDest(Ycont,'jpcorr',2, 'weight','huber', 'plots',1);
[outtuk]=SDest(Ycont,'jpcorr',2, 'weight','tukey', 'plots',1);
[outtuk025]=SDest(Ycont,'jpcorr',2, 'weight','tukey', 'nbp',0.25, 'plots',1);
[outzch]=SDest(Ycont,'jpcorr',2, 'weight','zch', 'plots',1);
[outzchK50]=SDest(Ycont,'jpcorr',2, 'weight','zch', 'K',50, 'plots',1);
% SDest with alternatives to the MAD.
n=50;
v=5;
randn('state', 1256);
Y=randn(n,v);
[outMAD]=SDest(Y,'jpcorr',5,'plots',1,'nsamp',10000);
[outSN]=SDest(Y,'jpcorr',5,'plots',1,'nsamp',10000, 'projscale', 'sn');
[outQN]=SDest(Y,'jpcorr',5,'plots',1,'nsamp',10000, 'projscale', 'qn');

    Input Arguments

    expand all

    Y — Input data. Matrix.

    Data matrix containing n observations on v variables $Y=(y_1^T, ..., y_i^T, ..., y_n^T)^T$.

    $y_i^T$ of size 1-by-v is the ith row of matrix Y.

    Rows of Y represent observations, and columns represent variables.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'nsamp',1000 , 'jpcorr',1 , 'conflev',0.95 , 'margin',2 , 'weight','zch' , 'q',2 , 'c','hdim' , 'nbp',0.6 , 'K',3 , 'nocheck',1 , 'plots',1 , 'msg',1 , 'ysave',1 , 'dirsave',1 , 'rstprojsave',1 , 'projloc',1 , 'projscale',1

    nsamp —Number of random directions.scalar.

    Scalar defining number of random directions which have to be extracted (if not given, default = 1000)

    Example: 'nsamp',1000

    Data Types: single | double

    jpcorr —Subsamples additional size.scalar.

    Integer value greater or equal 0.

    If jpcorr=0 subsamples of size v are extracted. Each subsample gives rise to only 1 direction (called dir).

    If jpcorr=1 subsamples of size v+1 are extracted and they give rise to (v+1) directions.

    If jpcorr = 2, 3, 4, ... subsamples of size v+jpcorr are extracted. We remove the jpcorr-1 units from the subset which have the largest jpcorr-1 Mahalanobis distances so we obtain a subsample of v+1 units which, as before, gives rise to (v+1) directions.

    In the particular case when jpcorr=2 we end up with Juan and Prieto suggestion, that is the unit which has the largest MD is removed from each subsample. The default value of jpcorr is 0.

    Example: 'jpcorr',1

    Data Types: single | double

    conflev —Confidence level which is used to declare units as outliers.scalar.

    Scalar between 0 and 1.

    Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).

    Default value is 0.975.

    Example: 'conflev',0.95

    Data Types: single | double

    margin —Marginal projections.scalar.

    Scalar which specifies if it is necessary to consider marginal projections. Scalar margin specifies up to which order marginal projections must be considered. For example margin = 2 implies that all possible univariate and bivariate marginal projections are considered. Default value is 0 (marginal projections are not considered).

    Remark: note that if margin>0, data are preliminary standardized using medians and MADs.

    Example: 'margin',2

    Data Types: single | double

    weight —Value to use in the weight function.string.

    Value to use in the weight function to transform the outlyingness measure of each observation into a weight.

    Possible values are 'huber', 'tukey', 'zch', and 'mcd'.

    Default is 'mcd'.

    If weight = 'mcd', the [n/2] observations with the smallest distance get weight 1. An asymptotic consistency factor is applied to the estimated covariance matrix.

    If weight = huber, the weights are determined according to the following formula $w(r) = \min(1, (r/c)^{-q})$ with: $c=\min(\sqrt{\chi^2_{v,0.5}},4)$ in Van Aelst, Vandervieren and Willems, "Stahel-Donoho Estimators with Cellwise Weights", (J STAT COMPUT SIM, 2011) (option c='hdim', see below);

    $c=\sqrt{\chi^2_{v,0.95}}$ in Todorov and Filzmoser, "An Object Oriented Framework for Robust Multivariate Analysis", (J OF STAT SOFTWARE, 2009) (option c='sdim', see below);

    q = scalar see below.

    If weight = 'tukey' the Tukey Biweight function is applied, where weights are given by:

    \[ w(r)= \left\{ \begin{array}{c} [1-(r/c)^2]^2 \qquad if \qquad |r| \leq c \\ 0 \qquad \mbox{otherwise} \end{array} \right. \]

    with constant $c$ computed to obtain a prefixed nominal breakdown point (bdp).

    If weight = 'zch', weights are computed according to Zuo, Cui and He's formula (Zuo, Cui and He, "ON THE STAHEL-DONOHO ESTIMATOR AND DEPTH-WEIGHTED MEANS OF MULTIVARIATE DATA", Annals of Statistics (2004)):

    \[ w(PD)= \left\{ \begin{array}{c} (\exp\{-K(1-PD/C)^2\} - \exp\{-K\})/(1-\exp\{-K\}) \qquad\qquad if \qquad PD < c \\ 1 \qquad \mbox{otherwise} \end{array} \right. \]

    where: - $PD$ is the Projection Depth: $PD = 1/(1+r)$ ($r$=outlyingness measure);

    - $C=Median(PD)$;

    - $K$ is a positive tuning parameter.

    Example: 'weight','zch'

    Data Types: char

    q —Constant to be used in the Huber weight function.scalar.

    The default value of q is 2 (see Maronna and Yohai, 1995).

    Example: 'q',2

    Data Types: single | double

    c —Scale parameter.string.

    If c='hdim' (high dimensions) the scale parameter c in the Huber weight function is given by: $c= min(\sqrt{\chi^2_{v,0.5}},4)$. If c='sdim' (small dimensions), parameter c is given by: $c=\sqrt{\chi^2_{v,0.95}}$. The default is 'hdim'.

    Example: 'c','hdim'

    Data Types: char

    nbp —Nominal breakdown point.scalar.

    Nominal breakdown point to be fixed in the Tukey biweight function to obtain the thresold value c (0<nbp<1).

    The default value of npb is 0.5.

    Example: 'nbp',0.6

    Data Types: single | double

    K —Constant to be used in Zuo, Cui and He's family of weights.scalar.

    The default of K is 3.

    Example: 'K',3

    Data Types: single | double

    nocheck —Check input arguments.scalar.

    If nocheck is equal to 1 no check is performed on matrix Y. As default nocheck=0.

    Example: 'nocheck',1

    Data Types: single | double

    plots —Plot on the screen.scalar | structure.

    If plots is a structure or scalar equal to 1, generates: (1) a plot of robust Mahalanobis distances against index number. The confidence level used to draw the confidence bands for the MD is given by the input option conflev. If conflev is not specified a nominal 0.975 confidence interval will be used.

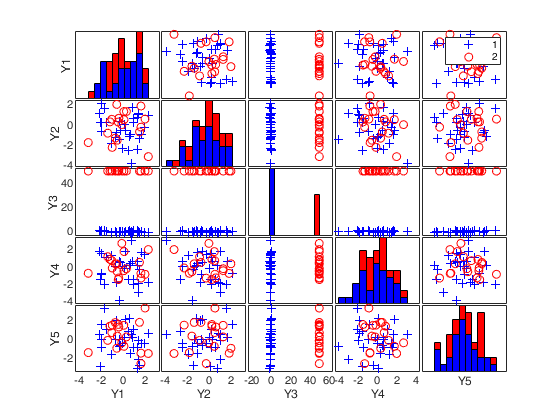
    (2) a scatter plot matrix with the outliers highlighted.

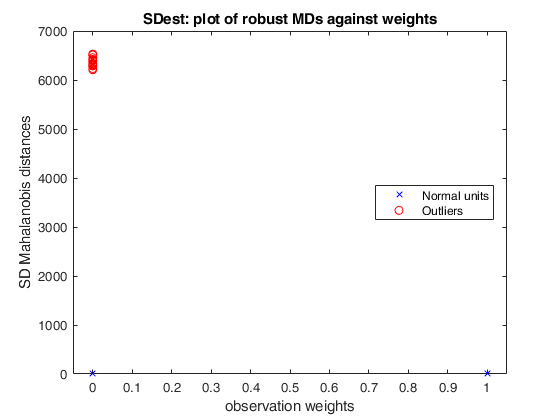
    (3) a scatter plot of robust Mahalanobis distances against observation weights (i.e. the outlyingness measure transformed according to the weight function).

    If plots is a structure it may contain the following fields:

    Value Description
    labeladd

    if this option is '1', the outliers in the spm are labelled with their unit row index. The default value is labeladd='', i.e. no label is added.
    nameY

    cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ...Yv.

    Example: 'plots',1

    Data Types: single | double

    msg —Level of output to display.scalar.

    scalar which controls whether to display or not messages on the screen.

    If msg==1 (default) messages are displayed on the screen about estimated time to compute the final estimator else no message is displayed on the screen.

    Example: 'msg',1

    Data Types: single | double

    ysave —save input matrix Y.scalar.

    Scalar that is set to 1 to request that the data matrix Y is saved into the output structure out. This feature is meant at simplifying the use of function malindexplot.

    Default is 0, i.e. no saving is done.

    Example: 'ysave',1

    Data Types: single | double

    dirsave —save directions.scalar.

    scalar that is set to 1 to request that the all directions for all extracted subsets are saved. If dirsave=1 out structure will contain a field named Dir

    Example: 'dirsave',1

    Data Types: single | double

    rstprojsave —save robust standardized projection scores.scalar.

    Scalar that is set to 1 to request that the robust standardized projection scores associated to each direction are saved for each subset. If projsave=1 out structure will contain a field named RstProj

    Example: 'rstprojsave',1

    Data Types: single | double

    projloc —Type of location.string.

    String with possible values 'median' (default) and 'mean' This option controls the type of location (robust estimator of scale) to use for the projections for each subset. The projections are defined as $d^T \times y_i$ where d is a v-by-1 vector containing a particular direction ($d^T$ is its transpose) (to make estimator location invariant).

    Example: 'projloc',1

    Data Types: single | double

    projscale —Type of standardization.string.

    string with possible values 'mad' (default), 'sn', 'qn' and 'std'.

    This option controls the type of standardization (robust estimator of scale) to use for the centered projections for each subset (to make estimator scale invariant).

    'mad' uses median absolute deviations from the medians (see file mad of statistics toolbox for further details) 'sn' uses a robust version of Gini's average difference (see file Sn of FSDA toolbox for further details) 'qn' uses first quartile of interpoint distances $|x_i-x_j|$ (see file Qn of FSDA toolbox for further details) 'std' uses non robust standard deviations (see file std of statistics toolbox for further details) The two estimators 'sn' and 'qn' have been introduced by Rousseeuw and Croux (1993), JASA, as alternatives to MAD.

    Example: 'projscale',1

    Data Types: single | double

    Output Arguments

    expand all

    out — description Structure

    A structure containing the following fields

    Value Description
    maxdir

    n x v matrix which contains the direction maximizing the robust standardized projection scores for each unit of the sample (that is the direction which produces the outlyingness measure for each observation)
    loc

    1 x v vector containing SD estimate of location
    cov

    v x v matrix containing robust estimate of the covariance matrix
    md

    n x 1 vector containing the estimates of the robust Mahalanobis distances (in squared units)
    outliers

    A vector containing the list of the units declared as outliers using confidence level specified in input scalar conflev
    conflev

    scalar, confidence level that was used to declare outliers
    weights

    n x 1 vector containing the estimates of the weights Weights assume values between 0 and 1.

    If input string weight is 'mcd' the weights are 0 or 1. More precisely the [n/2] associated with the smallest [n/2] measure of outlyingness get weight 1
    Y

    Data matrix Y. This field is present only if option ysave is set to 1.
    Dir

    nsamp-by-v matrix or nsamp-by-v-by-(v+1) array which contains for each subset the direction vectors. More in details, if jpcorr=0 Dirsave is a nsamp-by-v matrix else Dirsave is a 3D array of dimension nsamp-by-v-by-(v+1).

    Remember that in this last case v+1 directions are considered for each subset. This field is present only if option dirsave is set to 1.
    RstProj

    n-by-nsamp matrix or n-by-nsamp-by-(v+1) 3D array which contains the robust standardized projection scores for each unit of the sample for the nsamp projections (or for the nsamp*(v+1) projections if jpcorr>0). The field is present only if option rstprojsave is set to 1.
    class

    'SD'

    varargout —Indices of the subsamples extracted for computing the SD estimate. C : nsamp-by-v+jpcorr matrix

    jpcorr=0,2, 3, ... (see input option jpcorr)

    More About

    expand all

    Additional Details

    A "robust standardized" projection score along direction vector d is defined as follows: $Rstproj_i = \frac{d^T \times y_i -med_j(d^T \times y_j)}{MAD_j(d^T \times y_j)} \;\;\; i=1,\cdots,n$;

    where $med_j(d^T \times y_j)$ and $MAD_j(d^T \times y_j)$ are respectively the median and the modified MAD $j=1,2,\cdots,n$.

    With our two input options projloc and projscale it is possible to use alternative estimators of location and scale to standardize $d^T \times y_i$: $Rstproj_i = \frac{d^T \times y_i -projloc(d^T \times y_j)}{projscale(d^T \times y_j)} \;\;\; i=1,\cdots,n$;

    The outlying measure for unit i ($outl_i$) is defined as: $outl_i = sup_{d \in R^v} (Rstproj_i) \;\;\; i=1, \cdots, n$;

    This outlyingness measure is based on the idea that for any multivariate outlier, one can always find a one-dimensional projection for which the observation is a univariate outlier.

    Remark: note that outl_i(d) = outl_i(c*d) where c is a positive scalar therefore it is not necessary to rescale d to unit norm.

    References

    Stahel, W.A. (1981), "Breakdown of covariance estimators", Research Report 31, Fachgruppe for Statistik, E.T.H. Zurich, Switzerland.

    Donoho, D.L. (1982), "Breakdown Properties of Multivariate Location Estimators", Ph.D. dissertation, Harvard University.

    Maronna, R.A. and Yohai, V.J. (1995), The behavior of the Stahel-Donoho robust multivariate estimator, "Journal of the American Statistical Association", Vol. 90, pp. 329-341.

    Juan J. and Prieto F.J. (1995), "Journal of Computational and Graphical Statistics", Vol. 4, pp. 319-334.

    Maronna, R.A., Martin D. and Yohai V.J. (2006), Robust Statistics, Theory and Methods, Wiley, New York.

    Acknowledgements

    This function follows the lines of MATLAB code developed during the years by many authors.

    See Also

    | | |

    This page has been automatically generated by our routine publishFS