avasmsplot
avasmsplot produces the augmented star plot and enables interactivity
Description
Examples
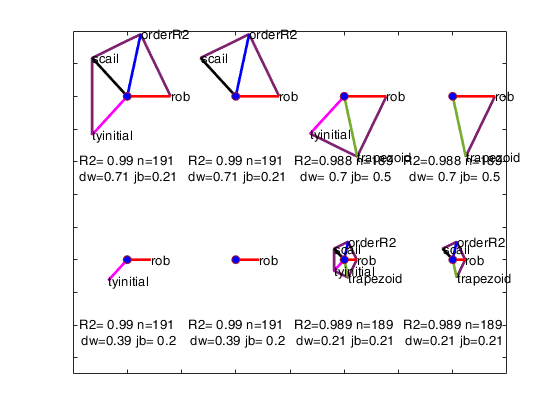
 Example from Wang and Murphy: avasmsplot with all default options.
Example from Wang and Murphy: avasmsplot with all default options.
 Example from Wang and Murphy: avasmsplot with all default options.
Example from Wang and Murphy: avasmsplot with all default options.
close all
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% Show the best solutions
avasmsplot(VALtfin);
 Example of option maxBestSol.
Example of option maxBestSol.
 Example of option maxBestSol.
Example of option maxBestSol.
close all
% Example from Wang and Murphy:
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% Show just the 4 best solutions
avasmsplot(VALtfin,'maxBestSol',4);
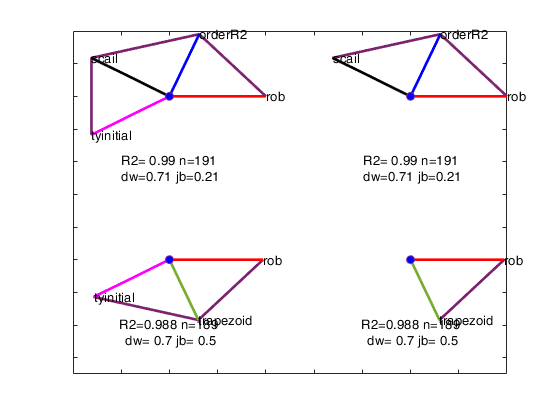
Related Examples
Example of option addPolygons.
close all
% Example from Wang and Murphy:
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% Show just the radial lines and not the polygons around the
% outside of the radial lines
addPolygons=false;
avasmsplot(VALtfin,'maxBestSol',4,'addPolygons',false);
Example of option tag.
close all
% Example from Wang and Murphy:
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% Set a personalized tag
avasmsplot(VALtfin,'tag','mytag');
Interactive example 1.
databrush is passed as a scalar.
% In this case it is possible to brush only once.
close all
% Example from Wang and Murphy:
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% databush is passed as a scalar
% In this case it is possible to brush only once
avasmsplot(VALtfin,'databrush',1)
Interactive example 2.
databrush is passed as a struct.
close all
% Example from Wang and Murphy:
rng('default')
seed=100;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
y([121 80 34 188 137 110 79 86 1])=1.9+randn(9,1)*0.01;
% Automatic model selection
[VALtfin,Resarraychk]=avasms(y,X,'plots',0);
% databrush is passed as a struct
databrush=struct;
databrush.persist='on';
databrush.BrushShape='rect';
databrush.BrushSize=0.2;
avasmsplot(VALtfin,'databrush',databrush)
Input Arguments
BestSol — Best solutions.
table.
A table containing the details of the admissible solutions which have been found. We define a solution as admissible if the residuals pass the Durbin-Watson and Jarque-Bera tests, at the 10 per cent level.
If no solution is found, than a 5 per cent threshold for both tests is used.
Note that in input option critBestSol it is possible to set up different thresholds to define the admissible solutions.
The rows of BestSol are ordered in a non increasing way using the p-value of the Durbin Watson test (rescaled by the value of and the number of units not declared as outliers).
Colums 1-5 contain boolean information about the usage of options: orderR2, scail, trapezoid, rob, tyinitial. These 5 columns are ordered in non decreasing way depending on the frequency in which a particular option has been used in the set of admissiable solutions.
For example, if option orderR2 is the only one which is always used in the set of admissible solutions, then column 1 is associated to orderR2.
6th column contains the value of R2 (column name R2).
7th column contains the p-value of Durbin Watson test (column name pvalDW).
8th column contains the p-value of Jarque Bera test (column name pvalJB).
9th column contains the number of units which have not been declared as outliers (column name nused).
10th column is a cell which contains the residuals for the associated solution.
11th column contains the struct out which is the output of the call to avas.
12th column contains the numbers obtained by the product of p-value of Durbin Watson test, the values of R^2 and the number of units which have not been declared as outliers. The values of this column depend on the optional input argument solOrdering.
Data Types: table
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'maxBestSol',5
, 'showBars',true
, 'addPolygons',false
, 'corMatrix',eye(p)
, 'tag','myplot'
, 'databrush',1
maxBestSol
—maximum number of admissible
solutions to show in the augmented star plot.missing | positive integer.
if maxBestSol is missing all solutions inside input table BestSol are shown in the augmented star plot.
If maxBestSol is (say) 3, just the first 3 solutions are shown in in the augmented star plot.
Example: 'maxBestSol',5
Data Types: double
showBars
—show bars of labels.boolean.
If showBars is true the values of R2, fraction of units used, pvalue of DW test and pval of normality test are shown with bars below each star, else (default) these values are shows using a textbox. More precisely, If k is the total number of units declared as outliers the four bars represent respectively R^2, (n − 2k)/n, p_{DW} and p_{JB}. Note that we have 2k rather than k because the maximum number of outliers is [n/2].
Example: 'showBars',true
Data Types: logical
addPolygons
—polygons around the outside.boolean.
if addPolygons is true (default) , polygons around the outside of the radial lines are added to the augmented star plot. If addPolygons is false just the radial lines from the center are shows.
Example: 'addPolygons',false
Data Types: logical
corMatrix
—correlation matrix among the input solutions.array of size maxBestSol-by-maxBestSol | [] (default).
If this optional argument is supplied it is possible to have in output the heatmap among the different solutions. The correlation matrix is returned as second output of function avasmsplot.
If corMatrix is an empty value (default) just the augmented star plot is shown on the screen.
Example: 'corMatrix',eye(p)
Data Types: double
tag
—Personalized plot tag.string.
String which identifies the handle of the plot which is about to be created. The default is to use tag 'pl_augstarplot'. Note that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created.
Example: 'tag','myplot'
Data Types: char
databrush
—interactive mouse brushing.empty value, scalar | structure.
If databrush is an empty value (default), no brushing is done. The activation of this option (databrush is a scalar or a struct) enables the user to select a set of solutions in the current plot and to see them shown in the aceplot (i.e. a plot which enables to visualize the results of avas).
DATABRUSH IS A SCALAR If databrush is a scalar the default selection tool is a circular brush and it is possible to brush only once (that is persist='').
DATABRUSH IS A STRUCTURE.
If databrush is a structure, it is possible to use all optional arguments of function selectdataFS and the following optional argument: - persist. Persist is an empty value or a scalar containing the strings 'on' or 'off'.
The default value of persist is '', that is brushing is allowed only once.
If persist is 'on' or 'off' brushing can be done as many time as the user requires.
If persist='on' then the aceplot for the solution(s) currently brushed are added to those previously brushed.
If persist='off' every time a new brush is performed the aceplot containing previous solutions is removed.
Example: 'databrush',1
Data Types: single | double | struct
Output Arguments
BigAx —handle to big (invisible) axes framing the subaxes.
Graphical handle
BigAx is left as the CurrentAxes so that a subsequent TITLE, XLABEL, or YLABEL will be centered with respect to the matrix of axes.
References
Riani M. and Atkinson A.C. and Corbellini A. (2023), Robust Transformations for Multiple Regression via Additivity and Variance Stabilization, submitted.

|
avasms |
balloonplot |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments