avas
avas computes additivity and variance stabilization for regression
Description
Examples
 Example of the use of avas based on the Wang and Murphy data.
Example of the use of avas based on the Wang and Murphy data.
 Example of the use of avas based on the Wang and Murphy data.
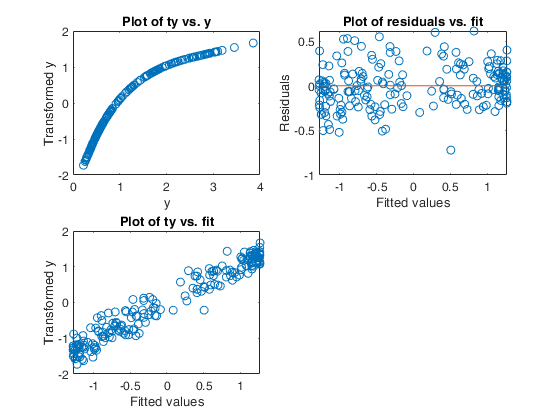
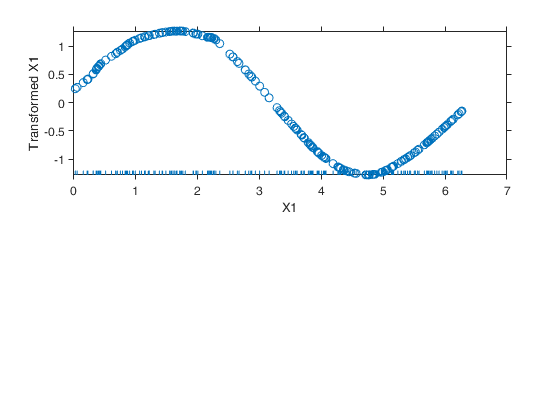
Example of the use of avas based on the Wang and Murphy data.In order to have the possibility of replicating the results in R using library acepack function mtR is used to generate the random data.
rng('default')
seed=11;
negstate=-30;
n=200;
X1 = mtR(n,0,seed)*2-1;
X2 = mtR(n,0,negstate)*2-1;
X3 = mtR(n,0,negstate)*2-1;
X4 = mtR(n,0,negstate)*2-1;
res=mtR(n,1,negstate);
% Generate y
y = log(4 + sin(3*X1) + abs(X2) + X3.^2 + X4 + .1*res );
X = [X1 X2 X3 X4];
% Apply the avas algorithm
out= avas(y,X);
% Show the output graphically using function aceplot
aceplot(out)
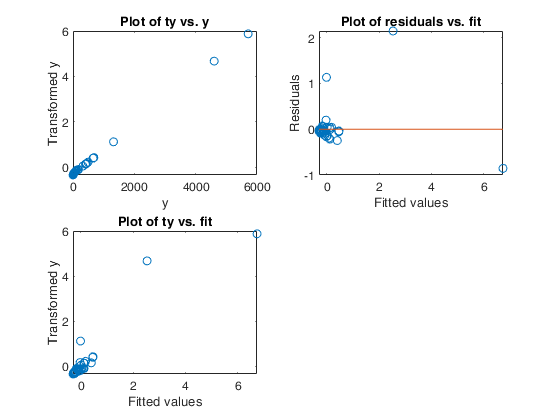
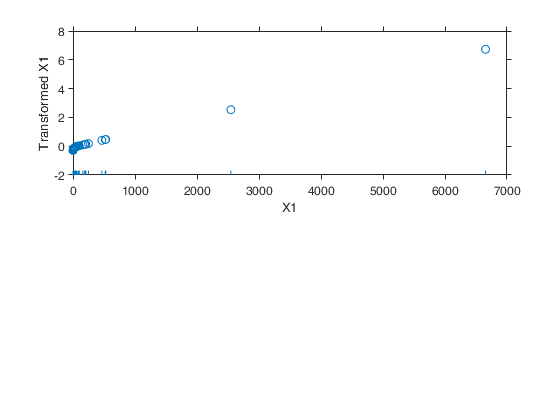
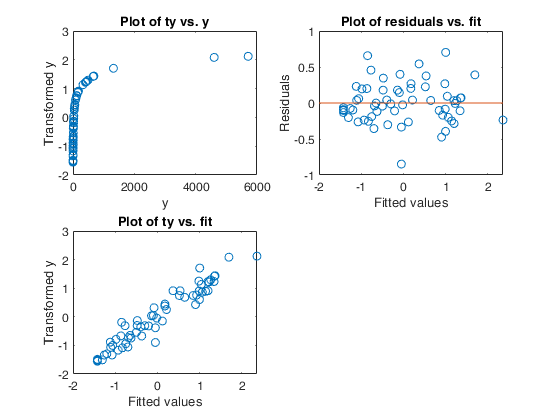
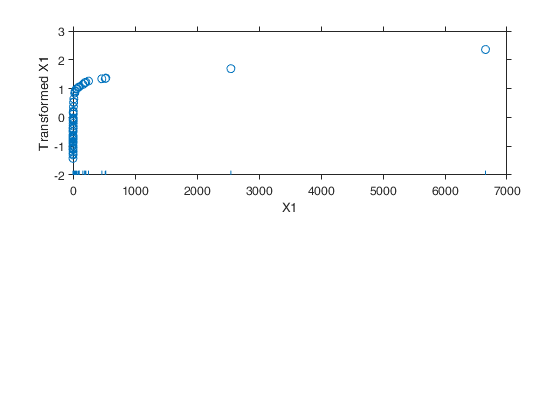
 Example 1 from TIB88: brain body weight data.
Example 1 from TIB88: brain body weight data.
 Example 1 from TIB88: brain body weight data.
Example 1 from TIB88: brain body weight data.Comparison between ace and avas.
YY=load('animals.txt');
y=YY(1:62,2);
X=YY(1:62,1);
out=ace(y,X);
aceplot(out)
out=avas(y,X);
aceplot(out)
% https://vincentarelbundock.github.io/Rdatasets/doc/robustbase/Animals2.html
% ## The `same' plot for Rousseeuw's subset:
% data(Animals, package = "MASS")
% brain <- Animals[c(1:24, 26:25, 27:28),]
% plotbb(bbdat = brain)
Related Examples
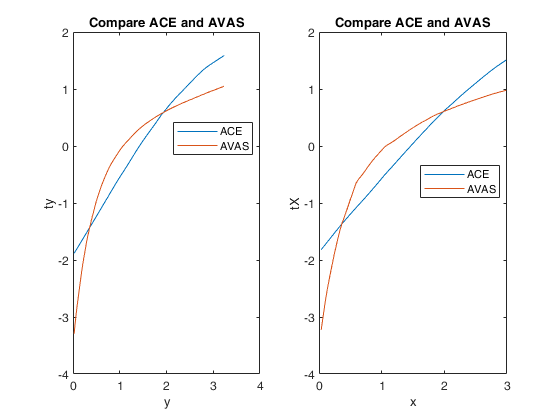
 Example 3 from TIB88: unequal variances.
Example 3 from TIB88: unequal variances.
 Example 3 from TIB88: unequal variances.
Example 3 from TIB88: unequal variances.
n=200;
rng('default')
seed=100;
negstate=-30;
x = mtR(n,0,seed)*3;
z = mtR(n,1,negstate);
y=x+0.1*x.*z;
X=x;
nr=1;
nc=2;
outACE=ace(y,X);
outAVAS=avas(y,X);
subplot(nr,nc,1)
yy=[y, outACE.ty outAVAS.ty];
yysor=sortrows(yy,1);
plot(yysor(:,1),yysor(:,2:3))
% plot(y,[outACE.ty outAVAS.ty])
title('Compare ACE and AVAS')
xlabel('y')
ylabel('ty')
legend({'ACE' 'AVAS'},'Location','Best')
subplot(nr,nc,2)
XX=[X, outACE.tX outAVAS.tX];
XXsor=sortrows(XX,1);
plot(XXsor(:,1),XXsor(:,2:3))
% plot(y,[outACE.ty outAVAS.ty])
title('Compare ACE and AVAS')
xlabel('x')
ylabel('tX')
legend({'ACE' 'AVAS'},'Location','Best')
% For R users, the R code to reproduce the example above is given
% below.
% set.seed(100)
% n=200
% x <- runif(n)*3
% z <- rnorm(n)
% y=x+0.1*x*z;
% out=ace(x,y)
% out=avas(x,y)
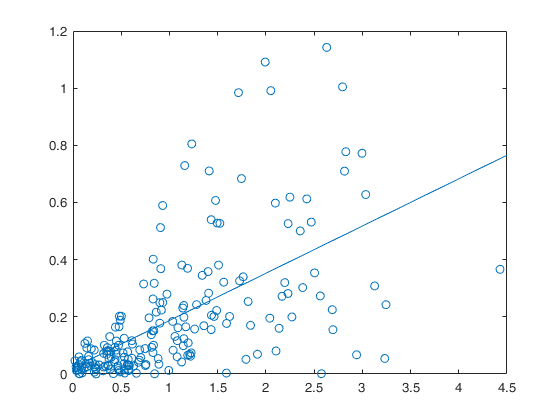
 Example 4 from TIB88: non constant underlying variance.
Example 4 from TIB88: non constant underlying variance.
 Example 4 from TIB88: non constant underlying variance.
Example 4 from TIB88: non constant underlying variance.
close all
negstate=-100;
rng('default')
seed=100;
n=200;
x1=mtR(n,1,seed);
x2=mtR(n,1,negstate);
z=mtR(n,1,negstate);
% x1=randn(n,1);
% x2=randn(n,1);
% z=randn(n,1);
absx1_x2=abs(x1-x2);
y=x1+x2+(1/3)*absx1_x2.*z;
X=[x1 x2];
out=avas(y,X);
tyhat=sum(out.tX,2);
ty=out.ty;
absty_tyhat=abs(ty-tyhat);
% hold('on')
plot(absx1_x2,absty_tyhat,'o');
lsline
% For R users, the R code to reproduce the example above is given
% below.
% # Example 4 non constant underlying variance
% set.seed(100)
% n=200;
% x1=rnorm(n);
% x2=rnorm(n);
% z=rnorm(n);
% absx1_x2=abs(x1-x2);
% y=x1+x2+(1/3)*absx1_x2*z;
% X=cbind(x1,x2);
% out=avas(X,y);
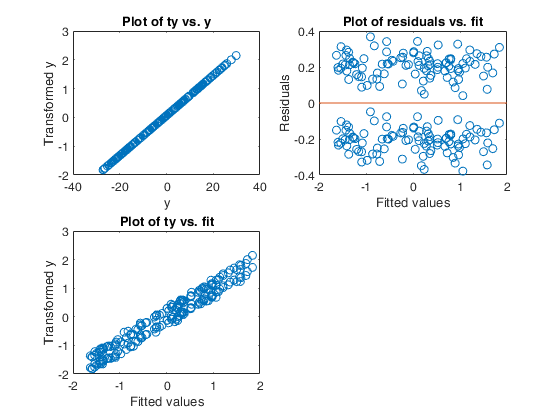
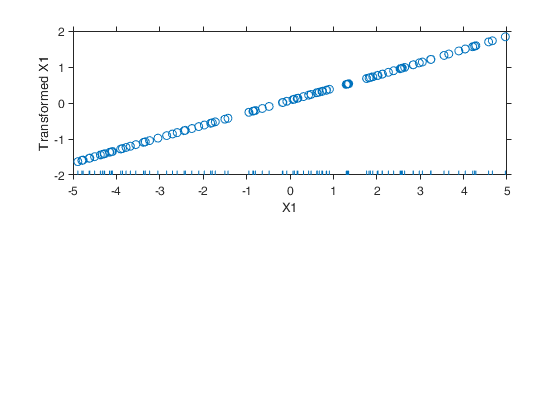
 Example 5 from TIB88: missing group variable.
Example 5 from TIB88: missing group variable.
 Example 5 from TIB88: missing group variable.
Example 5 from TIB88: missing group variable.
rng('default')
seed=1000;
n=100;
x=mtR(n,0,seed)*10-5;
z=mtR(n,1,-seed);
%x=rand(n,1)*10-5;
%z=randn(n,1);
y1=3+5*x+z;
y2=-3+5*x+z;
y=[y1;y2];
X=[x;x];
out=avas(y,X);
aceplot(out);
% For R users, the R code to reproduce the example above is given
% below.
% # Example 5 missing group variable
% set.seed(1000)
% n=100;
% x=runif(n)*10-5;
% z=rnorm(n);
% y1=3+5*x+z;
% y2=-3+5*x+z;
% y=c(y1,y2);
% X=c(x,x)
% out=avas(X,y);
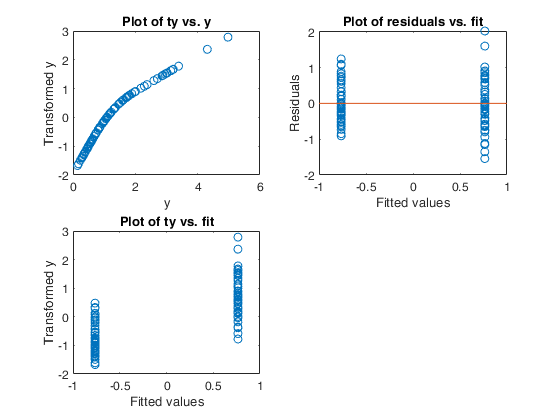
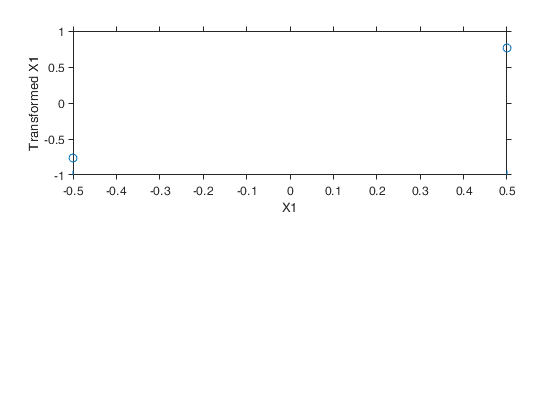
 Example 6 from TIB88: binary.
Example 6 from TIB88: binary.
 Example 6 from TIB88: binary.
Example 6 from TIB88: binary.
seed=20;
n=50;
y1=exp(-0.5+0.5*mtR(n,1,seed));
y2=exp(0.5+0.5*mtR(n,1,-seed));
y=[y1;y2];
X=[-0.5*ones(n,1); 0.5*ones(n,1)];
out=avas(y,X);
aceplot(out)
% For R users, the R code to reproduce the example above is given
% below.
% Example 6 binary
% set.seed(20)
% n=50;
% y1=exp(-0.5+0.5*rnorm(n));
% y2=exp(0.5+0.5*rnorm(n));
% y=c(y1,y2);
% X=c(-0.5*rep(1,n), 0.5*rep(1,n));
% out=avas(X,y);
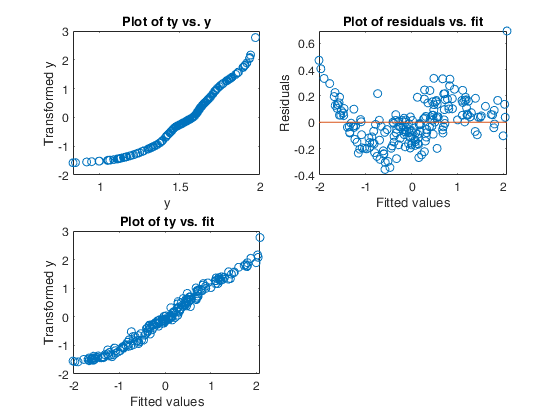
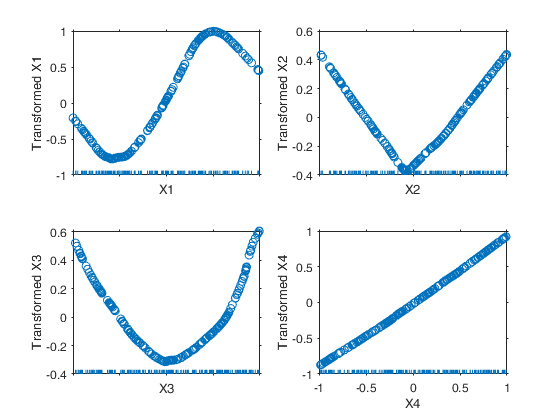
Example of use of option tyinitial.
Generate the data.
rng(2000)
n=100;
X=10*rand(n,1);
sigma=0.1;
a=2;
b=0.3;
y=a+b*X+sigma*randn(n,1);
% The correct transformation is la=-0.5 (inverse square root)
la=-0.5;
y=normBoxCox(y,1,la,'inverse',true);
% call of AVAS without option tyinitial
subplot(2,1,1)
outAVAS=avas(y,X,'l',4);
tyfinal=outAVAS.ty;
out=fitlm(X,tyfinal);
plot(X,tyfinal,'o')
lsline
xlabel('Original x')
ylabel('Without option tyinitial')
title(['R2=' num2str(out.Rsquared.Ordinary)])
% call of AVAS with option tyinitial set to true
subplot(2,1,2)
outAVAStyini=avas(y,X,'l',4,'tyinitial',true);
tyfinal=outAVAStyini.ty;
out=fitlm(X,tyfinal);
plot(X,tyfinal,'o')
lsline
xlabel('Original x')
ylabel('With option tyinitial')
title(['R2=' num2str(out.Rsquared.Ordinary)])
Input Arguments
y — Response variable.
Vector.
Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single| double
X — Predictor variables.
Matrix.
Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.
Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'delrsq',0.001
, 'l',[3 3 1]
, 'maxit',30
, 'nterm',5
, 'orderR2',true
, 'rob',true
, 'scail',true
, 'trapezoid',true
, 'tyinitial',true
, 'w',1:n
delrsq
—termination threshold.scalar.
Iteration (in the outer loop) stops when rsq changes less than delrsq in nterm. The default value of delrsq is 0.01.
Example: 'delrsq',0.001
Data Types: double
l
—type of transformation.vector.
Vector of length p which specifies the type of transformation for the explanatory variables.
l(j)=1 => j-th variable assumes orderable values and any transformation (also non monotone) is allowed.
l(j)=2 => j-th variable assumes circular (periodic) values in the range (0.0,1.0) with period 1.0.
l(j)=3 => j-th variable transformation is to be monotone.
l(j)=4 => j-th variable transformation is to be linear.
l(j)=5 => j-th variable assumes categorical (unorderable) values.
j =1, 2,..., p.
The default value of l is a vector of ones of length p, this procedure assumes that all the explanatory variables have orderable values (and therefore can be transformed non monotonically).
Note that in avas procedure the response is always transformed (in a monotonic way).
Example: 'l',[3 3 1]
Data Types: double
maxit
—maximum number of iterations for the outer loop.scalar.
The default maximum number of iterations before exiting the outer loop is 20.
Example: 'maxit',30
Data Types: double
nterm
—minimum number of consecutive iteration below the threshold
to terminate the outer loop.positive scalar.
This value specifies how many consecutive iterations below the threshold it is necessary to have to declare convergence in the outer loop. The default value of nterm is 3.
Example: 'nterm',5
Data Types: double
orderR2
—inclusion of the variables using .boolean.
The default backfitting algorithm of AVAS (orderR2=false) just does one iteration over the predictors, it may not find optimal transformations and it will be dependent on the order of the predictors in X. If orderR2=true, in the backfitting algorithm the explanatory variables become candidate for transformation depending on their R^2 order of importance. The default value of orderR2 is false.
Example: 'orderR2',true
Data Types: logical
rob
—Use outlier detection in each step of the backfitting procedure.boolean | struct.
If rob is not specified, rob is set to false and no outlier detection routine is called.
If rob is true, FSR routine is called to detect outliers before calling backfitting procedure and outliers are removed.
If rob is a struct, it is possible to specify in the fields method, bdp and alphasim the values of the estimator to use, the breakdown point and and confidence level to use to declare the outliers.
More precisely:
| Value | Description |
|---|---|
method |
character which identifies the estimator to use. Possible values are 'FS' (Forward search estimator', 'LTS' (Least trimmed squares estimator), 'LMS' (Least median of squares), 'S' (S estimator). If this field is not specified 'FS' is used. |
bdp |
a scalar in the interval (0, 0.5] which specifies breakdown point to use. If this field is not specified it is set to 0.2. |
simalpha |
simultaneous error rate one is willing to tolerate to declare the outliers. If rob.simalpha is not specified it is set to 0.01. |
Example: 'rob',true
Data Types: boolean or struct
scail
—Initializing values for the regressors.boolean.
If scail is true (default value is false), a linear regression is done on the independent variables X_1, ...X_{p-1} centered, using y standardized, getting the coefficients b_1, ..., b_{p-1}.
If scail is true, AVAS takes the initial value of the transformation of X_j to be b_j(X_j-mean(X_j)), j=1, \ldots, p-1. This is done in order to limit the effect of the ordering of the variables on the final results. The purpose of this initial linear transformation is to let the the columns of matrix X have the same weight when predicting y.
Note that this initialization option is always used inside the ACE routine but it is set to false in AVAS or compatibility with the original fortran program of Tibshirani.
See the ADDED NOTE in the [Monotone Regression Splines in Action]: Comment. Leo Breiman Statistical Science, Vol. 3, No.
4 (Nov., 1988), pp. 442-445.
Example: 'scail',true
Data Types: logical
trapezoid
—strategy for evaluating points that lie outside the
domain of fitted values inside the routine which computes the
variance stabilizing transformation (ctsub).boolean.
This options specifies the hypothesis to assume in the cases in which \widehat{ty}_i^{old}<\hat y_{(1)} or \widehat{ty}^{old}>\hat y_{n-k} where \hat y_{(1)}, ..., \hat y_{(n-k)} are the fitted values sorted of the n-k units which have not been declared as outliers and \widehat{ty}_i^{old} is the transformed value for unit i from previous iteration (i=1, \ldots, n).
If this option is omitted or if trapezoid is false (default), we assume a rectangular hypothesis. In other words, we assume that below \hat y_{(1)} the function 1/|e_1|, \ldots, 1/|e_{n-k}|, is constant and equal to 1/|e_1|, |e_1|, \ldots, |e_{n-k}| are the smoothed residuals corresponding to ordered fitted values.
Similarly, we assume that beyond \hat y_{n-k} the function is constant and equal to 1/|e_{n-k}|. If trapezoid is false we assume that below \hat y_{(1)} or above \hat y_{(n-k)} the function is constant and equal to the mean of \sum_{j=1}^{n-k} 1/(|e_j| (n-k)) (trapezoidal hypothesis).
Additional details are given in the More About section of this file.
Example: 'trapezoid',true
Data Types: logical
tyinitial
—Initial values for the transformed response.boolean | struct.
If tyinitial is not specified, tyinitial is set to false and the initial value for ty are simply the standardized values.
If tyinitial is true, y is transformed using best BoxCox lambda value among the following values of lambda (-1, -0.8, -0.6, ..., 0.8, 1) and routines FSRfan and fanBIC are called.
If tyinitial is a struct it is possible to specify in the fields la and family, the values of lambda and the family to use. More precisely:
| Value | Description |
|---|---|
la |
values of the lambdas to consider inside FSRfan. |
family |
string which identifies the family of transformations which must be used. Character. Possible values are 'BoxCox' (default), 'YJ', or 'YJpn'. The Box-Cox family of power transformations equals (y^{\lambda}-1)/\lambda for \lambda not equal to zero, and \log(y) if \lambda = 0. The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of y+1 for nonnegative values, and of |y|+1 with parameter 2-\lambda for y negative. Remember that BoxCox can be used just if input y is positive. Yeo-Johnson family of transformations does not have this limitation. If family is 'YJpn' Yeo-Johnson family is applied but in this case it is also possible to monitor (in the output arguments out.Scorep and out.Scoren) the score test respectively for positive and negative observations. |
Example: 'tyinitial',true
Data Types: boolean or struct
w
—weights for the observations.vector.
Row or column vector of length n containing the weights associated to each observations. If w is not specified we assume w=1 for i=1, 2, \ldots, n.
Example: 'w',1:n
Data Types: double
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
ty |
n x 1 vector containing the transformed y values. |
tX |
n x p matrix containing the transformed X matrix. |
rsq |
the multiple R-squared value for the transformed values in the last iteration of the outer loop. |
y |
n x 1 vector containing the original y values. |
X |
n x p matrix containing the original X matrix. |
niter |
scalar. Number of iterations which have been necessary to achieve convergence. |
outliers |
k x 1 vector containing the units declared as outliers when procedure is called with input option rob set to true. If rob is false out.outliers=[]. |
pvaldw |
scalar containing p-value of Durbin Watson test for the independence of the residuals ordered by the fitted values from the model. |
pvaljb |
scalar containing p-value of Jarque and Bera test. This statistic uses a combination of estimated skewness and kurtosis to test for distributional shape of the residuals. |
More About
Additional Details
In what follows we recall the technique of the variance stabilizing transformation which is at the root of the avas routine.
Let X be a random variable, with E[X]=\mu and \mathrm{Var}[X]=\sigma^2 .
Define Y=g(X) , where g is a regular function. A first-order Taylor approximation for Y=g(x) is
Y=g(X)\approx g(\mu)+g'(\mu)(X-\mu). Then E[Y]=g(\mu)\; \mbox{and} \; \mathrm{Var}[Y]=\sigma^2g'(\mu)^2.Consider now a random variable X such that E[X]=\mu and \mathrm{Var}[X]=h(\mu) . Notice the relation between the variance and the mean, which implies, for example, heteroskedasticity in a linear model. The goal is to find a function g such that Y=g(X) has a variance independent (at least approximately) of its expectation.
Imposing the condition \mathrm{Var}[Y]\approx h(\mu)g'(\mu)^2=\mathrm{constant} , equality implies the differential equation
\frac{dg}{d\mu}=\frac{C}{\sqrt{h(\mu)}}. This ordinary differential equation has, by separation of variables, the solution g(\mu)=\int \frac{Cd\mu}{\sqrt{h(\mu)}}. Tibshirani (JASA, p.395) has a random variable W with E[W]=u and \mathrm{Var}[W]=v(u). The variance stabilizing transformation for W is given by h(t)=\int^t \frac{1}{\sqrt{v(u)}}.The constant C = 1 due to the standardization of the variance of W.
In our context \frac{1}{\sqrt{v(u)}} corresponds to vector of the reciprocal of the absolute values of the smoothed residuals sorted using the ordering based on fitted values of the regression model which uses the explanatory variables possibly transformed. The x coordinates of the function to integrate are the fitted values sorted.
As concerns the range of integration it goes from \hat y_{(1)} the smallest fitted value, to \widehat{ty}_i^{old}.
Therefore the lower extreme of integration is fixed for all n integrals.
The upper extremes of integration are given by the elements of transformed response values from previous iteration (say \widehat{ty}_i^{old}), corresponding to ordered fitted values.
The output of the integration is a new set of transformed values \widehat{ty}^{new}.
In summary, the trick is that, there is not just one integral, but there are n integrals. Th i-th integral which is defined as
\widehat{ty}_i^{new}= \int_{\hat y_{(1)}}^{\widehat{ty}_i^{old}} \frac{1}{|e_i|} d \hat yproduces a new updated value for the transformed response \widehat{ty}_i associated with \hat y_{(i)} the i-th ordered fitted value. Note that the old transformed value from previous iteration was the upper extreme of integration.
The estimate of g is strictly increasing because it is the integral of a positive function (reciprocal of the absolute values of the residuals).
The computation of the n integrals is done by the trapezoidal rule and is detailed in routine ctsub.
{\it Remark}: It may happen that at a particular iteration of the AVAS procedure using \widehat{ty} and \widehat{tX}, n-m units are declared as outliers. In this case the fit, the residuals and the associated smoothed values are computed using just n-k observations.
Therefore the function to integrate has coordinates
(\hat y_{(1)}, 1/|e_1|) , (\hat y_{(2)}, 1/|e_2|), \ldots, (\hat y_{(n-k)}, 1/|e_{n-k}|)where \hat y_{(j)} is the j-th order statistic j=1, 2, \ldots, n-k among the fitted values (associated to non outlying observations) and 1/e_j is the reciprocal of the corresponding smoothed residual. Notice that e_j is not the residual for unit j but it is the residual which corresponds to the j-th ordered fitted value \hat y_{(j)}. In order to have a new estimate of \widehat{ty}^{new}, we can still solve n integrals. If in the upper extreme of integration, we plug in the n old values of \widehat{ty}^{old} (including the outliers) we have the vector of length n of the new estimates of transformed values \widehat{ty}^{new}.
References
Tibshirani R. (1987), Estimating optimal transformations for regression, "Journal of the American Statistical Association", Vol. 83, 394-405.
Wang D. and Murphy M. (2005), Identifying nonlinear relationships regression using the ACE algorithm, "Journal of Applied Statistics", Vol. 32, pp. 243-258.