Response variable, specified as
a vector of length n, where n is the number of
observations. Each entry in y is the response for the
corresponding row of X.
Missing values (NaN's) and infinite values (Inf's) are
allowed, since observations (rows) with missing or infinite
values will automatically be excluded from the
computations.
Data Types: single| double
Matrix of explanatory
variables (also called 'regressors') of dimension n x (p-1)
where p denotes the number of explanatory variables
including the intercept.
Rows of X represent observations, and columns represent
variables. By default, there is a constant term in the
model, unless you explicitly remove it using input option
intercept, so do not include a column of 1s in X. Missing
values (NaN's) and infinite values (Inf's) are allowed,
since observations (rows) with missing or infinite values
will automatically be excluded from the computations.
Data Types: single| double
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
Example:
'l',[3 3 1]
, 'w',1:n
, 'nterm',5
, 'delrsq',0.001
, 'maxit',30
Vector of length p+1 which
specifies how the type of transformation for the explanatory
variables and the response. The first p element of this vector
refers to the p explanatory variables, the last element refers to
the response.
l(j)=1 => j-th variable assumes orderable values.
l(j)=2 => j-th variable assumes circular (periodic) values
in the range (0.0,1.0) with period 1.0.
l(j)=3 => j-th variable transformation is to be monotone.
l(j)=4 => j-th variable transformation is to be linear.
l(j)=5 => j-th variable assumes categorical (unorderable) values.
j =1, 2, \ldots, p+1.
The default value of l is a vector of ones of length p+1,
this procedure assumes that both the explanatory
variables and the response have orderable values.
Example: 'l',[3 3 1]
Data Types: double
Row or column vector of
length n containing the weights associated to each
observations. If w is not specified we assume for i=1,
2, \ldots, n.
Example: 'w',1:n
Data Types: double
This value
specifies how many consecutive iterations below the threshold
it is necessary to have to declare convergence in the outer
loop. The default value of nterm is 3.
Example: 'nterm',5
Data Types: double
Iteration (in the outer loop)
stops when rsq changes less than delrsq in nterm. The default
value of delrsq is 0.01.
Example: 'delrsq',0.001
Data Types: double
The
default maximum number of iterations before exiting the outer
loop is 20.
Example: 'maxit',30
Data Types: double


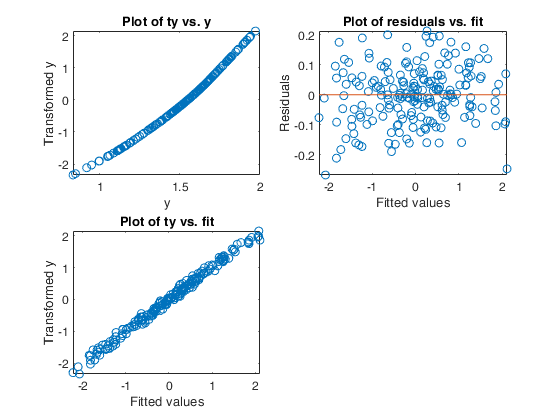
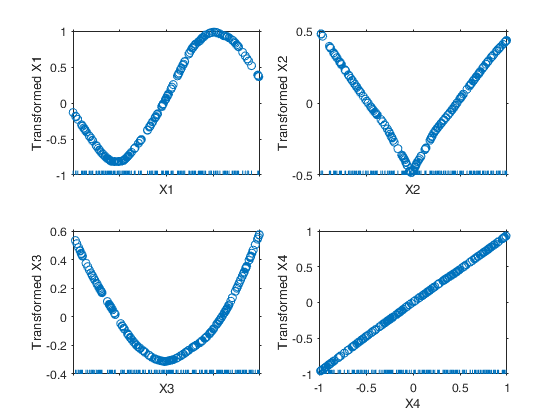
 Example of the use of ace based on the Wang and Murphy data.
Example of the use of ace based on the Wang and Murphy data.