Scalar that
specifies the type of transformation.
l=1 => transformation can also be non monotone. In this case,
the supersmoother is initially applied. In presence of
equal values of x, the unweighted arithmetic mean of the
smoothed values is returned.
l=2 => j-th variable assumes circular (periodic) values
in the range (0.0,1.0) with period 1.0.
l=3 => transformation is to be monotone. In this case, the
supersmoother is initially applied. Monotonic
transformation is forced applying isotonic regression to
(1) the output of the supersmoother and to the flipped
upside down (2) output of the supersmoother. The choice
between solution (1) and (2) is made based on the output
that is closest to the output of the supersmoother.
Closeness is measured in terms of sum
of squares of residuals. Equal consecutive values
smoothed values are replaced by linearly interpolated values.
In presence of equal values of x, the unweighted
arithmetic mean of the final smoothed values is
returned.
l=4 => transformation is to be linear. In this case, the smoothed
values are simply the fitted values from least squares
fit.
l=5 => the predictor variable is categorical. In this case, the smoothed
values are simply the (weighted) values of y in
correspondence of each value of x.
Data Types: single| double
Ordered abscissa values.
Note that the x values are assumed non decreasing.
Data Types: single| double
Response variable that has to
be smoothed, specified as
a vector of length n, where n is the number of
observations.
Data Types: single| double
Row or column vector of
length n containing the weights associated to each
observations. If w is not specified, we assume: for i=1,
2, \ldots, n.
Example: 'w',1:n
Data Types: double
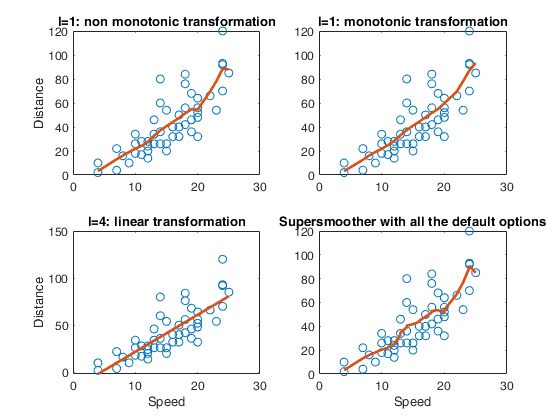
 Compare 4 different smoothers.
Compare 4 different smoothers.