The supersmoother algorithm computes three separate smooth curves from
the input data with symmetric spans of 0.05*n, 0.2*n, and 0.5*n, where n
is the number of data points. The best of the three smooth curves is
chosen for each predicted point using leave-one-out cross validation. The
best spans are then smoothed by a fixed-span smoother (span = 0.2*n), and
the prediction is computed by linearly interpolating between the three
smooth curves. This final smooth curve is then smoothed again with a
fixed-span smoother (span = 0.05*n).
According to comments by Friedman, "for small samples (n < 40) or if
there are substantial serial correlations between observations close in
x-value, then a prespecified fixed span smoother (span > 0) should be
used. Reasonable span values are 0.2 to 0.4."
This function is basically equal to the
function supsmu written in MALTAB by Douglas M. Schwarz.
Email: dmschwarz=ieee*org, dmschwarz=urgrad*rochester*edu
Real_email = regexprep(Email,{'=','*'},{'@','.'})
The following modifications with respect to the original function have
been made:
[
1] In case of constant values of x over a span program was producing
NA. Modifications have been done in the subroutines to cope with this
case.
[
2] The formula for the cross validation residuals in presence of
constant values has been introduced.
[
3] All the Mlint suggestions have been incorporated.
[
4] The help has been put inside the FSDA style.
[
5] A series of examples that explore the different options have been
added.
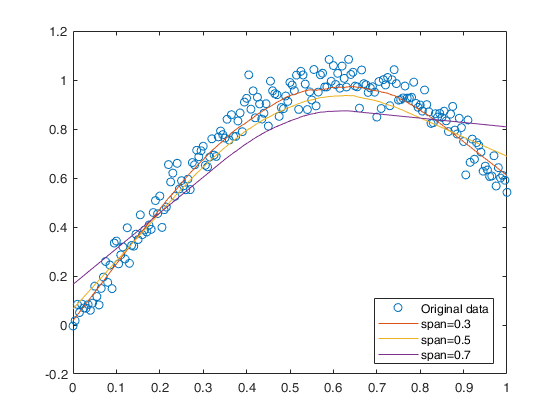
 An example of the use of the option Span.
An example of the use of the option Span.