smothr

smothr produces smoothed values with constraints.

expand all in page

Syntax

Description

This function is used in each step of the iterative procedure for ACE, but can be called directly when it is necessary to smooth a set of values. Note that the x values must be non decreasing.

example

ysmo =smothr(l, x, y) Compare 4 different smoothers.

example

ysmo =smothr(l, x, y, w) An example where the predicted variable is categorical.

Examples

expand all

  • Compare 4 different smoothers.

    • The data give the speed of cars and the distances taken to stop. Note that the data were recorded in the 1920s. 

    % The first column of X is speed, while the second is the time to stop.
X=[ 4    2
4   10
7    4
7   22
8   16
9   10
10   18
10   26
10   34
11   17
11   28
12   14
12   20
12   24
12   28
13   26
13   34
13   34
13   46
14   26
14   36
14   60
14   80
15   20
15   26
15   54
16   32
16   40
17   32
17   40
17   50
18   42
18   56
18   76
18   84
19   36
19   46
19   68
20   32
20   48
20   52
20   56
20   64
22   66
23   54
24   70
24   92
24   93
24  120
25   85];
x=X(:,1);
y=X(:,2);
% Compare the output.
subplot(2,2,1)
% Non monotonic output l=1.
plot(x,y,'o')
hold('on')
l=1;
ysmo=smothr(l,x,y);
plot(x,ysmo,'-','LineWidth',2)
title('l=1: non monotonic transformation')
ylabel('Distance')
subplot(2,2,2)
% Impose monotonic output.
% Input option l=3.
plot(x,y,'o')
hold('on')
l=3;
ysmo=smothr(l,x,y);
plot(x,ysmo,'-','LineWidth',2)
title('l=1: monotonic transformation')
subplot(2,2,3)
% Impose monotonic output.
% Input option l=4.
plot(x,y,'o')
hold('on')
l=4; 
% Impose a linear smoother
ysmo=smothr(l,x,y);
plot(x,ysmo,'-','LineWidth',2)
title('l=4: linear transformation')
xlabel('Speed')
ylabel('Distance')
subplot(2,2,4)
% Impose monotonic output
plot(x,y,'o')
hold('on')
ysmo=supsmu(x,y);
plot(x,ysmo,'-','LineWidth',2)
title('Supersmoother with all the default options')
xlabel('Speed')
ylabel('Distance')
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • An example where the predicted variable is categorical.

    • seed=20;
n=5;
y1=exp(-0.5+0.5*mtR(n,1,seed));
y2=exp(0.5+0.5*mtR(n,1,-seed));
y=[y1;y2];
X=[-0.5*ones(n,1); 0.5*ones(n,1)];
X(9:10)=1;
ysmo=smothr(5,X,y);
plot(X,y,'o')
hold('on')
plot(X,ysmo)
xlabel('Variable with 3 levels')
ylabel('Original and smoothed y values')

    Input Arguments

    expand all

    l — type of transformation. Scalar.

    Scalar that specifies the type of transformation.

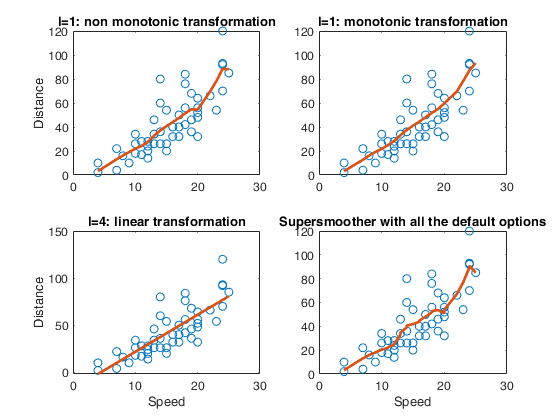
    l=1 => transformation can also be non monotone. In this case, the supersmoother is initially applied. In presence of equal values of x, the unweighted arithmetic mean of the smoothed values is returned.

    l=2 => j-th variable assumes circular (periodic) values in the range (0.0,1.0) with period 1.0.

    l=3 => transformation is to be monotone. In this case, the supersmoother is initially applied. Monotonic transformation is forced applying isotonic regression to (1) the output of the supersmoother and to the flipped upside down (2) output of the supersmoother. The choice between solution (1) and (2) is made based on the output that is closest to the output of the supersmoother.

    Closeness is measured in terms of sum of squares of residuals. Equal consecutive values smoothed values are replaced by linearly interpolated values.

    In presence of equal values of x, the unweighted arithmetic mean of the final smoothed values is returned.

    l=4 => transformation is to be linear. In this case, the smoothed values are simply the fitted values from least squares fit.

    l=5 => the predictor variable is categorical. In this case, the smoothed values are simply the (weighted) values of y in correspondence of each value of x.

    Data Types: single| double

    x — Predictor variable sorted. Vector.

    Ordered abscissa values.

    Note that the x values are assumed non decreasing.

    Data Types: single| double

    y — Response variable. Vector.

    Response variable that has to be smoothed, specified as a vector of length n, where n is the number of observations.

    Data Types: single| double

    Optional Arguments

    w — weights for the observations. Vector.

    Row or column vector of length n containing the weights associated to each observations. If w is not specified, we assume: $w=1$ for $i=1, 2, \ldots, n$.

    Example: 'w',1:n

    Data Types: double

    Output Arguments

    expand all

    ysmo —smoothed values. Vector

    A vector with the same dimension of y containing smoothed values, that is the y values on the fitted curve. The smoothed values come from linear regression, if input value l=4. The smoothed values are monotonic, if input value l=3. The smoothed values can also be non monotonic, if input value l=1;

    References

    Breiman, L. and Friedman, J.H. (1985), Estimating optimal transformations for multiple regression and correlation, "Journal of the American Statistical Association", Vol. 80, pp. 580-597.

    Wang D. and Murphy M. (2005), Identifying nonlinear relationships regression using the ACE algorithm, "Journal of Applied Statistics", Vol. 32, pp. 243-258.

    Friedman, J.H. (1984), A variable span scatterplot smoother. Laboratory for Computational Statistics, Stanford University, Technical Report No. 5.

    See Also

    | | |

    This page has been automatically generated by our routine publishFS