carbikeplotGPCM
carbikeplotGPCM produces the carbike plot to find best relevant clustering solutions
Description
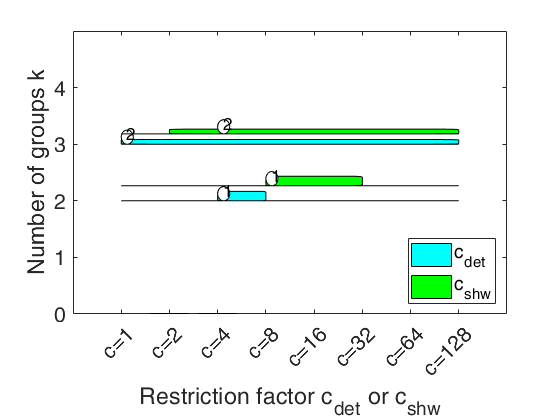
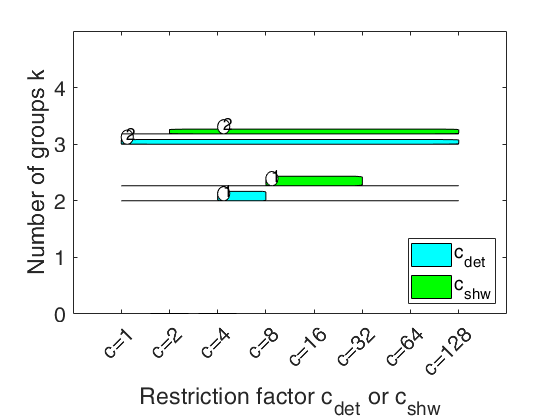
carbikeplotGPCM takes as input the output of function tclustICsolGPCM (that is a structure containing the best relevant solutions) and produces the car-bike plot. This plot provides a concise summary of the best relevant solutions. This plot shows on the horizontal axis the value of $c_{det}$ and $c_{shw}$ restriction factors and on the vertical axis the value of $k$. For each solution we draw two rectangle (associated with $c_{det}$ and $c_{shw}$) which are respectively referred to interval of values for which the solution is best and stable and a horizontal line which departs from the rectangle for the values of $c_{det}$ ($c_{shw}$) in which the solution is only stable.
Finally, for the best value of $c_{det}$ ($c_{shw}$) associated to the solution, we show a circle with a number indicating the ranked solution among those which are not spurious. This plot has been baptized ``car-bike'', because the first best solutions (in general 2 or 3) are generally best and stable for a large number of values of $c$ and therefore will have large rectangles. In addition, these solutions are likely to be stable for additional values of $c_det$ ($c_{shw}$) and therefore are likely to have horizontal lines departing from the rectangles (from here the name ``cars''). Finally, local minor solutions (which are associated with particular values of $c_{det}$ ($c_{shw}$) and $k$) do not generally present rectangles or lines and are shown with circles (from here the name ``bikes'')
car-bike plot for the geyser data.h
=carbikeplotGPCM(RelSol,
Name, Value)
Examples
Simulated data with 3 components.
Simulated data with 3 components.Data generation rng('default') Reinitialize the random number generator to its startup configuration
rng(10); ktrue=3; % n = number of observations n=150; % v= number of dimensions v=2; % Imposed average overlap and restriction factor. BarOmega=0.04; restrfact=5; outMS=MixSim(ktrue,v,'BarOmega',BarOmega, 'restrfactor',restrfact); % data generation given centroids and cov matrices [Y,id]=simdataset(n, outMS.Pi, outMS.Mu, outMS.S); % Number of subsets to extract nsamp=100; % Computation of information criterion using MIXMIX outICmixt=tclustICgpcm(Y,'plots',0,'nsamp',nsamp,'kk',1:4); % Specify number of solutions NumberOfBestSolutions=3; % Extract the best solutions using as Information criterion MIXMIX [outMIXMIX]=tclustICsolGPCM(outICmixt,'whichIC','MIXMIX','plots',0,'NumberOfBestSolutions',NumberOfBestSolutions); carbikeplotGPCM(outMIXMIX);
k=1 k=2 k=3 k=4
car-bike plot for the geyser data.
car-bike plot for the geyser data.
Y=load('geyser2.txt');
out=tclustICgpcm(Y,'cleanpool',false,'plots',0,'alpha',0.1,'nsamp',100,'kk',2:4);
% Find the best solutions using as Information criterion MIXMIX
disp('Best solutions using MIXMIX')
[outMIXMIX]=tclustICsolGPCM(out,'whichIC','MIXMIX','plots',0,'NumberOfBestSolutions',3);
% Produce the car-bike plot
carbikeplotGPCM(outMIXMIX)k=2
k=3
k=4
Best solutions using MIXMIX
ans =
Figure (2) with properties:
Number: 2
Name: ''
Color: [0.9400 0.9400 0.9400]
Position: [488 242 560 420]
Units: 'pixels'
Use GET to show all properties
Input Arguments
Output Arguments
References
Cerioli, A. Garcia-Escudero, L.A., Mayo-Iscar, A. and Riani, M. (2017), Finding the Number of Groups in Model-Based Clustering via Constrained Likelihoods, "Journal of Computational and Graphical Statistics", pp. 404-416, https://doi.org/10.1080/10618600.2017.1390469