mcdeda

mcdeda monitors Minimum Covariance Determinant for a series of values of bdp

expand all in page

Syntax

Description

example

RAW =mcdeda(Y) Example of monitoring of raw and reweighted Mahalanobis distances.

example

RAW =mcdeda(Y, Name, Value) Monitoring reweighted MD using two different confidence levels for reweighting.

example

[RAW, REW] =mcdeda(___) Example with mild contamination.

example

[RAW, REW, varargout] =mcdeda(___) Example with strong contamination.

Examples

expand all

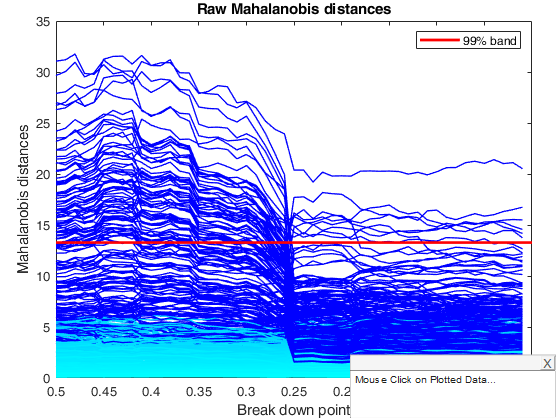
  • Example of monitoring of raw and reweighted Mahalanobis distances.

    • This example enables to obtain Figure 6 of CRAC2018. 

    Y = load('geyser.txt');
% Reweighted MD found using a confidence band for raw Mahalanobis distances
% equal to 0.99
conflev=0.99;
[RAW,REW]=mcdeda(Y,'conflev',conflev,'msg',false);
fground=struct;
fground.funit='';
fground.fthresh=1000;
% Add a horizontal line corresponding to 99 per cent confidence band
conflevplot=0.99;
% Monitoring of raw (squared) Mahalanobis distances
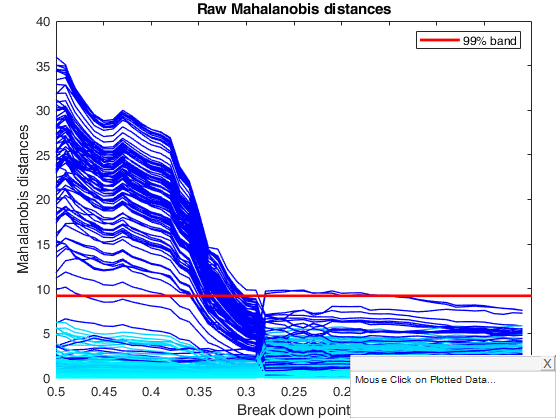
malfwdplot(RAW,'conflev',conflevplot,'fground',fground,'tag','rawMD')
title('Raw Mahalanobis distances')
% Monitoring of reweighted (squared) Mahalanobis distances
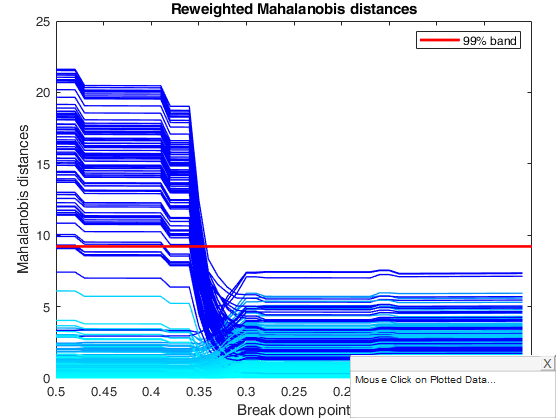
malfwdplot(REW,'conflev',conflevplot,'fground',fground,'tag','rewMD')
title('Reweighted Mahalanobis distances')
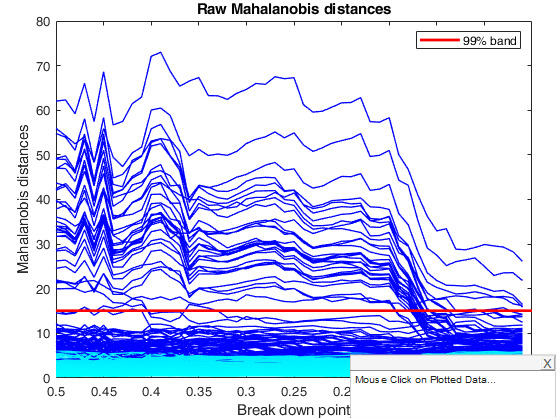
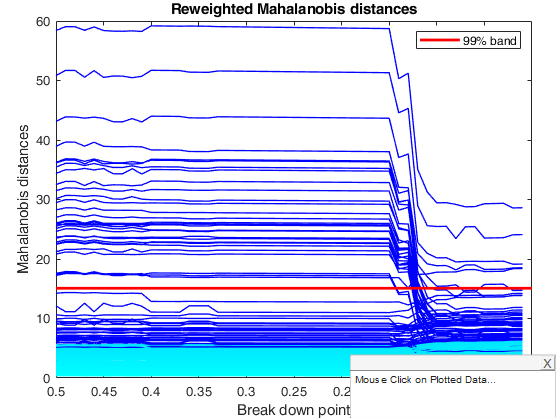
% Comment to the two plots. The squared robust raw distances initially decrease
% steadily. Then, at a bdp around 0.29 there is an abrupt change to a fit
% displaying two or three large distances which remains sensibly constant
% until the MLE is reached at bdp = 0.
% The plot for reweighted square Mahalanobis distances is much more stable
% than that for the crude MCD until 0.37, at which bdp there is a collapse
% to the MLE. The right-hand parts of both panels are similar. However, the
% distances for the crude MCD decreasing as successive observations are
% added to the subset used in fitting. On the other hand, the reweighted
% MCD shows three regions during which the distances are constant. In these
% regions the effect of changing the bdp in the (raw) first stage does not
% cause any change in the units chosen by the reweighting procedure
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Monitoring reweighted MD using two different confidence levels for reweighting.

    • This example enables to obtain Figure 7 of CRAC2018. 

    Y = load('geyser.txt');
% Reweighted MD found using a confidence band for raw Mahalanobis distances
% equal to 0.99
conflev=0.95;
[~,outrew095]=mcdeda(Y,'conflev',conflev,'msg',false);
fground=struct;
fground.funit='';
fground.fthresh=1000;
% Add a horizontal line corresponding to 99 per cent confidence band
conflevplot=0.99;
% Monitoring of raw (squared) Mahalanobis distances
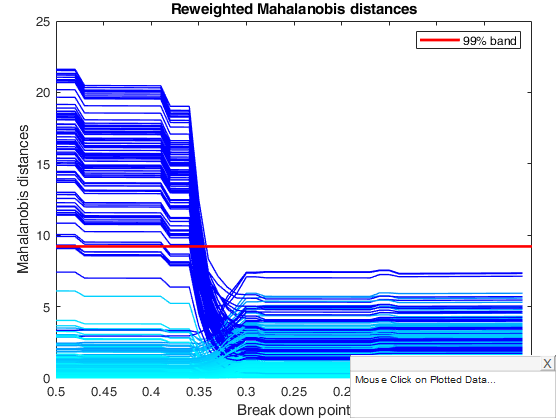
malfwdplot(outrew095,'conflev',conflevplot,'fground',fground,'tag','rewMDclev095')
title('Reweighted Mahalanobis distances using conflev=0.95 for reweighting')
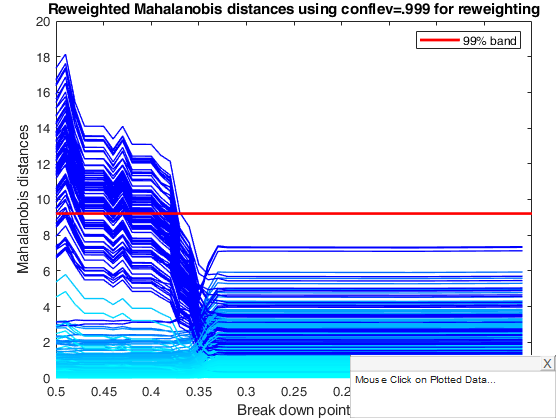
conflev=0.999;
[~,outrew0999]=mcdeda(Y,'conflev',conflev,'msg',false);
% Monitoring of reweighted (squared) Mahalanobis distances
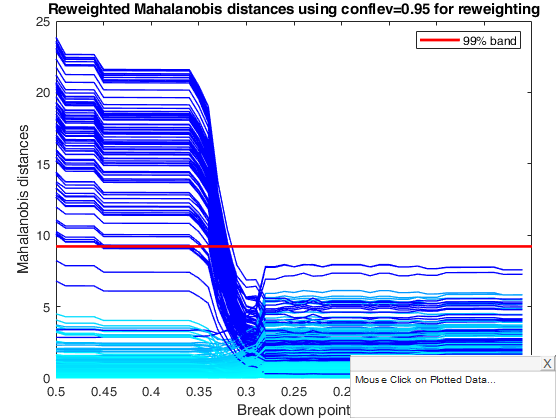
malfwdplot(outrew0999,'conflev',conflevplot,'fground',fground,'tag','rewMDclev0999')
title('Reweighted Mahalanobis distances using conflev=.999 for reweighting')
% The monitoring approach also helps to appreciate the effect of the
% threshold used in the reweighting step. Although the message conveyed by
% the two plots is broadly the same, the less efficient 95 per cent
% threshold produces a few more outliers and a neater separation between
% the two populations, while increasing efficiency in the reweighting step
% causes the inclusion of some contaminated units at a slightly larger bdp
% than 0.37
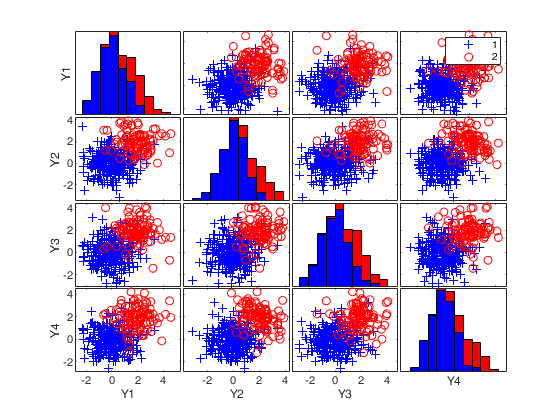
    Click here for the graphical output of this example (link to Ro.S.A. website).

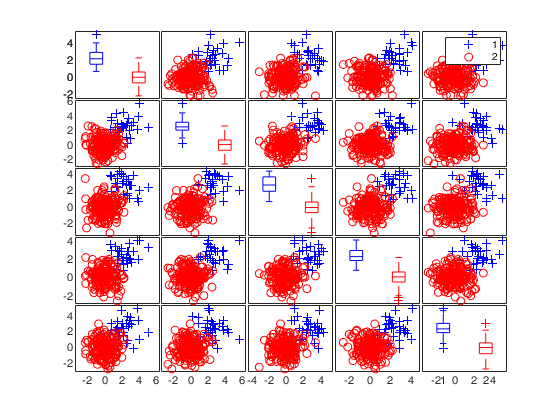
  • Example with mild contamination.

    • This example enables to obtain left panel of Figure 15 of CRAC2018. 

    % In this simulated example there are 200 five-dimensional
% observations, all simulated with standard normal co-ordinates. Thirty of
% the observations had a displacement of 2.4 added to each co-ordinate. As
% a result the outliers are grouped, with virtually no overlap with the
% central 170 observations.
rng('default')
rng(100)
n=200;
v=5;
Xsel=randn(n,v);
kk=2.4;
numcont=30;
Xsel(1:numcont,:)=Xsel(1:numcont,:)+kk;
group=ones(n,1);
group(numcont+1:n)=2;
spmplot(Xsel,group,[],'box');
Y=Xsel;
conflev=0.99;
[outraw,outrew]=mcdeda(Y,'conflev',conflev,'msg',false);
fground=struct;
fground.funit='';
fground.fthresh=1000;
% Add a horizontal line corresponding to 99 per cent confidence band
conflevplot=0.99;
% Monitoring of raw (squared) Mahalanobis distances
malfwdplot(outraw,'conflev',conflevplot,'fground',fground,'tag','rawMD')
title('Raw Mahalanobis distances')
% Monitoring of reweighted (squared) Mahalanobis distances
malfwdplot(outrew,'conflev',conflevplot,'fground',fground,'tag','rewMD')
title('Reweighted Mahalanobis distances')
% The plot for the MCD is very jagged but does show the change in the
% pattern of distances around a bdp of 0.14. The monitoring plot for the
% reweighted MCD with a pointwise threshold of 0.99 is much the same as
% that for the original MCD, including a dramatic change at a bdp of 0.14
% The conclusion of this example is that most of the methods work well with
% a light amount of contamination well separated from the main body of the
% data. In general monitoring allows us to choose values of efficiency or
% breakdown point that give estimators that are as efficient as possible:
% that is, they exclude the outliers while fitting the “good”
% observations.
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Example with strong contamination.

    • This example enables to obtain Figure 20 of CRAC2018. 

    % In this example there are 400 four-dimensional standard normal random
% variables, one hundred of them being displaced by an amount 2 in each
% dimension. There is thus some overlap between the 25 per cent of outliers
% and the uncontaminated data.
rng('default')
rng(100)
n=400;
v=4;
Xsel=randn(n,v);
kk=2;
Xsel(301:400,:)=Xsel(301:400,:)+kk;
group=ones(n,1);
group(301:400)=2;
spmplot(Xsel,group);
Y=Xsel;
conflev=0.99;
[outraw,outrew]=mcdeda(Y,'conflev',conflev,'msg',false);
fground=struct;
fground.funit='';
fground.fthresh=1000;
% Add a horizontal line corresponding to 99 per cent confidence band
conflevplot=0.99;
% Monitoring of raw (squared) Mahalanobis distances
malfwdplot(outraw,'conflev',conflevplot,'fground',fground,'tag','rawMD')
title('Raw Mahalanobis distances')
% Monitoring of reweighted (squared) Mahalanobis distances
malfwdplot(outrew,'conflev',conflevplot,'fground',fground,'tag','rewMD')
title('Reweighted Mahalanobis distances')
% Comment to the plots: when bdp is 50%, 64 outliers are found using
% $\Chi^2_{4,0.99}$ (60 belong to the group of contaminated units). These
% are shown in the plot of raw Mahalanobis distances. Reweighting the
% output of this analysis leads to the detection of only 9 outliers (7
% belong to the group of contaminated units) as is shown in the plot of the
% reweighted distances. This plot shows how the distribution of distances
% for the 100 contaminated units is changed by the parameter estimates from
% reweighting. However, the distribution of these distances is even so
% quite distinct from those from the uncontaminated units. This effect of
% reweighting, which is not substantially affected by the choice of the
% reweighting threshold, is quite different from that shown in the case of
% lightly contaminated data, where weighted and unweighted analyses were
% comparable. However, monitoring the MCD is still very informative. The
% plot of raw distances shows a striking change around a bdp of 0.27 as the
% outliers start to be included in the central part of the data. In the
% monitoring plot for the reweighted MCD there is a change around a bdp of
% 0.28 when some Mahalanobis distances slightly increase in magnitude. For
% lower values of the bdp the plots in the two panels are similar; just 9
% observations are identified as outlying.
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Input Arguments

    expand all

    Y — Data matrix containing n observations on v variables. Rows of Y represent observations, and columns represent variables.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will be excluded from the computations.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'bdp',[0.5 0.4 0.3 0.2 0.1] , 'bestr',10 , 'betathresh',false , 'conflev',0.99 , 'msg',false , 'nocheck',true , 'nsamp',10000 , 'refsteps',10 , 'refstepsbestr',10 , 'reftol',1e-8 , 'reftolbestr',1e-8 , 'smallsamplecor',true , 'tolMCD',1e-20 , 'plots',1

    bdp —breakdown point.scalar | vector.

    It measures the fraction of outliers the algorithm should resist. In this case any value greater than 0 but smaller or equal than 0.5 will do fine.

    The default value of bdp is a sequence from 0.5 to 0.01 with step 0.01

    Example: 'bdp',[0.5 0.4 0.3 0.2 0.1]

    Data Types: double

    bestr —Number of best solutions to store.scalar.

    Number of "best locations" to remember from the subsamples. These will be later iterated until convergence (default=5)

    Example: 'bestr',10

    Data Types: double

    betathresh —Distribution to use.boolean.

    If betathresh = true the distribution which is used to declare units as outliers is a mixture of Rocke scaled F distribution and Beta else (default) traditional chi^2 distribution is used.

    Example: 'betathresh',false

    Data Types: logical

    conflev —Confidence level.scalar.

    Number between 0 and 1 containing confidence level which is used to declare units as outliers and to perform reweighting.

    Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).

    Default value is 0.975

    Example: 'conflev',0.99

    Data Types: double

    msg —Display or not messages on the screen.boolean.

    If msg==true (default) messages are displayed on the screen about estimated time to compute the final estimator for each value of bdp else no message is displayed on the screen.

    Example: 'msg',false

    Data Types: logical

    nocheck —No check on input data.boolean.

    If nocheck is equal to true no check is performed on matrix Y. As default nocheck=false.

    Example: 'nocheck',true

    Data Types: logical

    nsamp —Number of subsamples.scalar | matrix.

    If nsamp is a scalar, it contains the number of subsamples of size v+1 which have to be extracted (if not given, default is nsamp=1000). If nsamp=0 all subsets will be extracted. If nsamp is a matrix it contains in the rows the indexes of the subsets which have to be extracted. nsamp in this case can be conveniently generated by function subsets.

    Example: 'nsamp',10000

    Data Types: double

    refsteps —Number of refining iterations.scalar.

    Number of refining iterations in each subsample (default = 3).

    refsteps = 0 means "raw-subsampling" without iterations.

    Example: 'refsteps',10

    Data Types: double

    refstepsbestr —Number of refining iterations.scalar.

    Number of refining iterations for each best subset (default = 50).

    Example: 'refstepsbestr',10

    Data Types: double

    reftol —Refining steps tolerance.scalar.

    Tolerance for the refining steps.

    The default value is 1e-6;

    Example: 'reftol',1e-8

    Data Types: double

    reftolbestr —Tolerance for refining steps.scalar.

    Value of tolerance for the refining steps for each of the best subsets.

    The default value is 1e-8;

    Example: 'reftolbestr',1e-8

    Data Types: double

    smallsamplecor —small sample correction factor.boolean.

    Boolean which defines whether to use or not small sample correction factor to inflate the scale estimate. If it is equal to true the small sample correction factor is used.

    The default value of smallsamplecor is true, that is the correction is used.

    Example: 'smallsamplecor',true

    Data Types: logical

    tolMCD —Tolerance to declare a subset as singular.scalar.

    The default value of tolMCD is exp(-50*v).

    Example: 'tolMCD',1e-20

    Data Types: double

    plots —Plot on the screen.scalar.

    If plots is a scalar equal to 1, it generates two plots of Mahalanobis distances monitoring (raw and reweighted) against values of bdp.

    The confidence level used to draw the confidence bands for the MD is given by the input option conflev. If conflev is not specified a nominal 0.975 confidence interval will be used.

    Example: 'plots',1

    Data Types: double

    Output Arguments

    expand all

    RAW — description Structure

    Structure which contains the following fields

    Value Description
    bdp

    values of bdp which have been used.
    conflev

    Confidence level that was used to declare outliers and to perform reweighting.
    Cov

    array of size v-by-v-length(bdp) containing robust MCD estimate of covariance matrix. It is the raw MCD covariance matrix (multiplied by a finite sample correction factor and an asymptotic consistency factor).
    h

    length(bdp)-times-1 vector. It contains for each value of bdp the number of observations that have determined the raw MCD estimator
    obj

    length(bdp)-times-1 vector. The determinant of the raw MCD covariance matrix.
    Loc

    length(bdp)-times-v matrix containing raw MCD location of the data for each value of bdp
    MAL

    n-times-length(bdp) matrix containing the estimates of the robust Mahalanobis distances (in squared units). This matrix contains the distances of each observation from the raw MCD location of the data, relative to the raw MCD scatter matrix RAW.cov
    Outliers

    A boolean matrix of size n-by-length(bdp) containing the list of the units declared as outliers by raw MCD using confidence level specified in input scalar conflev.
    Weights

    n x length(bdp) boolean matrix containing the estimates of the weights. Weights assume values 0 (false) or 1 (true). Weight is 1 (true) if the associated observation has been used to compute centroid and covariance matrix. These weights determine which observations are used to compute the final MCD estimates. Unless there is a perfect fit sum(RAW.weights,1)=RAW.h'
    Y

    Data matrix Y.
    class

    'mcdeda'

    REW — description Structure

    Structure which contains the following fields:

    Value Description
    bdp

    values of bdp which have been used.
    Cov

    array of size v-by-v-length(bdp) containing robust covariance matrix, obtained after reweighting and multiplying by a finite sample correction factor and an asymptotic consistency factor, if the raw MCD is not singular. Otherwise the raw MCD covariance matrix is given here.
    Loc

    length(bdp)-times-v matrix containing robust location estimate of the data, obtained after reweighting for each value of bdp.
    MAL

    n-times-length(bdp) matrix containing the estimates of the robust Mahalanobis distances (in squared units) each observation from the reweighted MCD location of the data, relative to the reweighted MCD scatter of the data If the reweighted MCD is singular, raw distance is given here.
    Outliers

    A boolean matrix of size n-by-length(bdp) containing the list of the units declared as outliers by reweighted MCD using confidence level specified in input scalar conflev.
    Weights

    n x 1 vector containing the estimates of the weights.

    Weights assume values 0 or 1. Weight is 0 if the associated observation has been declared outlier.

    These weights determine which observations are used to compute the final MCD estimates.

    Remark: if the reweighted MCD is singular, RAW.weights is given here.
    Y

    Data matrix Y.
    class

    'mcdeda'.

    varargout —Indices of the subsamples extracted for computing the estimate. C : matrix of size nsamp-by-v

    More About

    expand all

    Additional Details

    MCD computes the MCD estimator of a multivariate data set. This estimator is given by the subset of h observations with smallest covariance determinant. The MCD location estimate is then the mean of those h points, and the MCD scatter estimate is their covariance matrix.

    Larger values of $h$ give more efficient estimates of the parameters but with lower breakdown point. In this routine we use monitoring to provide an adaptive estimate of the highest value of $h$ which provides a robust fit.

    Finally, we also include in this routine monitoring of the more efficient reweighted MCD estimate that is computed on a second subset of $h^* > h$ observations for which the squared robust distances computed from the raw MCD estimate are below a fixed threshold, often taken from the $\chi^2_v$ distribution or the Beta distribution (depending on input option $betathresh$).

    References

    Rousseeuw, P.J. (1984), Least Median of Squares Regression, "Journal of the American Statistical Association", Vol. 79, pp. 871-881.

    Rousseeuw, P.J. and Van Driessen, K. (1999). A fast algorithm for the minimum covariance determinant estimator. Technometrics, 41:212-223.

    Maronna, R.A., Martin D. and Yohai V.J. (2006), "Robust Statistics, Theory and Methods", Wiley, New York.

    Cerioli A., Riani M., Atkinson A.C., Corbellini A. (2018). "The power of monitoring: how to make the most of a contaminated multivariate sample, "Statistical Methods and Applications (with discussion)", Vol. 27, pp. 559–587. [CRAC2018]

    See Also

    |

    This page has been automatically generated by our routine publishFS