tBothSides

tBothSides allows users to transform both sides of a (nonlinear) regression model.

expand all in page

Syntax

out=tBothSides(y, X)example
out=tBothSides(y, X,Name,Value)example

Description

example

out =tBothSides(y, X) Call of tBothSides with all default options.

example

out =tBothSides(y, X, Name, Value) Call of tBothSides with parameter lambda fixed.

Examples

expand all

Call of tBothSides with all default options.

Load Assay data from Davidian M. and Haaland P. (1989).

% The Relationship Between Transformation and Weighting
% in Regression, With Application to Biological and Physical Science,
% Institute of Statistics mimeo series Report 1947, North Carolina State University. 
% File is downloadable from
% https://pdfs.semanticscholar.org/7067/fd66fe06f114cac58eef8253eb7483edfd29.pdf
% The material assayed was obtained from two sources, with every other
% concentration starting with 0.476 from the first source and the remainder from the
% second. Replicate observations were obtained by subsampling at each concentration.
x=[0.476	0.924	1.905	3.696	7.619	14.874	30.474	59.134];
yy=[0.05706	0.11781	0.25071	0.49596	1.03928	2.14635	4.24397	8.53848...
0.057	0.11615	0.25398	0.4807	1.03659	2.09495		    8.41333...
0.06363	0.12587	0.24552	0.49442	1.12641	2.24941	4.7011	9.01437...
0.05566	0.12308	0.24889	0.52321	1.10456	2.19937	4.44709	8.73544...
0.05449	0.11629	0.24858	0.49931	1.03184	2.16042	4.42707	8.33862...
0.06153	0.11878	0.24657	0.5021	1.02598	2.09198	4.39725	8.33347...
0.05837	0.11869	0.24212	0.4886	0.98267	2.07686	4.35511	8.35725...
0.05388	0.11886	0.25975	0.48158	1.04321	2.06961	4.37357	8.39123...
0.05618	0.12492	0.25311	0.4827	1.03838	2.12548	4.3204	8.3901];
X=[x';x([1:6 8])'; repmat(x(:),7,1)];
y=yy';
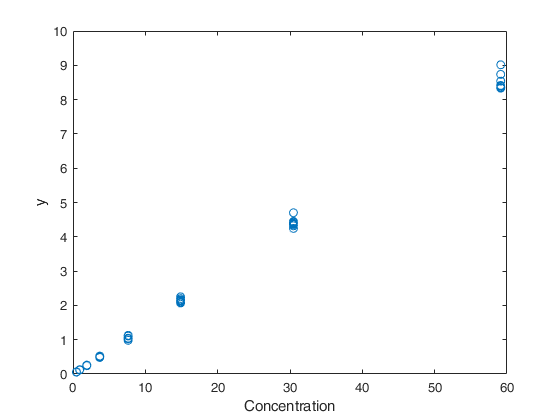
% The plot of the data shows: a systematic increase in variance with level
% of mean response, small variability relative to the range of the means,
% and reasonably straight-line relationship.
plot(X,y,'o')
xlabel('Concentration')
ylabel('y')
% In this case both lambda and the beta coefficients are estimated
% A linear link between X and beta is assumed
out=tBothSides(y, X);
disp(out.Btable)

                bhat           se         tstat 
              _________    __________    _______

    b1        -0.010677     0.0010009    -10.667
    b2          0.14143    0.00085986     164.47
    lambda     0.063929      0.081648    0.78298

Click here for the graphical output of this example (link to Ro.S.A. website).

Call of tBothSides with parameter lambda fixed.

x=[0.476	0.924	1.905	3.696	7.619	14.874	30.474	59.134];
yy=[0.05706	0.11781	0.25071	0.49596	1.03928	2.14635	4.24397	8.53848...
0.057	0.11615	0.25398	0.4807	1.03659	2.09495		    8.41333...
0.06363	0.12587	0.24552	0.49442	1.12641	2.24941	4.7011	9.01437...
0.05566	0.12308	0.24889	0.52321	1.10456	2.19937	4.44709	8.73544...
0.05449	0.11629	0.24858	0.49931	1.03184	2.16042	4.42707	8.33862...
0.06153	0.11878	0.24657	0.5021	1.02598	2.09198	4.39725	8.33347...
0.05837	0.11869	0.24212	0.4886	0.98267	2.07686	4.35511	8.35725...
0.05388	0.11886	0.25975	0.48158	1.04321	2.06961	4.37357	8.39123...
0.05618	0.12492	0.25311	0.4827	1.03838	2.12548	4.3204	8.3901];
X=[x';x([1:6 8])'; repmat(x(:),7,1)];
y=yy';
% In this case only the beta coefficients are estimated
la=0.063;
% A linear link between X and beta is assumed
out=tBothSides(y, X,'la',la);

Related Examples

expand all

Example of tBothSides with non linear link between X and beta.

Load spawners data (table 4.1 p. 141 Book CR) year spawner (S) recruiter (R) Model is R = \beta_1 S exp ( - \beta_2 S) = f_RK(S, \beta)

XX=[1940 963 2215
1941 572 1334
1942 305 800
1943 272 438
1944 824 3071
1945 940 957
1946 486 934
1947 307 971
1948 1066 2257
1949 480 1451
1950 393 686
1951 176 127
1952 237 700
1953 700 1381
1954 511 1393
1955 87 363
1956 370 668
1957 448 2067
1958 819 644
1959 799 1747
1960 273 744
1961 936 1087
1962 558 1335
1963 597 1981
1964 848 627
1965 619 1099
1966 397 1532
1967 616 2086];
% Row 12 is removed from the analysis.
XX(12,:)=[];
X=XX(:,2);
y=XX(:,3);
% Call of tBothSides non linear link between X and beta.
% In this case modelfun (function which specifies the link between X and beta) and
% the vector of initial regression coefficients is specified.
% This is the spawner recruiter model. See CR for more details.
modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
% Initial value of beta coefficients
bini=[3; 0.0009];
% The link between X and beta is specified inside modelfun given at the end
% of the example
out=tBothSides(y, X,'modelfun',modelfun,'beta0',bini,'family','BoxCox','dispresults',true);
% Plot the original values together with estimated median regression lines
% and 90 per cent confidence interval for fitted response.
close all
plot(X,y,'o')
hold('on')
laest=out.betaout(end);
upConfInt= normBoxCox(out.yhattra+1.65*out.scale,1,laest,'inverse',true,'Jacobian',false);
lowConfInt= normBoxCox(out.yhattra-1.65*out.scale,1,laest,'inverse',true,'Jacobian',false);
[Xsor,indXsor]=sort(X);
% Plot the estimated median recruitment
plot(Xsor,out.yhat(indXsor),'r-')
% Plot the estimated 95th percentile of recruitment
plot(Xsor,upConfInt(indXsor),'r--')
% Plot the estimated 5th percentile of recruitment
plot(Xsor,lowConfInt(indXsor),'r--')
ylabel('Recruiters')
xlabel('Spawners')

Example where only beta coefficents are estimated and initial values for beta are provided.

x=[0.476	0.924	1.905	3.696	7.619	14.874	30.474	59.134];
yy=[0.05706	0.11781	0.25071	0.49596	1.03928	2.14635	4.24397	8.53848...
0.057	0.11615	0.25398	0.4807	1.03659	2.09495		    8.41333...
0.06363	0.12587	0.24552	0.49442	1.12641	2.24941	4.7011	9.01437...
0.05566	0.12308	0.24889	0.52321	1.10456	2.19937	4.44709	8.73544...
0.05449	0.11629	0.24858	0.49931	1.03184	2.16042	4.42707	8.33862...
0.06153	0.11878	0.24657	0.5021	1.02598	2.09198	4.39725	8.33347...
0.05837	0.11869	0.24212	0.4886	0.98267	2.07686	4.35511	8.35725...
0.05388	0.11886	0.25975	0.48158	1.04321	2.06961	4.37357	8.39123...
0.05618	0.12492	0.25311	0.4827	1.03838	2.12548	4.3204	8.3901];
X=[x';x([1:6 8])'; repmat(x(:),7,1)];
y=yy';
% Initial value of beta coefficients
bini=[3; 0.0009];
% lambda is fixed
la=-0.2;
% modelfun is the function which specifies the link between X and beta
% This is the spawner recruiter model. See CR for more details.
modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
out=tBothSides(y, X,'modelfun',modelfun,'beta0',bini,'la',la);

Example of the use of option dispresults.

modelfun is the function which specifies the link between X and beta This is the spawner recruiter model. See CR for more details.

x=[0.476	0.924	1.905	3.696	7.619	14.874	30.474	59.134];
yy=[0.05706	0.11781	0.25071	0.49596	1.03928	2.14635	4.24397	8.53848...
0.057	0.11615	0.25398	0.4807	1.03659	2.09495		    8.41333...
0.06363	0.12587	0.24552	0.49442	1.12641	2.24941	4.7011	9.01437...
0.05566	0.12308	0.24889	0.52321	1.10456	2.19937	4.44709	8.73544...
0.05449	0.11629	0.24858	0.49931	1.03184	2.16042	4.42707	8.33862...
0.06153	0.11878	0.24657	0.5021	1.02598	2.09198	4.39725	8.33347...
0.05837	0.11869	0.24212	0.4886	0.98267	2.07686	4.35511	8.35725...
0.05388	0.11886	0.25975	0.48158	1.04321	2.06961	4.37357	8.39123...
0.05618	0.12492	0.25311	0.4827	1.03838	2.12548	4.3204	8.3901];
X=[x';x([1:6 8])'; repmat(x(:),7,1)];
y=yy';
% Initial value of beta coefficients
bini=[3; 0.0009];
modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
out=tBothSides(y, X,'modelfun',modelfun,'dispresults',true,'beta0',bini);
% modelfun is the function which specifies the link between X and beta
%     % This is the spawner recruiter model
%     function [yhat]=modelfun(beta, X)
%     yhat=X*beta(1).*exp(-beta(2)*X);
%     end

Example of the use of option prolik.

This is the spawner recruiter model. See CR for more details.

% modelfun is the function which specifies the link between X and beta
x=[0.476	0.924	1.905	3.696	7.619	14.874	30.474	59.134];
yy=[0.05706	0.11781	0.25071	0.49596	1.03928	2.14635	4.24397	8.53848...
0.057	0.11615	0.25398	0.4807	1.03659	2.09495		    8.41333...
0.06363	0.12587	0.24552	0.49442	1.12641	2.24941	4.7011	9.01437...
0.05566	0.12308	0.24889	0.52321	1.10456	2.19937	4.44709	8.73544...
0.05449	0.11629	0.24858	0.49931	1.03184	2.16042	4.42707	8.33862...
0.06153	0.11878	0.24657	0.5021	1.02598	2.09198	4.39725	8.33347...
0.05837	0.11869	0.24212	0.4886	0.98267	2.07686	4.35511	8.35725...
0.05388	0.11886	0.25975	0.48158	1.04321	2.06961	4.37357	8.39123...
0.05618	0.12492	0.25311	0.4827	1.03838	2.12548	4.3204	8.3901];
X=[x';x([1:6 8])'; repmat(x(:),7,1)];
y=yy';
% Initial value of beta coefficients
bini=[3; 0.0009];
modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
out=tBothSides(y, X,'modelfun',modelfun,'prolik',true,'beta0',bini);

Input Arguments

expand all

`y` — Response variable. Vector.

Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.

Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

Data Types: single| double

`X` — Predictor variables. Matrix.

Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.

Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

Data Types: single| double

Name-Value Pair Arguments

Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

Example:

 'la',0.5
, 'modelfun', modelfun where modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
, 'beta0',[0.5 0.2 0.1]
, 'la',1
, 'intercept',true
, 'family','YJ'
,'prolik',true
, 'dispresults',false

`la` —transformation parameter.scalar | empty value (default).

Transformation parameter to estimate or prefixed value of lambda to apply to both sides of the equation. If la is empty (default), lambda will be estimated by the non linear least squares routine. If la is given, the supplied value will be used transform both sides of the equation and only beta parameters will be used.

Example: 'la',0.5

Data Types: double

`modelfun` —non linear function to use.function_handle | empty value (default).

If modelfun is empty the link between X and \beta is assumed to be linear else it is necessary to specify a function (using @) that accepts two arguments, a coefficient vector and the array X and returns the vector of fitted values from the non linear model y. For example, to specify the hougen (Hougen-Watson) nonlinear regression function, use the function handle @hougen.

Example: 'modelfun', modelfun where modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);

Data Types: function_handle or empty value

`beta0` —empty value or vector containing initial values for the coefficients just in case modelfun is non empty.if modelfun is empty this argument is ignored.

Example: 'beta0',[0.5 0.2 0.1]

Data Types: double

`la0` —initial value for transformation parameter.scalar | empty value.

If optional input parameter la is empty, it is possible to specify the initial value to use in the non linear least squares routine. This argument is ignored if la is nont empty.

Example: 'la',1

Data Types: double

`intercept` —Indicator for constant term.true (default) | false.

If true, and modelfun is empty (that is if the link between X and beta is linear) a model with constant term will be fitted (default), else no constant term will be included.

This argument is ignored if modelfun is not empty.

Example: 'intercept',true

Data Types: boolean

`family` —parametric transformation to use.string.

String which identifies the family of transformations which must be used. Character. Possible values are 'BoxCox' (default) or 'YJ'.

The Box-Cox family of power transformations equals $(y^{\lambda}-1)/\lambda$ for $\lambda$ not equal to zero, and $\log(y)$ if $\lambda = 0$.

The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of $y+1$ for nonnegative values, and of $|y|+1$ with parameter 2-lambda for y negative.

The basic power transformation returns $y^{\lambda}$ if $\lambda$ is not zero, and $\log(\lambda)$ otherwise.

Remark. BoxCox and the basic power family can be used just if input y is positive. Yeo-Johnson family of transformations does not have this limitation.

Example: 'family','YJ'

Data Types: char

`prolik` —Monitor profile log likelihood for lambda.empty value (default), scalar | structure.

It specifies whether it is necessary to show the profile log likelihood of lambda If prolik is a Boolean and is equal to true, the plot of the profile loglikelihood is produced together with a 95 per cent confidence interval. The default value of prolik is false, that is no plot is produced.

If prolik is a structure it may contain the following fields:

Value Description

Value	Description
`conflev`	scalar between 0 and 1 determining confidence level for lambda based on the asymptotic chi1^2 of twice the loglikelihood ratio. The default confidence level is 0.95;
`xlim`	vector with two elements determining minimum and maximum values of lambda in the plots of profile loglikelihoods. The default value of xlim is [-2 2];
`LineWidth`	line width of the vertical lines defining confidence levels of the transformation parameters.

conflev

scalar between 0 and 1 determining confidence level for lambda based on the asymptotic chi1^2 of twice the loglikelihood ratio.

The default confidence level is 0.95;

xlim

vector with two elements determining minimum and maximum values of lambda in the plots of profile loglikelihoods. The default value of xlim is [-2 2];

LineWidth

line width of the vertical lines defining confidence levels of the transformation parameters.

Example: 'prolik',true

Data Types: Boolean or struct

`dispresults` —Display results on the screen.boolean.

If dispresults is true (default) it is possible to see on the screen table Btable.

Example: 'dispresults',false

Data Types: Boolean

Output Arguments

expand all

`out` — description Structure

A structure containing the following fields

Value	Description
`betaout`	Column vector containing estimated beta coefficients (including the intercept if requested) and input option la is empty estimate of lambda (in the last element)
`covB`	Matrix containing variance covariance matrix of estimated coefficients
`Btable`	table containing estimated beta coefficients, standard errors, t-stat and p-values The content of matrix B is as follows: 1st col = beta coefficients and lambda (in the last element if input option la is empty). 2nd col = standard errors; 3rd col = t-statistics; 4th col = p values. Remark: note that the pseudo-model technique (see CR p. 126) is used and this method only produces consistent estiates of the standard errors of beta and not of lambda. If the user is interested in an asymptotic consistent confidence interval for lambda it is necessary to use input option prolik.
`scale`	scalar containing the estimate of the scale (sigma). The estimate of the scale is the maximum likelihood estimated corrected for the degrees of freedom. It uses equation (4.18) of CR.
`residuals`	n x 1 vector containing the estimates of the scaled residuals in the transformed scale. That is residuals in the transformed scale divided by the estimate of the scale.
`yhat`	n x 1 vector containing the fitted values in the original scale.
`yhattra`	n x 1 vector containing the fitted values in the transformed scale. Transformation which is used is Box Cox or Yao and Johnson.
`ytra`	n x 1 vector containing the response values in the transformed scale. Transformation which is used is Box Cox or Yao and Johnson.

More About

expand all

Additional Details

There is sometimes a strong, often theoretically derived, relationship between the response and the model $\eta(x,\beta)$, combined with variance heterogeneity. Box-Cox transformation of the response to achieve stability of variance can destroy the relationship between E($Y$) and $\eta(x,\beta)$. For example, the kinetic models of chemistry provide deterministic relationships between concentrations of reactants and products and time and temperature. A well-known simple example is the Michaelis-Menten model for enzyme kinetics in which the response goes from zero to an asymptotic value $V_{\mbox{max}}$. Transforming the response to $y^{\lambda}$ would result in a different range for the transformed response.

Carrol and Ruppert (1988) [Chapter~4] developed a transform both sides model for such problems, motivated by theoretical models for sockeye salmon breeding. The transformation model is \begin{equation} \label{BSmodel} (y^{\lambda} - 1)/\lambda = \{\eta(x,\beta)^{\lambda} - 1\}/\lambda + \epsilon, \end{equation} where the independent errors are normally distributed. As with the Box-Cox transformation, the parameters $\lambda$ and $\beta$ are found by minimizing the residual sum of squares in the regression model which includes the Jacobian of the transformation, again $\dot{y}$.

The theoretical procedure is to minimize the residual sum of squares using $y(\lambda)/\dot{y}^{\lambda -1}$, or equivalently $y(\lambda)/\dot{y}^{\lambda}$, as the response and the similarly transformed value of $\eta$ as the model. Carroll and Ruppert comment that, unless $\lambda$ is fixed, it is not possible to use standard nonlinear regression routines for this minimization as such routings typically do not allow the response to depend upon unknown parameters.

They reformulate the problem in terms of a `pseudo model'. This is what is implemented in this routine.

References

Box, G.E.P. and Cox, D.R. (1964), An analysis of transformations (with Discussion), "Journal of the Royal Statistical Society Series B", Vol. 26, pp. 211-252.

Carroll, R.J. and Ruppert, D. (1988), Transformation and Weighting in Regression, London: Chapman and Hall.

Yeo, I.K and Johnson, R. (2000), A new family of power transformations to improve normality or symmetry, "Biometrika", Vol. 87, pp. 954-959.

Documentation

tBothSides

Syntax

Description

Examples

Call of tBothSides with all default options.

Call of tBothSides with parameter lambda fixed.

Related Examples

Example of tBothSides with non linear link between X and beta.

Example where only beta coefficents are estimated and initial values for beta are provided.

Example of the use of option dispresults.

Example of the use of option prolik.

Input Arguments

`y` — Response variable. Vector.

`X` — Predictor variables. Matrix.

Name-Value Pair Arguments

`la` —transformation parameter.scalar | empty value (default).

`modelfun` —non linear function to use.function_handle | empty value (default).

`beta0` —empty value or vector containing initial values for the coefficients just in case modelfun is non empty.if modelfun is empty this argument is ignored.

`la0` —initial value for transformation parameter.scalar | empty value.

`intercept` —Indicator for constant term.true (default) | false.

`family` —parametric transformation to use.string.

`prolik` —Monitor profile log likelihood for lambda.empty value (default), scalar | structure.

`dispresults` —Display results on the screen.boolean.

Output Arguments

`out` — description Structure

More About

Additional Details

References

See Also

tBothSides

Syntax

Description

Examples

Related Examples

Input Arguments

y — Response variable. Vector.

X — Predictor variables. Matrix.

Name-Value Pair Arguments

la —transformation parameter.scalar | empty value (default).

modelfun —non linear function to use.function_handle | empty value (default).

beta0 —empty value or vector containing initial values for the coefficients just in case modelfun is non empty.if modelfun is empty this argument is ignored.

la0 —initial value for transformation parameter.scalar | empty value.

intercept —Indicator for constant term.true (default) | false.

family —parametric transformation to use.string.

prolik —Monitor profile log likelihood for lambda.empty value (default), scalar | structure.

dispresults —Display results on the screen.boolean.

Output Arguments

out — description Structure

More About

References

See Also

`y` — Response variable. Vector.

`X` — Predictor variables. Matrix.

`la` —transformation parameter.scalar | empty value (default).

`modelfun` —non linear function to use.function_handle | empty value (default).

`beta0` —empty value or vector containing initial values for the coefficients just in case modelfun is non empty.if modelfun is empty this argument is ignored.

`la0` —initial value for transformation parameter.scalar | empty value.

`intercept` —Indicator for constant term.true (default) | false.

`family` —parametric transformation to use.string.

`prolik` —Monitor profile log likelihood for lambda.empty value (default), scalar | structure.

`dispresults` —Display results on the screen.boolean.

`out` — description Structure