twdpdf
twdpdf computes the probability density function of the Tweedie distribution.
Syntax
pdf=twdpdf(x,alpha,theta,delta)example
Description
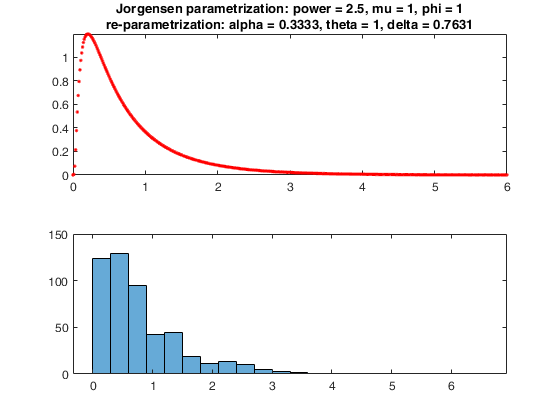
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Tweedie, M. C. K. (1984), An index which distinguishes between some important exponential families, "in Statistics: Applications and New Directions, Proceedings of the Indian Statistical Institute Golden Jubilee International Conference (J.K. Ghosh and J. Roy, eds.), Indian Statistical Institute, Calcutta", pp. 579-604.
 Check consistency with R theedie package.
Check consistency with R theedie package.