CEVmodel
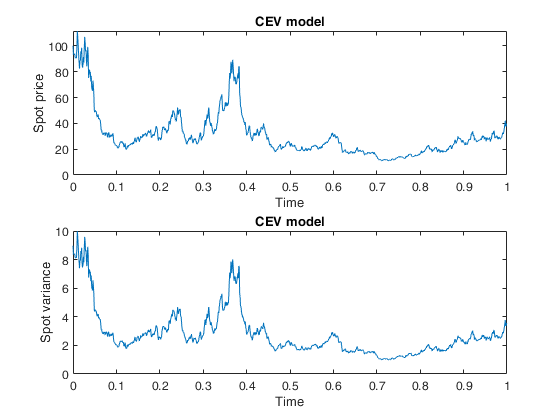
CEVmodel computes price and instantaneous variance processes from the CEV model
Description
CEVmodel computes price and instantaneous variance for the Constant Elasticity of Variance model [S. Beckers, The Journal of Finance, Vol. 35, No. 3, 1980] via Euler method
Examples
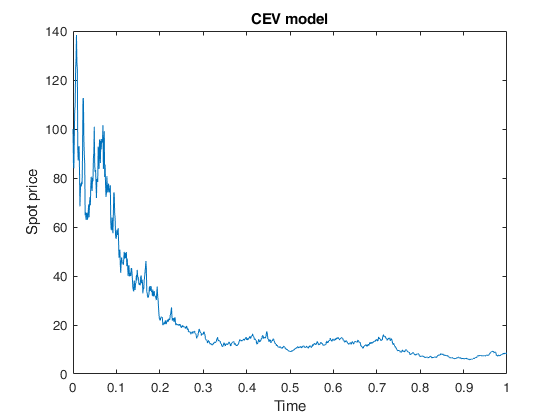
 Example of call of CEVmodel providing only price values.
Example of call of CEVmodel providing only price values.