CorAna
CorAna performs correspondence analysis
Description
Examples
CorAna with all the default options.
load smoke
[N,~,~,labels] =crosstab(smoke{:,1},smoke{:,2});
[I,J]=size(N);
if verLessThan('matlab','8.2.0')==0
% Contingency table is supplied to CorAna in table format
Ntable=array2table(N,'RowNames',labels(1:I,1),'VariableNames',labels(1:J,2))
out=CorAna(Ntable);
else
out=CorAna(N);
end
 CorAna with name pairs.
CorAna with name pairs.
 CorAna with name pairs.
CorAna with name pairs.Input is the contingency table, labels for rows and columns are supplied.
% Data are read from the txt file
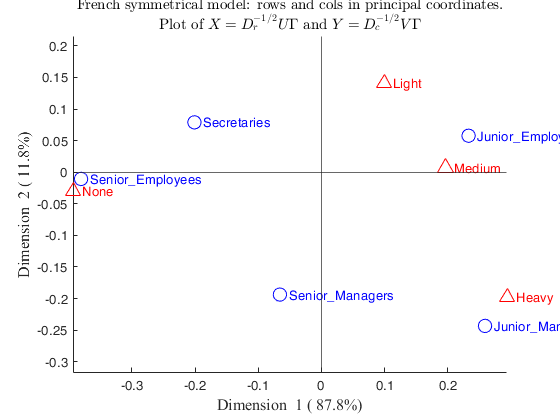
load('smoke.txt')
labels_rows= {'Senior-Managers' 'Junior-Managers' 'Senior-Employees' 'Junior-Employees' 'Secretaries'};
labels_columns= {'None' 'Light' 'Medium' 'Heavy'};
N=crosstab(smoke(:,1),smoke(:,2));
out=CorAna(N,'Lr',labels_rows,'Lc',labels_columns);Summary
Singular_value Inertia Accounted_for Cumulative
______________ __________ _____________ __________
dim_1 0.27342 0.074759 0.87756 0.87756
dim_2 0.10009 0.010017 0.11759 0.99515
dim_3 0.020337 0.00041357 0.0048547 1
ROW POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
Senior_Managers -0.065768 0.0032977 0.092232
Junior_Managers 0.25896 0.083659 0.5264
Senior_Employees -0.38059 0.51201 0.99903
Junior_Employees 0.23295 0.33097 0.94193
Secretaries -0.20109 0.070064 0.86535
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
________ ___________ ___________
Senior_Managers -0.19374 0.21356 0.80034
Junior_Managers -0.2433 0.55115 0.46468
Senior_Employees -0.01066 0.0029976 0.00078372
Junior_Employees 0.057744 0.15177 0.057876
Secretaries 0.078911 0.080522 0.13326
COLUMN POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
________ ___________ ___________
None -0.39331 0.654 0.99402
Light 0.099456 0.03085 0.32673
Medium 0.19632 0.16562 0.98185
Heavy 0.29378 0.14954 0.6844
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
None -0.030492 0.029336 0.0059745
Light 0.14106 0.46317 0.65729
Medium 0.0073591 0.0017368 0.0013796
Heavy -0.19777 0.50575 0.31015
-----------------------------------------------------------
Overview ROW POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
________ _________ ________ _________ _____________ _____________ _____________ _____________
Senior_Managers 0.056995 -0.065768 -0.19374 0.0026729 0.0032977 0.21356 0.092232 0.80034
Junior_Managers 0.093264 0.25896 -0.2433 0.011881 0.083659 0.55115 0.5264 0.46468
Senior_Employees 0.26425 -0.38059 -0.01066 0.038314 0.51201 0.0029976 0.99903 0.00078372
Junior_Employees 0.45596 0.23295 0.057744 0.026269 0.33097 0.15177 0.94193 0.057876
Secretaries 0.12953 -0.20109 0.078911 0.006053 0.070064 0.080522 0.86535 0.13326
Overview COLUMN POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
_______ ________ _________ _________ _____________ _____________ _____________ _____________
None 0.31606 -0.39331 -0.030492 0.049186 0.654 0.029336 0.99402 0.0059745
Light 0.23316 0.099456 0.14106 0.0070588 0.03085 0.46317 0.32673 0.65729
Medium 0.32124 0.19632 0.0073591 0.01261 0.16562 0.0017368 0.98185 0.0013796
Heavy 0.12953 0.29378 -0.19777 0.016335 0.14954 0.50575 0.6844 0.31015
-----------------------------------------------------------
Legend
Row scores in principal coordinates
Column scores in principal coordinates
CntrbPnt2In = relative contribution of points to explain total Inertia of the latent dimension
The sum of the numbers in a column is equal to 1
CntrbDim2In = relative contribution of latent dimension to explain total Inertia of a point
CntrbDim2In_1+CntrbDim2In_2+...+CntrbDim2In_K=1
Related Examples
 CorAna with supplementary rows and supplementary columns.
CorAna with supplementary rows and supplementary columns.
 CorAna with supplementary rows and supplementary columns.
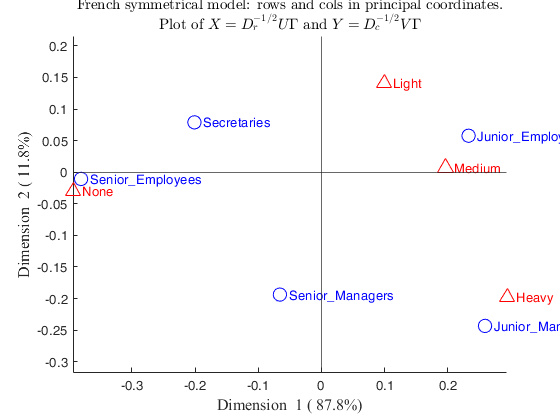
CorAna with supplementary rows and supplementary columns.Children data Active rows = 1:15 Active columns = 1:5
N=[51 64 32 29 17 59 66 70;
53 90 78 75 22 115 117 86;
71 111 50 40 11 79 88 177;
1 7 5 5 4 9 8 5;
7 11 4 3 2 2 17 18;
7 13 12 11 11 18 19 17;
21 37 14 26 9 14 34 61;
12 35 19 6 7 21 30 28;
10 7 7 3 1 8 12 8;
4 7 7 6 2 7 6 13;
8 22 7 10 5 10 27 17;
25 45 38 38 13 48 59 52;
18 27 20 19 9 13 29 53;
35 61 29 14 12 30 63 58;
2 4 3 1 4 nan nan nan ;
2 8 2 5 2 nan nan nan;
1 5 4 6 3 nan nan nan;
3 3 1 3 4 nan nan nan];
% rowslab = cell containing row labels
rowslab={'money','future','unemployment','circumstances',...
'hard','economic','egoism','employment','finances',...
'war','housing','fear','health','work','comfort','disagreement',...
'world','to_live'};
% colslab = cell containing column labels
colslab={'unqualified','cep','bepc','high_school_diploma','university',...
'thirty','fifty','more_fifty'};
tableN=array2table(N,'VariableNames',colslab,'RowNames',rowslab);
% Extract just active rows and active columns
Nactive=tableN(1:14,1:5);
% Define tables containing supplementary rows and supplementary cols
Nsupr=tableN(15:18,1:5);
Nsupc=tableN(1:14,6:8);
Sup=struct;
Sup.r=Nsupr;
Sup.c=Nsupc;
out=CorAna(Nactive,'Sup',Sup);Summary
Singular_value Inertia Accounted_for Cumulative
______________ _________ _____________ __________
dim_1 0.18815 0.035402 0.57043 0.57043
dim_2 0.11452 0.013115 0.21132 0.78175
dim_3 0.085447 0.0073011 0.11764 0.89939
dim_4 0.079018 0.0062439 0.10061 1
ROW POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
money -0.11527 0.045499 0.42845
future 0.17645 0.17567 0.71562
unemployment -0.21223 0.22616 0.87492
circumstances 0.40092 0.062745 0.58397
hard -0.24998 0.029938 0.88369
economic 0.35396 0.12005 0.48362
egoism 0.059889 0.0068096 0.073339
employment -0.13675 0.026215 0.1643
finances -0.237 0.027904 0.27623
war 0.21682 0.021688 0.74907
housing -0.006681 4.1183e-05 0.00072894
fear 0.20335 0.11666 0.90069
health 0.11165 0.020571 0.79911
work -0.21168 0.12005 0.75402
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
__________ ___________ ___________
money -0.020046 0.0037146 0.012958
future 0.097863 0.14587 0.22013
unemployment 0.070718 0.067786 0.097145
circumstances -0.33099 0.11544 0.398
hard -0.06765 0.0059184 0.064717
economic -0.32072 0.26604 0.39705
egoism 0.025667 0.0033763 0.013471
employment -0.21539 0.17555 0.4076
finances 0.20598 0.056902 0.20867
war 0.074663 0.0069419 0.088821
housing -0.12824 0.04096 0.26858
fear 0.058068 0.025678 0.073446
health -0.0042912 8.2025e-05 0.0011804
work -0.10888 0.085745 0.19951
COLUMN POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
________ ___________ ___________
unqualified -0.20932 0.2511 0.67619
cep -0.13858 0.18297 0.64492
bepc 0.10876 0.067579 0.3119
high_school_diploma 0.27404 0.37976 0.75817
university 0.23123 0.11859 0.31171
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
unqualified 0.080727 0.10082 0.10058
cep -0.056047 0.080794 0.10549
bepc 0.028483 0.012512 0.021393
high_school_diploma 0.12134 0.20099 0.14865
university -0.31786 0.60488 0.589
-----------------------------------------------------------
Overview ROW POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
________ _________ __________ __________ _____________ _____________ _____________ _____________
money 0.12123 -0.11527 -0.020046 0.0037595 0.045499 0.0037146 0.42845 0.012958
future 0.19975 0.17645 0.097863 0.0086904 0.17567 0.14587 0.71562 0.22013
unemployment 0.17776 -0.21223 0.070718 0.0091512 0.22616 0.067786 0.87492 0.097145
circumstances 0.013819 0.40092 -0.33099 0.0038038 0.062745 0.11544 0.58397 0.398
hard 0.01696 -0.24998 -0.06765 0.0011994 0.029938 0.0059184 0.88369 0.064717
economic 0.03392 0.35396 -0.32072 0.0087874 0.12005 0.26604 0.48362 0.39705
egoism 0.067211 0.059889 0.025667 0.0032871 0.0068096 0.0033763 0.073339 0.013471
employment 0.049623 -0.13675 -0.21539 0.0056484 0.026215 0.17555 0.1643 0.4076
finances 0.017588 -0.237 0.20598 0.0035763 0.027904 0.056902 0.27623 0.20867
war 0.016332 0.21682 0.074663 0.001025 0.021688 0.0069419 0.74907 0.088821
housing 0.032663 -0.006681 -0.12824 0.0020001 4.1183e-05 0.04096 0.00072894 0.26858
fear 0.099874 0.20335 0.058068 0.0045852 0.11666 0.025678 0.90069 0.073446
health 0.058417 0.11165 -0.0042912 0.00091131 0.020571 8.2025e-05 0.79911 0.0011804
work 0.094849 -0.21168 -0.10888 0.0056364 0.12005 0.085745 0.75402 0.19951
Overview COLUMN POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
________ ________ _________ _________ _____________ _____________ _____________ _____________
unqualified 0.20289 -0.20932 0.080727 0.013146 0.2511 0.10082 0.67619 0.10058
cep 0.33731 -0.13858 -0.056047 0.010044 0.18297 0.080794 0.64492 0.10549
bepc 0.20226 0.10876 0.028483 0.0076704 0.067579 0.012512 0.3119 0.021393
high_school_diploma 0.17902 0.27404 0.12134 0.017732 0.37976 0.20099 0.75817 0.14865
university 0.078518 0.23123 -0.31786 0.013468 0.11859 0.60488 0.31171 0.589
-----------------------------------------------------------
Legend
Row scores in principal coordinates
Column scores in principal coordinates
CntrbPnt2In = relative contribution of points to explain total Inertia of the latent dimension
The sum of the numbers in a column is equal to 1
CntrbDim2In = relative contribution of latent dimension to explain total Inertia of a point
CntrbDim2In_1+CntrbDim2In_2+...+CntrbDim2In_K=1
 Example of interpretation of values close to the center.
Example of interpretation of values close to the center.
 Example of interpretation of values close to the center.
Example of interpretation of values close to the center.
N=[80 20 90 90 5 100 40 50 40 40 70 10 100 40 10 70 20 90 80 99 40 0 80 2 20 95 20 40 35 52 38 47 48 80 40]; rl=["Dog" "Cat" "Rat" "Cockroach" "Wallaby"]; cl=["Big" "Athletic" "Friendly" "Trainable" "Resourceful" "Animal" "Lucky"]; Ntable=array2table(N,"RowNames",rl,"VariableNames",cl); out=CorAna(Ntable); % In the center of the map, we have Wallaby and Lucky. Does this mean % wallabies are lucky animals? No. Wallaby is pretty average on all the % variables being measured. As it has nothing that differentiates it, the % result is that it is in the middle of the map (i.e., near the origin). % Similarly, Lucky does not differentiate, so it is also near the center. % That they are both in the center tells us that they are both indistinct, % and that is all that they have in common (in the data).
Summary
Singular_value Inertia Accounted_for Cumulative
______________ _________ _____________ __________
dim_1 0.50576 0.2558 0.89448 0.89448
dim_2 0.14914 0.022243 0.077779 0.97226
dim_3 0.081626 0.0066627 0.023299 0.99556
dim_4 0.03564 0.0012702 0.0044417 1
ROW POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
________ ___________ ___________
Dog -0.59431 0.3295 0.94186
Cat -0.3256 0.081449 0.81272
Rat 0.27706 0.068913 0.57861
Cockroach 0.95997 0.51987 0.96141
Wallaby 0.019153 0.00027378 0.033895
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
Dog -0.12157 0.15856 0.039411
Cat 0.079165 0.055371 0.048044
Rat 0.22533 0.52422 0.38272
Cockroach -0.18988 0.23391 0.037614
Wallaby -0.057062 0.027946 0.30085
COLUMN POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
________ ___________ ___________
Big -0.68224 0.17879 0.90397
Athletic 0.54545 0.1711 0.97126
Friendly -0.60693 0.15363 0.86806
Trainable -0.19488 0.026427 0.47685
Resourceful 0.89767 0.42097 0.98264
Animal -0.2172 0.041317 0.59767
Lucky 0.13298 0.0077629 0.55129
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
_________ ___________ ___________
Big -0.21116 0.19698 0.086599
Athletic -0.042213 0.011785 0.0058171
Friendly -0.20525 0.20206 0.099279
Trainable 0.17768 0.25264 0.3964
Resourceful -0.072334 0.031435 0.0063805
Animal 0.16308 0.26789 0.33696
Lucky -0.08585 0.03721 0.22978
-----------------------------------------------------------
Overview ROW POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
_______ ________ _________ _________ _____________ _____________ _____________ _____________
Dog 0.23863 -0.59431 -0.12157 0.089486 0.3295 0.15856 0.94186 0.039411
Cat 0.19652 -0.3256 0.079165 0.025635 0.081449 0.055371 0.81272 0.048044
Rat 0.22965 0.27706 0.22533 0.030465 0.068913 0.52422 0.57861 0.38272
Cockroach 0.1443 0.95997 -0.18988 0.13832 0.51987 0.23391 0.96141 0.037614
Wallaby 0.1909 0.019153 -0.057062 0.0020661 0.00027378 0.027946 0.033895 0.30085
Overview COLUMN POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
________ ________ _________ _________ _____________ _____________ _____________ _____________
Big 0.098259 -0.68224 -0.21116 0.050593 0.17879 0.19698 0.90397 0.086599
Athletic 0.14711 0.54545 -0.042213 0.045062 0.1711 0.011785 0.97126 0.0058171
Friendly 0.10668 -0.60693 -0.20525 0.04527 0.15363 0.20206 0.86806 0.099279
Trainable 0.17799 -0.19488 0.17768 0.014176 0.026427 0.25264 0.47685 0.3964
Resourceful 0.13363 0.89767 -0.072334 0.10958 0.42097 0.031435 0.98264 0.0063805
Animal 0.22403 -0.2172 0.16308 0.017683 0.041317 0.26789 0.59767 0.33696
Lucky 0.1123 0.13298 -0.08585 0.0036019 0.0077629 0.03721 0.55129 0.22978
-----------------------------------------------------------
Legend
Row scores in principal coordinates
Column scores in principal coordinates
CntrbPnt2In = relative contribution of points to explain total Inertia of the latent dimension
The sum of the numbers in a column is equal to 1
CntrbDim2In = relative contribution of latent dimension to explain total Inertia of a point
CntrbDim2In_1+CntrbDim2In_2+...+CntrbDim2In_K=1
Input Arguments
N — Contingency table (default) or n-by-2 input dataset.
2D Array or Table.
2D array or table or timetable which contains the input contingency table (say of size I-by-J) or the original data matrix X.
In this last case N=crosstab(X(:,1),X(:,2)), as default procedure assumes that the input is a contingency table.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'k',3
, 'Lr',{'a' 'b' 'c'}
, 'Lc',{'c1' c2' 'c3' 'c4'}
, 'Sup', Sup=struct; Sup.c={'c2' 'c4'}
, 'datamatrix',true
, 'plots',1
, 'dispresults',false
, 'd1',2
, 'd2',3
k
—Number of dimensions to retain.scalar.
Scalar which contains the number of dimensions to retain.
The default value of k is 2.
Example: 'k',3
Data Types: double
Lr
—Vector of row labels.cell.
Cell containing the labels of the rows of the input contingency matrix N. This option is unnecessary if N is a table, because in this case Lr=N.Properties.RowNames;
Example: 'Lr',{'a' 'b' 'c'}
Data Types: cell array of strings
Lc
—Vector of column labels.cell.
Cell containing the labels of the columns of the input contingency matrix N. This option is unnecessary if N is a table, because in this case Lc=N.Properties.VariableNames;
Example: 'Lc',{'c1' c2' 'c3' 'c4'}
Data Types: cell array of strings
Sup
—Structure containing indexes or names of supplementary rows
or columns.structure.
Structure with the following fields.
| Value | Description |
|---|---|
r |
vector containing row indexes or vector of cell array of strings or table or 2D numeric array, containing supplementary rows. If indexes or cell array of strings are supplied in a vector, we assume that supplementary rows belong to contingency table N. For example: - if Sup.r=[2 5] (that is, Sup.r is a numeric vector which contains row indexes) we use rows 2 and 5 of the input contingency table as supplementary rows. - if Sup.r={'Junior-Managers' 'Senior-Employees'} (that is, Sup.r is a cell array of strings) we use rows named 'Junior-Managers' and 'Senior-Employees' of the input contingency table as supplementary rows. Of course the length of Sup.r must be smaller than the number of rows of the contingency matrix divided by 2. - if Sup.r is a table, or a 2D array, supplementary rows do not belong to N. Note that if Sup.r is a table, the labels of the rows are taken directly from the table. If, on the other hand, Sup.r is a matrix, the names of the rows of the supplementary units can be given using Sup.Lr as a cell array of strings. |
Lr |
cell array of strings containing the labels of the supplementary units if Sup.r is a 2D numeric array. |
c |
vector containing column indexes or vector of cell array of strings or table or 2D numeric array used as supplementary columns, or table or 2D numeric array containing supplementary rows. If indexes or cell array of strings are supplied in a vector, we assume that supplementary columns belong to contingency table N. For example: - If Sup.c = [2 3] (that is, Sup.c is a numeric vector that contains column indexes), we use columns 2 and 3 of the input contingency table as supplementary columns. - If Sup.c = {'Smokers' 'NonSmokers'} (that is, Sup.c is a cell array of strings), we use columns of the contingency table labeled 'Smokers' and 'NonSmokers' of the input contingency table N as supplementary columns. Of course the length of Sup.c must be smaller than the number of columns of the contingency matrix divided by 2. - If Sup.c is a table, or a 2D array, supplementary columns do not belong to N. Note that if Sup.c is a table, the labels of the columns are taken directly from the table. If, on the other hand, Sup.c is a matrix, the names of the columns of the supplementary units can be given using Sup.Lc as a cell array of strings. |
Lc |
cell array of strings containing the labels of the supplementary units, if Sup.c is a 2D numeric array. REMARK: The default value of Sup is a missing value; that is, we assume that there are no supplementary rows or columns. |
Example: 'Sup', Sup=struct; Sup.c={'c2' 'c4'}
Data Types: struct
datamatrix
—Data matrix or contingency table.boolean.
If datamatrix is true, the first input argument N is forced to be interpreted as a data matrix; else, if the input argument is false, N is treated as a contingency table. The default value of datamatrix is false; that is, the procedure automatically considers N as a contingency table (in array or table format). If datamatrix is true, N can be an array or a table of size n-by-2. Note that if N has more than two columns, correspondence analysis is based on the first two columns of N (and a warning is produced).
Example: 'datamatrix',true
Data Types: logical
plots
—Plot on the screen.scalar | structure.
If plots = 1, a plot that shows the principal coordinates of rows and columns is shown on the screen. If plots is a structure, it may contain the following fields:
| Value | Description |
|---|---|
alpha |
type of plot, scalar in the interval [0 1] or a string identifying the type of coordinates to use in the plot. If $plots.alpha='rowprincipal'$ the row points are in principal coordinates and the column coordinates are standard coordinates. Distances between row points are (approximated) chi-squared distances (row-metric-preserving). The position of the row points is at the weighted average of the column points. Note that 'rowprincipal' can also be specified by setting plots.alpha=1. If $plots.alpha='colprincipal'$, the column coordinates are referred to as principal coordinates and the row coordinates as standard coordinates. Distances between column points are (approximated) chi-squared distances (column-metric-preserving). The position of the column points is at the weighted average of the row points. Note that 'colprincipal' can also be specified by setting plots.alpha=0. If $plots.alpha='symbiplot'$, the row and column coordinates are scaled similarly. The sum of weighted squared coordinates for each dimension is equal to the corresponding singular values. These coordinates are often called symmetrical coordinates. This representation is particularly useful if one is primarily interested in the relationships between categories of row and column variables rather than in the distances among rows or among columns. 'symbiplot' can also be specified by setting plots.alpha=0.5; If $plots.alpha='bothprincipal'$, both the rows and columns are depicted in principal coordinates. Such a plot is often referred to as a symmetrical plot or French symmetrical model. Note that such a symmetrical plot does not provide a feasible solution in the sense that it does not approximate matrix $D_r^{-0.5}(P-rc')D_c^{-0.5}$. |
FontSize |
scalar, which specifies the font size of row (column) labels. The default value is 10. |
MarkerSize |
scalar, which specifies the marker size of symbols associated with rows or columns. The default value is 10. |
Example: 'plots',1
Data Types: scalar double | struct
dispresults
—Display results on the screen.boolean.
If dispresults is true (default), it is possible to see on the screen all the summary results of the analysis.
Example: 'dispresults',false
Data Types: Boolean
d1
—Dimension to show on the horizontal axis.positive integer.
Positive integer in the range 1, 2, .., K which indicates the dimension to show on the x axis. The default value of d1 is 1.
Example: 'd1',2
Data Types: single | double
d2
—Dimension to show on the vertical axis.positive integer.
Positive integer in the range 1, 2, .., K which indicates the dimension to show on the y axis. The default value of d2 is 2.
Example: 'd2',3
Data Types: single | double
Output Arguments
out — description
Structure
A structure containing the following fields:
| Value | Description |
|---|---|
Lr |
cell of length $I$ containing the labels of active rows (i.e., the rows that participated in the fit). |
Lc |
cell of length $J$ containing the labels of active columns (i.e., the columns that participated in the fit). |
N |
$I$-by-$J$-array containing contingency table referred to active rows and active columns (i.e., referred to the rows/columns that participated in the fit). The $(i,j)$-th element is equal to $n_{ij}$, $i=1, 2, \ldots, I$ and $j=1, 2, \ldots, J$. The sum of the elements of out.P is $n$ (the grand total). |
Ntable |
Same as out.N, but in table format (with row and column names). This output is present just if your MATLAB version is not<2013b. |
I |
Number of active rows of contingency table. |
J |
Number of active columns of contingency table. |
n |
Grand total. out.n is equal to sum(sum(out.N)). This is the number of observations. |
Nhat |
$I$-by-$J$-array containing contingency table referred to active rows (i.e., referred to the rows that participated in the fit) under the independence hypothesis. The $(i,j)$-th element is equal to $n_{i.}n_{.j}/n$, $i=1, 2, \ldots, I$ and $j=1, 2, \ldots, J$. The sum of the elements of out.Nhat is $n$ (the grand total). |
Nhattable |
Same as out.Nhat, but in table format (with row and column names). |
P |
$I$-by-$J$-array containing correspondence matrix (proportions). The $(i,j)$-th element is equal to $n_{ij}/n$, $i=1, 2, \ldots, I$ and $j=1, 2, \ldots, J$. The sum of the elements of out.P is 1. |
Ptable |
Same as out.P, but in table format (with row and column names). This output is present just if your MATLAB version is not<2013b. |
r |
Vector of length $I$ containing row masses. \[ r=(f_{1.}, f_{2.}, \ldots, f_{I.})' \] $r$ is also the centroid of column profiles. |
Dr |
Square matrix of size $I$ containing on the diagonal the row masses. This is matrix $D_r$. \[ D_r=diag(r) \] |
c |
Vector of length $J$ containing column masses. \[ c=(f_{.1}, f_{.2}, \ldots, f_{.J})' \] $c$ is also the centroid of row profiles. |
Dc |
Square matrix of size $J$ containing on the diagonal the column masses. This is matrix $D_c$. \[ D_c=diag(c) \] |
ProfilesRows |
$I$-by-$J$-matrix containing row profiles. The $i,j$-th element of this matrix is given by $f_{ij}/f_{i.}=n_{ij}/n_{i.}$. Written in matrix form: \[ ProfilesRows = D_r^{-1} \times P \] |
ProfilesCols |
$I$-by-$J$-matrix containing column profiles. The $i,j$-th element of this matrix is given by $f_{ij}/f_{.j}=n_{ij}/n_{.j}$. Written in matrix form: \[ ProfilesCols = P \times D_c^{-1} \] |
K |
Scalar integer containing the maximum number of dimensions. $K = \min(I-1,J-1)$. |
k |
Scalar integer containing the number of retained dimensions. |
Residuals |
$I$-by-$J$-matrix containing standardized residuals. \[ Residuals = D_r^{1/2} (D_r^{-1} P - r c') D_c^{-1/2} = D_r^{-1/2} (P - r c') D_c^{-1/2} \] With the singular value decomposition (SVD) we obtain that: \[ Residuals = U \Gamma V' \] |
TotalInertia |
Scalar containing total inertia. Total inertia is equal (for example) to the sum of the squares of the elements of matrix out.Residuals. |
Chi2stat |
Scalar containing Chi-square statistic for the contingency table. $Chi2stat= TotalInertia \times n$. |
CramerV |
Scalar containing Cramer's $V$ index. \[ V=\sqrt{Chi2stat/(n (\min(I,J)-1))} \] Cramer's index goes between 0 and 1. |
InertiaExplained |
matrix with 4 columns. - First column contains the singular values (the sum of the squared singular values is the total inertia). - Second column contains the eigenvalues (the sum of the eigenvalues is the total inertia). - Third column contains the variance explained by each latent dimension. - Fourth column contains the cumulative variance explained by each dimension. |
RowsPri |
$I$-by-$K$ matrix containing principal coordinates of rows. \[ RowsPri = D_r^{-1/2} \times U \times \Gamma; \] |
ColsPri |
$J$-by-$K$ matrix containing Principal coordinates of columns. \[ ColsPri = D_c^{-1/2} \times V \times \Gamma; \] |
RowsSta |
$I$-by-$K$ matrix containing standard coordinates of rows. \[ RowsSta = RowsPri \times \Gamma^{-1} = D_r^{-1/2} U \Gamma \Gamma^{-1}= D_r^{-1/2} U \] |
ColsSta |
$J$-by-$K$ matrix containing standard coordinates of columns. \[ ColsSta = ColsPri \times \Gamma^{-1} = D_c^{-1/2} V \Gamma \Gamma^{-1}= D_c^{-1/2} V \] |
RowsSym |
$I$-by-$K$ matrix containing symmetrical coordinates of rows. \[ RowsSym = D_r^{-1/2} \times U \times \Gamma^{1/2} \] |
ColsSym |
$J$-by-$K$ matrix containing symmetrical coordinates of columns. \[ ColsSym = D_c^{-1/2} \times V \times \Gamma^{1/2} \] Symmetric plot represents the row and column profiles simultaneously in a common space (Bendixen, 2003). In this case, only the distance between row points or the distance between column points can be really interpreted. The distance between any row and column items is not meaningful! You can only make general statements about the observed pattern. In order to interpret the distance between column and row points, the column profiles must be presented in row space or vice versa. This type of map is called asymmetric biplot. |
InertiaRows |
$I$-by-$2$ matrix containing absolute and relative contribution of each row to total inertia. The inertia of a point is the squared distance of point $d_i^2$ to the centroid. The absolute contribution of a point to total inertia is the inertia of the point multiplied by the point mass. 1st column = absolute contribution of each row to TotalInertia. The sum of values of the first column is equal to TotalInertia; 2nd column = relative contribution of each row to TotalInertia. The sum of the values of the second column is equal to 1. |
InertiaCols |
$J$-by-$2$ matrix containing absolute and relative contribution of each column to total inertia. The inertia of a point is the squared distance of point $d_i^2$ to the centroid. The absolute contribution of a point to total inertia is the inertia of the point multiplied by the point mass. 1st column = absolute contribution of each column to TotalInertia. The sum of values of the first column is equal to TotalInertia; 2nd column = relative contribution of each column to TotalInertia. The sum of values of the second column is equal to 1. |
Point2InertiaRows |
$I$-by-$K$ matrix containing relative contributions of rows to inertia of the dimension. The inertia of first latent dimension is given by $\lambda_1=\gamma_{11}^2$. The inertia of second latent dimension is given by $\lambda_2=\gamma_{22}^2$ .... The sum of each column of matrix Point2InertiaRows is equal to 1. Remark: the points with the larger value of Point2Inertia are those that contribute the most to the definition of the dimension. If the row contributions were uniform, the expected value would be 1/size(contingeny_table,1). For a given dimension, any row with a contribution larger than this threshold could be considered as important in contributing to that dimension. |
Point2InertiaCols |
$J$-by-$K$ matrix containing relative contributions of columns to inertia of the dimension. The sum of each column of matrix Point2InertiaCols is equal to 1. |
Dim2InertiaRows |
$I$-by-$K$ matrix containing relative contributions of latent dimensions to the inertia of the row points. These numbers can be interpreted as squared correlations and measure the degree of association between row points and a particular axis. The sum of each row of matrix Dim2InertiaRows is equal to 1. |
Dim2InertiaCols |
$J$-by-$K$ matrix containing relative contributions of latent dimensions to the inertia of the column points. These numbers can be interpreted as squared correlations and measure the degree of association between columns points and a particular axis. The sum of each row of matrix Dim2InertiaCols is equal to 1. |
cumsumDim2InertiaRows |
$I$-by-$K$ matrix containing cumulative sum of the contributions of latent dimensions to the inertia of the row points. These cumulative sums are equivalent to the communalities in PCA. The last column of matrix cumsumDim2InertiaRows is equal to 1. |
cumsumDim2InertiaCols |
$J$-by-$K$ matrix containing cumulative sum of the contributions of latent dimensions to the inertia of the column points. These cumulative sums are equivalent to the communalities in PCA. The last column of matrix cumsumDim2InertiaCols is equal to 1. |
sqrtDim2InertiaRows |
$I$-by-$K$ matrix containing correlation of rows points with latent dimension axes. Similar to component loadings in PCA. |
sqrtDim2InertiaCols |
$I$-by-$K$ matrix containing correlation of column points with latent dimension axes. Similar to component loadings in PCA. |
Summary |
$K$-times-4 table containing summary results for correspondence analysis. First column contains the singular values (the sum of the squared singular values is the total inertia). Second column contains the eigenvalues (the sum of the eigenvalues is the total inertia). Third column contains the variance explained by each latent dimension. Fourth column contains the cumulative variance explained by each dimension. This output is present just if your MATLAB version is not<2013b. |
OverviewRows |
$I$-times-(k*3+2) table containing an overview of row points. More precisely, if we suppose that $k=2$, First column contains the row masses (vector $r$). The second column contains the scores of the first dimension. The third column contains the scores of the second dimension. The fourth column contains the inertia of each point, where the inertia of a point is the squared distance of point $d_i^2$ to the centroid. The fifth column contains the relative contribution of each point to the explanation of the inertia of the first dimension. The sum of the elements of this column is equal to 1. The sixth column contains the relative contribution of each point to the explanation of the inertia of the second dimension. The sum of the elements of this column is equal to 1. The seventh column contains the relative contribution of the first dimension to the explanation of the inertia of the point. The eighth column contains the relative contribution of the second dimension to the explanation of the inertia of the point. |
OverviewCols |
$J$-times-(k*3+2) table containing an overview of row points. More precisely if we suppose that $k=2$ First column contains the column masses (vector $c$). The second column contains the scores of the first dimension. The third column contains the scores of the second dimension. The fourth column contains the inertia of each point, where the inertia of a point is the squared distance of point $d_i^2$ to the centroid. The fifth column contains the relative contribution of each point to the explanation of the inertia of the first dimension. The sum of the elements of this column is equal to 1. The sixth column contains the relative contribution of each point to the explanation of the inertia of the second dimension. The sum of the elements of this column is equal to 1. The seventh column contains the relative contribution of the first dimension to the explanation of the inertia of the point. The eighth column contains the relative contribution of the second dimension to the explanation of the inertia of the point. |
LrSup |
cell containing the labels of the supplementary rows (i.e. the rows which did not participate to the fit). |
LcSup |
cell containing the labels of supplementary columns (i.e. the columns which did not participate to the fit). |
SupRowsN |
matrix of size length(LrSup)-by-c referred to supplementary rows. If there are no supplementary rows this field is not present. |
SupRowsNtable |
Same as out.SupRowsN but in table format (with row and column names). This is the contingency table referred to supplementary rows. If there are no supplementary rows this field is not present. This output is present just if your MATLAB version is not<2013b. |
SupColsN |
matlab of size r-by-length(LcSup) referred to supplementary columns. If there are no supplementary columns this field is not present. |
SupColsNtable |
Same as out.SupColsN but in table format (with row and column names). This is the contingency table referred to supplementary columns. If there are no supplementary columns this field is not present. This output is present just if your MATLAB version is not<2013b. |
RowsPriSup |
Principal coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
RowsStaSup |
Standard coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
RowsSymSup |
Symmetrical coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
ColsPriSup |
Principal coordinates of supplementary columns. If there are no supplementary columns this field is not present. |
ColsStaSup |
Standard coordinates of of supplementary columns. If there are no supplementary columns this field is not present. |
ColsSymSup |
Symmetrical coordinates of supplementary columns. If there are no supplementary columns this field is not present. |
References
Benzecri, J.-P. (1992), "Correspondence Analysis Handbook", New-York, Dekker.
Benzecri, J.-P. (1980), "L'analyse des donnees tome 2: l'analyse des correspondances", Paris, Bordas.
Greenacre, M.J. (1993), "Correspondence Analysis in Practice", London, Academic Press.
Gabriel, K.R. and Odoroff, C. (1990), Biplots in biomedical research, "Statistics in Medicine", Vol. 9, pp. 469-485.
Greenacre, M.J. (1993), Biplots in correspondence Analysis, "Journal of Applied Statistics", Vol. 20, pp. 251-269.
Riani, M, Atkinson A.C., Torti, F., Corbellini A. (2023), Robust Correspondence Analysis, "Journal of the Royal Statistical Society Series C: Applied Statistics", Vol. 71, pp. 1381–1401, https://doi.org/10.1111/rssc.12580
Acknowledgements
This function has been inspired by the code developed by: Urbano Lorenzo-Seva (Rovira i Virgili University, Tarragona, Spain), Michel van de Velden (Erasmus University, Rotterdam, The Netherlands), and Henk A.L. Kiers (University of Groningen, Groningen, The Netherlands) (See References).
See Also
crosstab
|
rcontFS
|
CressieRead
|
CorAnaplot