FSMinvmmd
FSMinvmmd converts values of minimum Mahalanobis distance into confidence levels
Description
Examples
FSMinvmmd with all default options.
After creating 99 per cent confidence envelopes based on 1000 observations and 5 variables are created, their confidence level is calculated with FSMinvmmd.
v=5; mmdenv=FSMenvmmd(1000,v,'prob',0.99); mmdinv=FSMinvmmd(mmdenv,v); % mmdinv is a matrix which in the second colum contains % all values equal to 0.99.
FSMinvmmd with optional arguments.
Example of finding confidence level of mmd. Forgery Swiss Banknotes data.
load('swiss_banknotes');
Y=swiss_banknotes{:,:};
Y=Y(101:200,:);
% The line below shows the plot of mmd
[out]=FSM(Y,'plots',1);
% The line below transforms the values of mmd into observed confidence
% levels and shows the output in a plot in normal coordinates using all
% default options
plots=struct;
plots.conflev=[0.01 0.5 0.99 0.999 0.9999 0.99999];
mmdinv=FSMinvmmd(out.mmd,size(Y,2),'plots',plots);
Related Examples
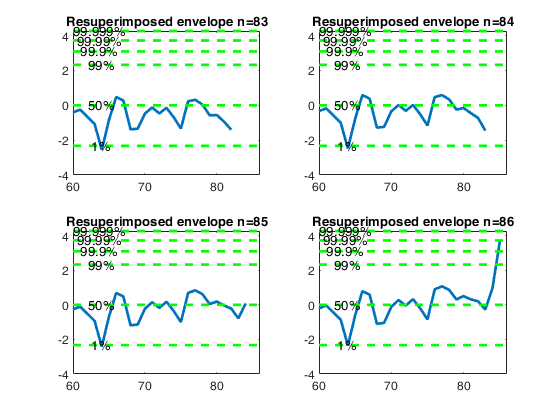
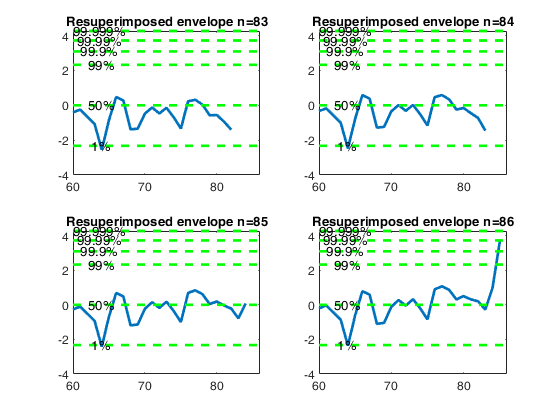
 Resuperimposing envelopes and normal coordinates.
Resuperimposing envelopes and normal coordinates.
 Resuperimposing envelopes and normal coordinates.
Resuperimposing envelopes and normal coordinates.Comparison of resuperimposing envelopes using mmd coordinates and normal coordinates. Forgery Swiss Banknotes data.
load('swiss_banknotes');
Y=swiss_banknotes{:,:};
Y=Y(101:200,:);
% The line below shows the plot of mmd
[out]=FSM(Y,'plots',2);
n0=83:86;
quantplo=[0.01 0.5 0.99 0.999 0.9999 0.99999];
ninv=norminv(quantplo);
lwdenv=2;
supn0=max(n0);
ij=0;
for jn0=n0;
ij=ij+1;
MMDinv = FSMinvmmd(out.mmd,size(Y,2),'n',jn0);
% Resuperimposed envelope in normal coordinates
subplot(2,2,ij)
plot(MMDinv(:,1),MMDinv(:,3),'LineWidth',2)
xlim([out.mmd(1,1) supn0])
v=axis;
line(v(1:2)',[ninv;ninv],'color','g','LineWidth',lwdenv,'LineStyle','--','Tag','env');
text(v(1)*ones(length(quantplo),1),ninv',strcat(num2str(100*quantplo'),'%'));
title(['Resuperimposed envelope n=' num2str(jn0)]);
end-------------------------
Signal detection loop
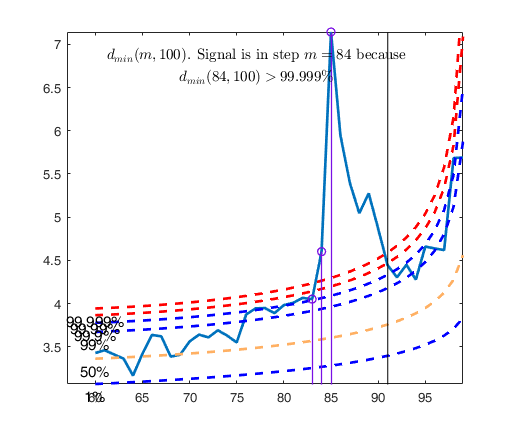
Tentative signal in central part of the search: step m=84 because
dmin(84,100)>99.999%
-------------------
Signal validation
Validated signal
-------------------------------
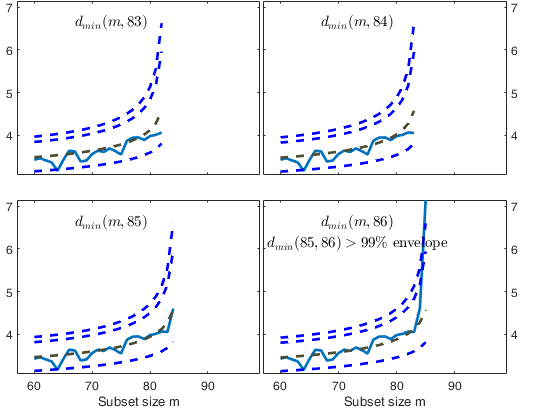
Start resuperimposing envelopes from step m=83
Superimposition stopped because d_{min}(85,86)>99% envelope
$d_{min}(85,86)>99$\% envelope
----------------------------
Final output
Number of units declared as outliers=15
Summary of the exceedances
1 99 999 9999 99999
0 21 15 7 7
Input Arguments
mmd — Distances.
Matrix.
n-m0 x 2 matrix.
1st col = fwd search index;
2nd col = minimum Mahalanobis distance.
Data Types: single | double
v — Number of variables.
Scalar.
Number of variables of the underlying dataset.
Data Types: single | double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'n',5
, 'plots',1
n
—It specifies the size of the sample.scalar.
If it is not specified it is set equal to mmd(end,1)+1.
Example: 'n',5
Data Types: double
plots
—Plot on the screen.scalar | structure.
If plots = 1, a plot which shows the confidence level of mmd in each step is shown on the screen. Three horizontal lines associated respectively with values 0.01, 0.5 and 0.99 are added to the plot.
If plots is a structure, it may contain the following fields:
| Value | Description |
|---|---|
conflev |
vector containing horizontal lines associated with confidence levels; |
conflevlab |
scalar if it is equal 1 labels associated with horizontal lines are shown on the screen; |
xlim |
minimum and maximum on the x axis; |
ylim |
minimum and maximum on the y axis; |
LineWidth |
Line width of the trajectory of mmd in normal coordinates; |
LineStyle |
Line style of the trajectory of mle of transformation parameters; |
LineWidthEnv |
Line width of the horizontal lines; |
Tag |
tag of the plot (default is pl_mmdinv); |
FontSize |
font size of the text labels which identify the trajectories |
Example: 'plots',1
Data Types: double
Output Arguments
mmdinv —confidence levels plotted in normal coordinates.
(n-m0) -by- 3 matrix (same rows of input matrix mmd)
It contains information about requested confidence levels plotted in normal coordinates.
1st col = fwd search index from m0 to n-1;
2nd col = confidence level of each value of mmd;
3rd col = confidence level in normal coordinates.
50 per cent conf level becomes norminv(0.50)=0;
99 per cent conf level becomes norminv(0.99)=2.33.
More About
Additional Details
Let $d^2_i(m )$ and $d_{\mbox{min}}(m)$ be respectively the deletion distance for unit $i$ based on a subset of size $m$ and $d_{\mbox{min}}(m)$ the min. Mahalanobis distance in the forward search at step m. Testing for outliers requires a reference distribution for $d^2_i(m )$ in and hence for $d_{\mbox{min}}(m)$ in (\ref{min}). When $\Sigma$ is estimated from all $n$ observations, the squared statistics have an $F$ distribution.
However, the estimate $\hat{\Sigma}(m)$ in the search uses the central $m$ out of $n$ observations, so that the variability is underestimated.
The consistency factor $c(m,n)$ given below
\[ c(m,n)=\frac{n}{m} C_{v+2} \{C_{v}^{-1} (m/n) \} \]where $C_r$ is the c.d.f. of the $\chi^2$ distribution on $r$ degrees of freedom, allows for estimation from this truncated distribution, providing an approximately unbiased estimate of $\Sigma$.
We can treat the distribution of the rescaled deletion Mahalanobis distance $c(m,n)d_{\mbox{min}}^2(m)$ as a squared deletion distance on $m-1$ degrees of freedom, whose distribution is (Atkinson Riani and Cerioli, 2004; pp. 43-44) \begin{equation}\label{F} \frac{m^2-1}{m(m-v)} F_{v,m-v}, \end{equation} The distribution of the rescaled min Mahalanobis distance $c(m,n) d_{\mbox{min}}^2(m)$ of a subset of size $m$ constructed in such a way that the centroid and covariance matrix of the subset are taken using the units having the $m$ smallest Mahalanobis distances can be treated as the distribution of the $(m+1)$th order statistic from ($F_{v,m-v}$).
The results of order statistics $Y_{(1)}$, $Y_{(2)}$, $\cdots$, $Y_{(n)}$ from a sample of size $n$ from a distribution with CDF $G(y)$, state that \begin{equation} \label{orderstat} P\{Y_{(m+1)} \le y \} = P \left\{ F_{2(n-m),2(m+1)} > \frac{1-G(y)}{G(y)} \times \frac{m+1}{n-m} \right\} \end{equation} Given that in our case $G(y)$ is the CDF of the $F_{v,m-v}$ we can rewrite this equation as \begin{eqnarray*} && P\{d_{\mbox{ min}}^2(m) \leq \widehat{ d_{\mbox{min}}^2(m)} \} = \\ && 1- F_{2(n-m),2(m+1)} \left( \left( \frac{1}{ F_{v,m-v} \left( \frac{m(m-v)}{m^2-1 } c(m,n) d_{\mbox{min}}^2(m) \right) }-1 \right) \frac{m+1}{n-m} \right) \end{eqnarray*} where $F_{a,b}(y)$ is the CDF of the $F$ distribution with $a$ and $b$ degrees of freedom evaluated in $y$.
The value of the min. Mahalanobis distance transformed in normal coordinates computed by this routine is nothing but
\[ \Phi^{-1} \left( P\left\{ d_{\mbox{min}}^2(m) \leq \widehat{ d_{\mbox{min}}^2(m)} \right\} \right) \]where $\Phi^{-1}$ is the inverse of the CDF of the standard normal distribution.
References
Atkinson, A.C. and Riani, M. (2006), Distribution theory and simulations for tests of outliers in regression, "Journal of Computational and Graphical Statistics", Vol. 15, pp. 460-476.
Riani, M. and Atkinson, A.C. (2007), Fast calibrations of the forward search for testing multiple outliers in regression, "Advances in Data Analysis and Classification", Vol. 1, pp. 123-141.