FSRr

Forward search in linear regression reweighted

expand all in page

Syntax

Description

FSRr uses the units not declared by outliers by FSR to produce a robust fit.

The units whose residuals exceeds the threshold determined by option alpha are declared as outliers. Moreover, it is possible in option R2th to modify the estimate of sigma2 which is used to declare the outliers. This is useful when there is almost a perfect fit in the data, the estimate of the error variance is very small and therefore there is the risk of declaring as outliers very small deviations from the robust fit. In this case the estimate of sigma2 is corrected in order to achieve a value of R2 equal to R2th.

example

out =FSRr(y, X) Example of outlier detection in a case of almost perfect fit: all default options.

example

out =FSRr(y, X, Name, Value) Example of outlier detection in a case of almost perfect fit.

example

[out , varargout] =FSRr(___) Use of FSRr in a real dataset from international trade.

Examples

expand all

  • Example of outlier detection in a case of almost perfect fit: all default options.

    • n=200; p=1;
X = rand(n,p);
y = X + 0.01*randn(n,1);
% contaminated data points
ycont = y;
ycont(1:8) = ycont(1:8)+0.05;
[out , xnew1 , ypred1, yci1] = ...
FSRr(ycont,X,'plotsPI',1,'plots',1);
disp(['Outliers without R2 adjustment = ' num2str(out.outliers)]);
disp(['Outliers with    R2 adjustment = ' num2str(out.outliersr)]);
    Outliers without R2 adjustment = 1  2  4  5  6  7
Outliers with    R2 adjustment = 1    2    3    4    5    6    7    8   52   72  100  101  149  161  175
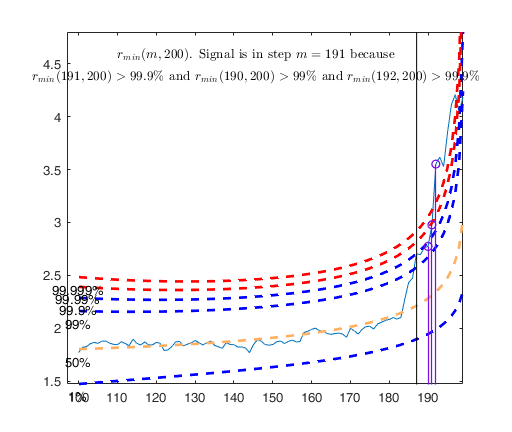
    Click here for the graphical output of this example (link to Ro.S.A. website).

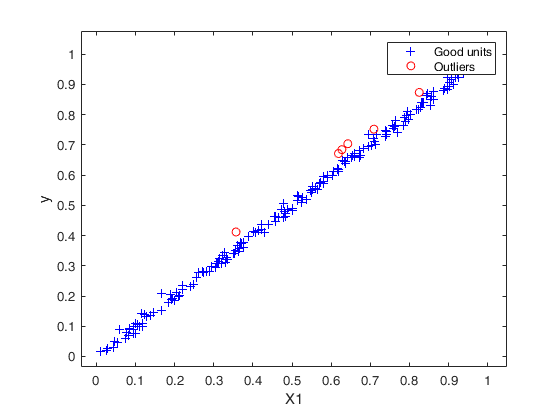
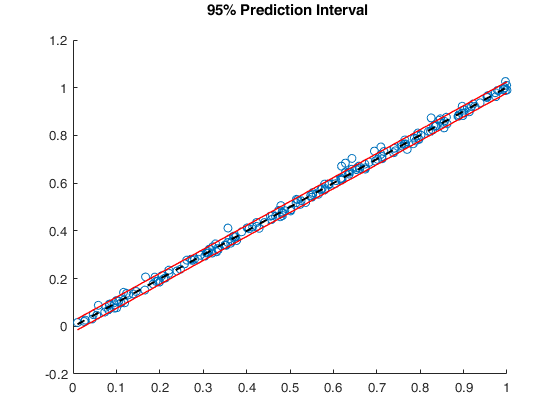
  • Example of outlier detection in a case of almost perfect fit.

    • n=200; p=1;
X = rand(n,p);
y = X + 0.01*randn(n,1);
% contaminated data points
ycont = y;
ycont(1:8) = ycont(1:8)+0.05;
[out1 , xnew1 , ypred1, yci1] = ...
FSRr(ycont,X,'alpha',0.01,...
'fullreweight',true ,'plotsPI',1,'plots',0);
h1 = allchild(gca); a1 = gca; f1 = gcf;
[out2 , xnew2 , ypred2, yci2] = ...
FSRr(ycont,X,'alpha',0.01,'R2th',0.95,...
'fullreweight',true ,'plotsPI',1,'plots',0);
h2 = allchild(gca); a2 = gca; f2 = gcf;
% move the figure above into a single one with two panels
figure; ax1 = subplot(2,1,1); ax2 = subplot(2,1,2);
copyobj(h1,ax1); title(ax1,get(get(a1,'title'),'string'));
copyobj(h2,ax2); title(ax2,get(get(a2,'title'),'string'));
close(f1); close(f2);
disp(['Outliers without R2 adjustment = ' num2str(out1.outliersr)]);
disp(['Outliers with    R2 adjustment = ' num2str(out2.outliersr)]);

  • Use of FSRr in a real dataset from international trade.

    • close all; clear all;
load fishery;
X = fishery{:,1};
y = fishery{:,2};
n = length(y);
% Bonferronized confidence level
cl = 0.005/n;
% FSRr, with scale rescaled so that R2 is forced to be 0.85 
outFSr = FSRr(y,X,'alpha',cl,'R2th',0.85,'fullreweight',true,'plotsPI',1,'plots',0);
h3 = allchild(gca); a3 = gca; f3 = gcf; set(f3,'visible','off');
% Scatter of outliers detected with R2th=0.85 
FSroutliersr = ones(n,1); FSroutliersr(outFSr.outliersr) = 0;
plo.clr = 'rb'; plo.sym = 'xo'; plo.labeladd = 1;
yXplot(y,X,'group',FSroutliersr,'plo',plo,'tag','FSrfit');
olsline(1)
price_FSr = X(logical(FSroutliersr))\y(logical(FSroutliersr));
h4 = allchild(gca); a4 = gca; f4 = gcf; set(f4,'visible','off');
% move the figures above into a single one with two panels
figure; ax3 = subplot(2,1,1); ax4 = subplot(2,1,2);
copyobj(h3,ax3); copyobj(h4,ax4); 
xlabel('Quantity-Ton','Fontsize',14); 
ylabel(ax3,'Value-1000euro','Fontsize',14);
ylabel(ax4,'Value-1000euro','Fontsize',14);
title(ax3,{'"fishery" dataset: FSRr fit with R2th=0.85','Prediction interval and outliers detected'},'Fontsize',20,'Interpreter','LaTex');
close(f3); close(f4);

    Related Examples

    expand all

  • Comparing LTS, FSR and FSRr on the international trade dataset.

    • close all;
clear all;
load fishery
X = fishery{:,1};
y = fishery{:,2};
n = length(y);
% Bonferronized confidence level
cl = 0.01/n;
% LTS with 60% observations for the LS fit
h = floor(n*0.6);
outLTS = LXS(y,X,'plots',0,'conflev',1-cl,'h',h);
plo.clr = 'rb'; plo.sym = 'xo'; plo.labeladd = 1;
yXplot(y,X,outLTS.weights,plo,'tag','LTSfit');
olsline(1)
price_LTS = X(logical(outLTS.weights))\y(logical(outLTS.weights));
title({'LTS fit using 60% of the data' , [num2str(price_LTS) ' euro/Kg']},'Fontsize',13);
xlabel('Quantity-Ton','Fontsize',14); ylabel('Value-1000euro','Fontsize',14);
h1 = allchild(gca); a1 = gca; f1 = gcf;
% Standard FSR, with Bonferronized band
outFS = FSR(y,X,'plots',0,'bonflev',cl,'h',h);
FSoutliers = ones(n,1); FSoutliers(outFS.outliers) = 0;
yXplot(y,X,'group',FSoutliers,'plo',plo,'tag','FSfit');
olsline(1)
price_FS = X(logical(FSoutliers))\y(logical(FSoutliers));
title({'Standard FS fit' , [num2str(price_FS) ' euro/Kg']},'Fontsize',13);
xlabel('Quantity-Ton','Fontsize',14); ylabel('Value-1000euro','Fontsize',14);
h2 = allchild(gca); a2 = gca; f2 = gcf;
% FSRr, with scale rescaled so that R2 is forced to be 0.9 
outFSr = FSRr(y,X,'alpha',cl,'R2th',0.90,'fullreweight',true,'plotsPI',1,'plots',0);
title({'Prediction interval for FSRr fit' , 'with R2th=0.90.'},'Fontsize',13);
xlabel('Quantity-Ton','Fontsize',14); ylabel('Value-1000euro','Fontsize',14);
h3 = allchild(gca); a3 = gca; f3 = gcf;
FSroutliersr = ones(n,1); FSroutliersr(outFSr.outliersr) = 0;
yXplot(y,X,'group',FSroutliersr,'plo',plo,'tag','FSrfit');
olsline(1)
price_FSr = X(logical(FSroutliersr))\y(logical(FSroutliersr));
title({'FSRr fit, with R2th=0.90' , [num2str(price_FSr) ' euro/Kg']},'Fontsize',13);
xlabel('Quantity-Ton','Fontsize',14); ylabel('Value-1000euro','Fontsize',14);
h4 = allchild(gca); a4 = gca; f4 = gcf;
% move the figure above into a single one with two panels
figure; ax1 = subplot(2,2,1); ax2 = subplot(2,2,2);
ax3 = subplot(2,2,3); ax4 = subplot(2,2,4);
copyobj(h1,ax1); title(ax1,get(get(a1,'title'),'string'));
copyobj(h2,ax2); title(ax2,get(get(a2,'title'),'string'));
copyobj(h3,ax3); title(ax3,get(get(a3,'title'),'string'));
copyobj(h4,ax4); title(ax4,get(get(a4,'title'),'string'));
close(f1); close(f2); close(f3); close(f4);

    Input Arguments

    expand all

    y — Response variable. Vector.

    Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    X — Predictor variables. Matrix.

    Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.

    Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'alpha',0.01 , 'R2th',0.99 , 'fullreweight',true , 'plotsPI',1

    alpha —test size.scalar.

    Number between 0 and 1 which defines test size to declare the outliers. The default value is 0.01.

    Example: 'alpha',0.01

    Data Types: double

    R2th —R2 threshold.scalar.

    Scalar which defines the value R2 does have to exceed. For example if R2 based on good observations is 0.92 and R2th is 0.90 the estimate of the variance of the residuals which is used to declare the outliers is adjusted in order to have a value of R2 which is equal to 0.90. A similar correction is applied to compute the prediction intervals. The default value of R2th is 1 which means that there is no correction.

    Example: 'R2th',0.99

    Data Types: double

    fullreweight —Option to declare outliers.boolean.

    If fullreweight is true (default option), the list of outliers refers to all the units whose residuals is above the threshold else if it is false the outliers are the observaions which by procedure FSR had been declared outliers and have a residual greater than threshold

    Example: 'fullreweight',true

    Data Types: double

    plotsPI —Plot of prediction intervals.scalar.

    If plotsPI =1 and the number of regressors (excluding the constant term) is equal 1, it is possible to see on the screen the yX scatter with superimposed the prediction intervals using a confidence level 1-alpha, else no plot is shown on the screen

    Example: 'plotsPI',1

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    outliers

    k x 1 vector containing the list of the units declared outliers by procedure FSR or NaN if the sample is homogeneous
    beta

    p-by-1 vector containing the estimated regression parameter by procedure FSR
    outliersr

    k1-by-1 vector containing the list of the units declared outliers after the reweighting step or NaN if the sample is homogeneous
    betar

    p-by-1 vector containing the estimated regression parameter after the reweighting step
    rstud

    n-by-2 matrix.

    First column = studentized residuals;

    Second column = p-values (computed using as reference distribution the Student t)
    class

    'FSRr'.

    varargout —xnew = vector with a number of new points where to evaluate the prediction interval. -by-new is a vector

    ypred = values predicted by the fitted model on xnew. Vector of length(xnew) yci = Confidence intervals. A two-column matrix with each row providing one interval.

    References

    Riani, M., Atkinson, A.C. and Cerioli, A. (2009), Finding an unknown number of multivariate outliers, "Journal of the Royal Statistical Society Series B", Vol. 71, pp. 201-221.

    See Also

    This page has been automatically generated by our routine publishFS