FSR

FSR computes forward search estimator in linear regression

expand all in page

Syntax

Description

example

out =FSR(y, X) FSR with all default options.

example

out =FSR(y, X, Name, Value) FSR with optional arguments.

Examples

expand all

  • FSR with all default options.

    • Run this code to see the output shown in the help file. 

    n=200;
p=3;
randn('state', 123456);
X=randn(n,p);
% Uncontaminated data
y=randn(n,1);
% Contaminated data
ycont=y;
ycont(1:5)=ycont(1:5)+6;
[out]=FSR(ycont,X,'plots',2);

  • FSR with optional arguments.

    • Run this code to see the output shown in the help file. 

    state=100;
randn('state', state);
n=100;
X=randn(n,3);
bet=[3;4;5];
y=3*randn(n,1)+X*bet;
y(1:20)=y(1:20)+13;
[outFS]=FSR(y,X,'plots',2);
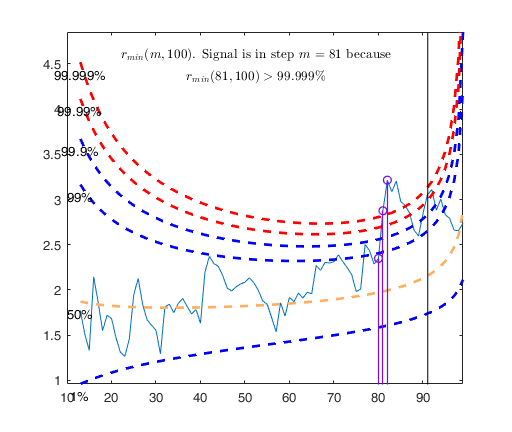
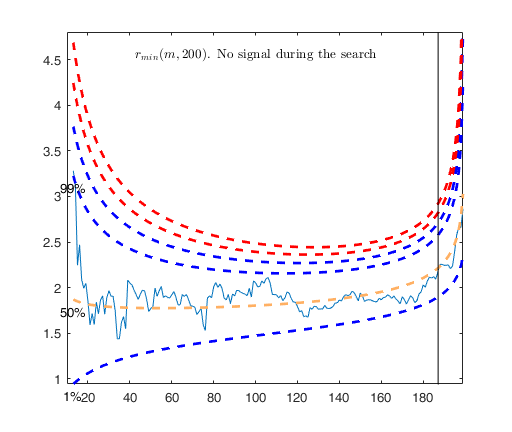
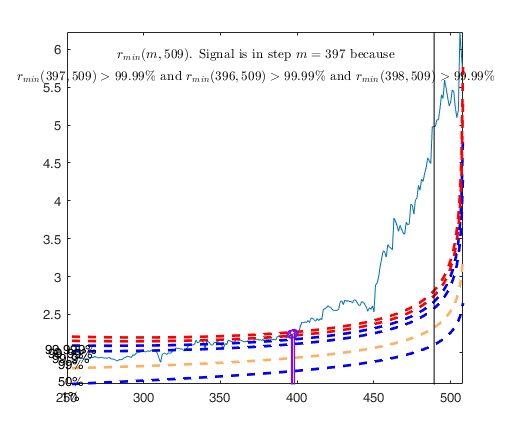
% The envelopes based on all the observations show that in the central
% part of the search the observed curve is well beyond the extreme
% thresholds. More precisely, the message inside the graph informs that
% the signal took place in step 81 because the value of minimum deletion
% residual in this step was greater than 99.999% threshold.
% Once a signal takes place the envelopes are resuperimposed until a
% stopping rule is fulfilled.
% The procedure of resuperimposing envelopes in this case stops when
% n = 85, the first time in which we have a value of rmin(m) for
% $n>=m^\dagger-1$ greater than the 99% threshold. The group can
% therefore be considered as homogeneous up to when we include 84 units.
    Warning: Using 'state' to set RANDN's internal state causes RAND, RANDI, and
RANDN to use legacy random number generators.  This syntax is not recommended.
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace the
old syntax. 
-------------------------
Signal detection loop
Tentative signal in central part of the search: step m=81 because
rmin(81,100)>99.999%

-------------------
Signal validation exceedance of upper envelopes
Validated signal
-------------------------------
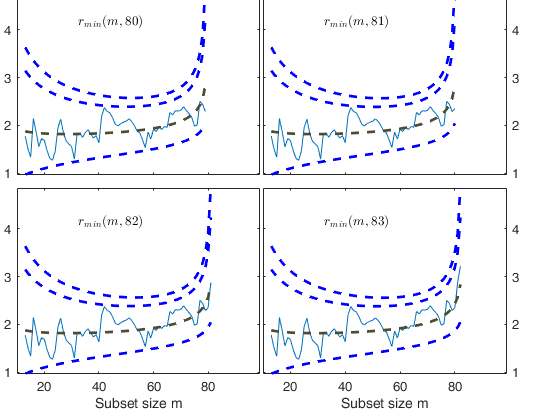
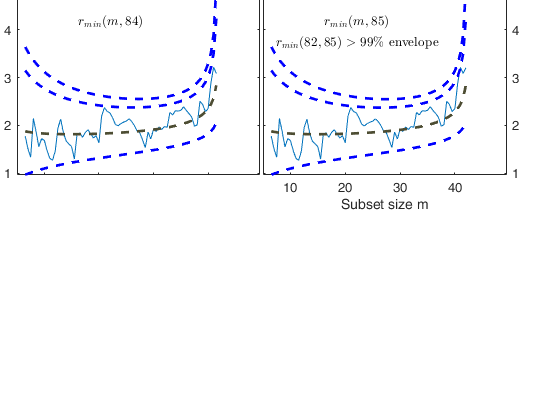
Start resuperimposing envelopes from step m=80
Superimposition stopped because r_{min}(82,85)>99% envelope
$r_{min}(82,85)>99$\% envelope
Subsample of 84 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=16
Summary of the exceedances
           1          99         999        9999       99999
           0          17          10           9           6
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • FSR with optional arguments.

    • Monitor the exceedances from m=60 without showing plots. 

    n=200;
p=3;
X=rand(n,p);
y=rand(n,1);
[out]=FSR(y,X,'init',60,'plots',0);

  • Extract all possible subsamples in order to find subset to initialize the search.

    • n=50;
p=3;
X=randn(n,p);
y=randn(n,1);
[out]=FSR(y,X,'nsamp',0);

  • Example for various combinations of the labeladd, bivarfit and multivarfit options.

    • n=200;
p=3;
X=randn(n,p);
y=randn(n,1);
[out]=FSR(y,X, 'labeladd','1','bivarfit','1','multivarfit','1');
    -------------------------
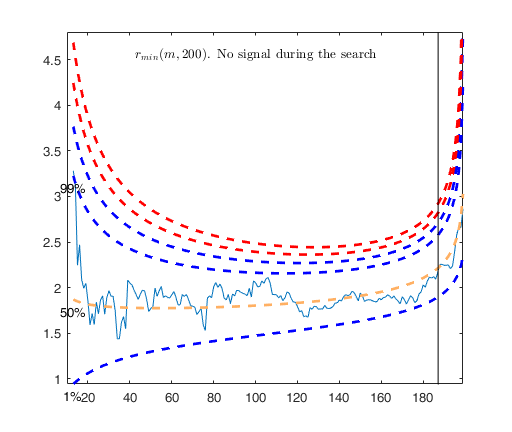
Signal detection loop
Sample seems homogeneous, no outlier has been found
Summary of the exceedances
           1          99         999        9999       99999
           0           1           0           0           0
    Click here for the graphical output of this example (link to Ro.S.A. website)

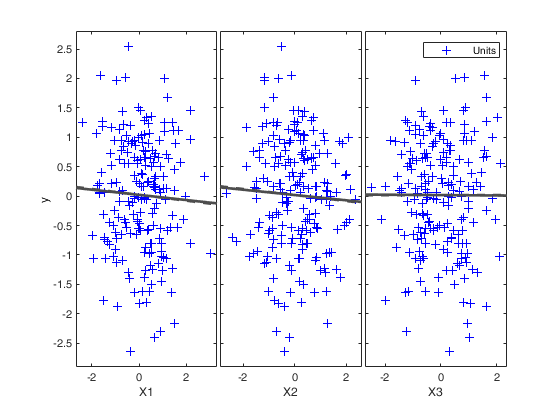
  • Example of use of options xlim and ylim (Hawkins data).

    • load('hawkins.txt','hawkins');
y=hawkins(:,9);
X=hawkins(:,1:8);
% Use of FSR starting with 1000 subsamples
[out]=FSR(y,X,'nsamp',1000);
% Use of FSR starting with 1000 subsamples
% focusing in the output plots to the interval 1-6 on the y axis and
% to steps 30-90.
[out]=FSR(y,X,'nsamp',1000,'ylim',[1 6],'xlim',[30 90]);

  • Example of use of options nameX and nameY with contaminated data.

    • n=200;
p=3;
state1=123498;
randn('state', state1);
X=randn(n,p);
y=randn(n,1);
kk=33;
% shift contamination of the first 33 units of the response
y(1:kk)=y(1:kk)+6;
nameX={'age', 'salary', 'position'};
namey='salary';
[out]=FSR(y,X,'nameX',nameX,'namey',namey);

  • Example of point mass contamination.

    • n=130;
p=5;
state1=123498;
randn('state', state1);
X=randn(n,p);
y=randn(n,1);
kk=30;
% point mass contamination of the first kk units
X(1:kk,:)=1;
y(1:kk)=3;
[out]=FSR(y,X);

  • Example of the use of option threshoutX.

    • In this example a set of remote units is added to a cloud of points. 

    % The purpose of this example is to show that in presence of units very far
% from the bulk of th data (bad or good elverage points) it is necessary to
% bound their effect putting a constraint on their leverage hi=xi'(X'X)xi
rng('default')
rng(10000)
n=100;
p=1;
X=randn(n,p);
epsil=10;
beta=ones(p,1);
y=X*beta+randn(n,1)*epsil;
% Add 10 very remote points
add=3;
Xadd=X(1:add,:)+5000;
yadd=y(1:add)+200;
Xall=[X;Xadd];
yall=[y;yadd];
outNoLevConstr=FSR(yall,Xall,'msg',0,'ylim',[0 5]);
xylim=axis;
ylabel('mdr')
title('FS without bound on the leverage')
% threshoutX is passed as astructure
threshoutX=struct;
threshoutX.threshlevoutX=5;
% Use the instruction below if you wish to change the confidence level to
% be used to find outlierd in the X space
% threshoutX.bonflevoutX=0.99
outWithLevConstr=FSR(yall,Xall,'threshoutX',threshoutX,'msg',0,'ylim',[0 5]);
title('FS with bound on the leverage')

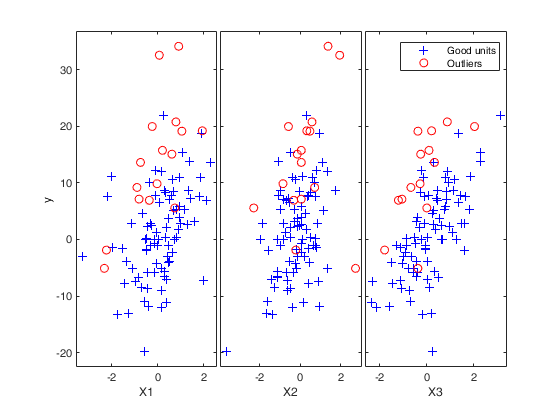
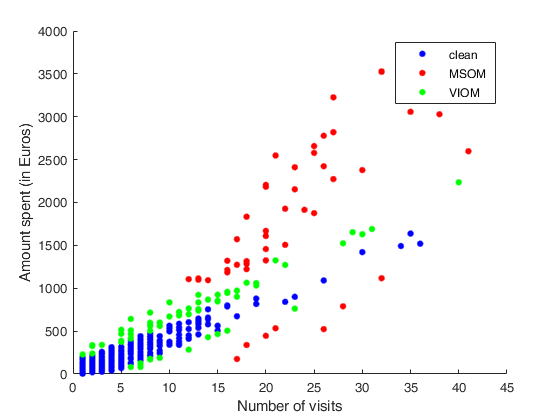
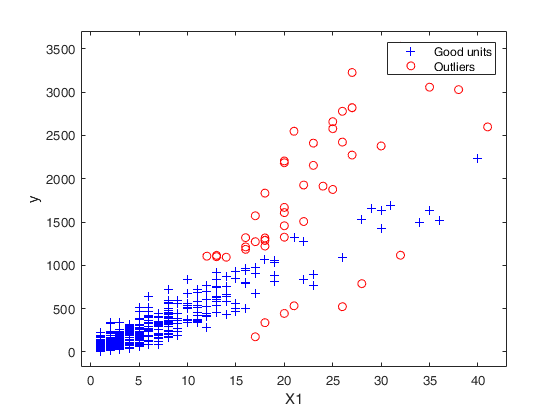
  • Example to detect both VIOM and MSOM outliers using weak=true.

    • loyalty data 

    load('loyalty');
y = loyalty{:,end};
X = loyalty{:,1};
xla = 'Number of visits';
yla = 'Amount spent (in Euros)';
n = size(X,1);
% run FSR to detect a weaker signal indicating VIOM
FSRoutw = FSR(y, X, 'intercept', false, ...
'init', floor(n/2)-1, 'msg', 0, 'plots', 1, 'weak', true);
trim_FSR =  FSRoutw.outliers;
down_FSR =  FSRoutw.VIOMout;
clean_FSR = FSRoutw.ListCl;
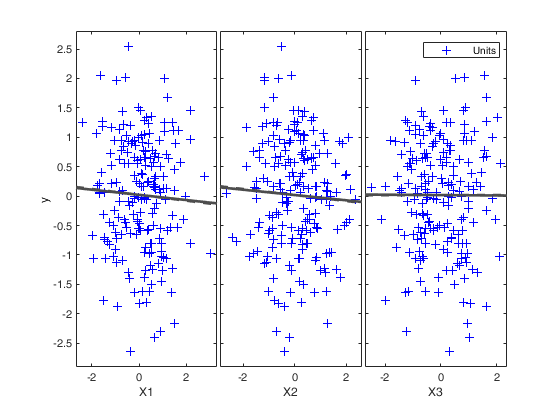
% plotting
figure
plot(X(clean_FSR, :), y(clean_FSR), 'b.', 'MarkerSize', 15, 'DisplayName', 'clean');
hold('on')
plot(X(trim_FSR, :), y(trim_FSR), 'r.', 'MarkerSize', 15, 'DisplayName', 'MSOM');
plot(X(down_FSR, :), y(down_FSR), 'g.', 'MarkerSize', 15, 'DisplayName', 'VIOM');
drawnow
clb = clickableMultiLegend(gca, 'Location', 'northeast');
set(clb,'FontSize',12);
xlabel(xla);
ylabel(yla);
box
cascade
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    y — Response variable. Vector.

    Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    X — Predictor variables. Matrix.

    Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.

    Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'bsbmfullrank',false , 'bonflev',0.99 , 'h',round(n*0,75) , 'init',100 starts monitoring from step m=100 , 'intercept',false , 'lms',1 , 'msg',false , 'nocheck',true , 'nsamp',1000 , 'threshoutX',1 , 'weak',true , 'plots',1 , 'bivarfit','2' , 'labeladd','1' , 'multivarfit','1' , 'nameX',{'NameVar1','NameVar2'} , 'namey','NameOfResponse' , 'tag',{'plmdr' 'plyXplot'}; ,

    bsbmfullrank —Dealing with singular X matrix.boolean.

    This option tells how to behave in case subset at step m (say bsbm) produces a singular X. In other words, this options controls what to do when rank(X(bsbm,:)) is smaller then number of explanatory variables. If bsbmfullrank =true (default) these units (whose number is say mnofullrank) are constrained to enter the search in the final n-mnofullrank steps else the search continues using as estimate of beta at step m the estimate of beta found in the previous step.

    Example: 'bsbmfullrank',false

    Data Types: logical

    bonflev —Signal to use to identify outliers.scalar | empty value (default).

    Option to be used if the distribution of the data is strongly non normal and, thus, the general signal detection rule based on consecutive exceedances cannot be used. In this case bonflev can be: - a scalar smaller than 1 which specifies the confidence level for a signal and a stopping rule based on the comparison of the minimum MD with a Bonferroni bound. For example if bonflev=0.99 the procedure stops when the trajectory exceeds for the first time the 99% bonferroni bound.

    - A scalar value greater than 1. In this case the procedure stops when the residual trajectory exceeds for the first time this value.

    Default value is '', which means to rely on general rules based on consecutive exceedances.

    Example: 'bonflev',0.99

    Data Types: double

    h —The number of observations that have determined the least trimmed squares estimator.scalar.

    h is an integer greater or equal than p but smaller then n. Generally if the purpose is outlier detection h=[0.5*(n+p+1)] (default value). h can be smaller than this threshold if the purpose is to find subgroups of homogeneous observations.

    In this function the LTS/LMS estimator is used just to initialize the search.

    Example: 'h',round(n*0,75)

    Data Types: double

    init —Search initialization.scalar.

    It specifies the initial subset size to start monitoring exceedances of minimum deletion residual, if init is not specified it set equal to: p+1, if the sample size is smaller than 40;

    min(3*p+1,floor(0.5*(n+p+1))), otherwise.

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    lms —Criterion to use to find the initial subset to initialize the search.scalar, vector | structure.

    lms specifies the criterion to use to find the initial subset to initialize the search (LMS, LTS with concentration steps, LTS without concentration steps or subset supplied directly by the user).

    The default value is 1 (Least Median of Squares is computed to initialize the search). On the other hand, if the user wants to initialze the search with LTS with all the default options for concentration steps then lms=2. If the user wants to use LTS without concentration steps, lms can be a scalar different from 1 or 2. If lms is a struct it is possible to control a series of options for concentration steps (for more details see option lms inside LXS.m) LXS.

    If, on the other hand, the user wants to initialize the search with a prespecified set of units there are two possibilities: 1) lms can be a vector with length greater than 1 which contains the list of units forming the initial subset. For example, if the user wants to initialize the search with units 4, 6 and 10 then lms=[4 6 10];

    2) lms is a struct which contains a field named bsb which contains the list of units to initialize the search. For example, in the case of simple regression through the origin with just one explanatory variable, if the user wants to initialize the search with unit 3 then lms=struct;

    Value Description
    bsb

    3;

    Example: 'lms',1

    Data Types: double

    msg —Level of output to display.boolean.

    It controls whether to display or not messages on the screen If msg==true (default) messages are displayed on the screen about step in which signal took place else no message is displayed on the screen.

    Example: 'msg',false

    Data Types: logical

    nocheck —Check input arguments.boolean.

    If nocheck is equal to true no check is performed on matrix y and matrix X.

    Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.

    Example: 'nocheck',true

    Data Types: double

    nsamp —Number of subsamples which will be extracted to find the robust estimator.scalar.

    If nsamp=0 all subsets will be extracted.

    They will be (n choose p).

    If the number of all possible subset is <1000 the default is to extract all subsets otherwise just 1000.

    Example: 'nsamp',1000

    Data Types: double

    threshoutX —threshold to bound the effect of high leverage units.empty value (default) | scalar equal to 1 | structure.

    If the design matrix X contains several high leverage units (that is units which are very far from the bulk of the data), it may happen that the best subset of LXS may include some of these units, or it may happen that these units have a deletion residual which is very small due to their extremely high value of $h_i$. bonflevoutX=1 imposes the constraints that: 1) the extracted subsets which contain at least one unit declared as outlier in the X space by FSM using a Bonferronized confidence level of 0.99 are removed from the list of candidate subsets to find the LXS solution.

    2) imposes the contrainst that $h_i(m^*)$ cannot exceed $10 \times p/m$.

    If threshoutX is a structure, it contains the following fields:

    Value Description
    bonflevoutX

    specifies the Bonferronized confidence level to be used to find the outliers in the X space. If this field is not present a 99 per cent confidence level is used.
    threshlevoutX

    specifies the threshold to bound the effect of high leverage units in the computation of deletion residuals. In the computation of the quantity $h_i(m^*) = x_i^T\{X(m^*)^TX(m^*)\}^{-1}x_i$, $i \notin S^{(m)}_*$, units which very far from the bulk of the data (represented by $X(m^*)$) will have a huge value of $h_i(m^*)$ and consequently of the deletion residuals.

    In order to tackle this problem it is possible to put a bound to the value of $h_i(m^*)$. For example threshoutX.threshlevoutX=r imposes the contrainst that $h_i(m^*)$ cannot exceed $r \times p/m$. If this field is not present the default threshold of 10 is imposed.

    Example: 'threshoutX',1

    Data Types: double

    weak —Indicator to use a different decision rule to detect the signal and flag outliers.false (default) | true.

    If weak=false default FSRcore values are used, if weak=true 'stronger' quantiles are used as a decision rule to trim outliers and VIOM outliers are the ones entering the Search after the first signal.

    Example: 'weak',true

    Data Types: logical

    plots —Plot on the screen.scalar.

    If plots=1 (default) the plot of minimum deletion residual with envelopes based on n observations and the yXplot matrix with the outliers highlighted is produced.

    If plots=2 the user can also monitor the intermediate plots based on envelope superimposition.

    Else no plot is produced.

    Example: 'plots',1

    Data Types: double

    bivarfit —Superimpose bivariate least square lines.character.

    This option adds one or more least squares lines, based on SIMPLE REGRESSION of y on Xi, to the plots of y|Xi.

    bivarfit = '' is the default: no line is fitted.

    bivarfit = '1' fits a single ols line to all points of each bivariate plot in the scatter matrix y|X.

    bivarfit = '2' fits two ols lines: one to all points and another to the group of the genuine observations. The group of the potential outliers is not fitted.

    bivarfit = '0' fits one ols line to each group. This is useful for the purpose of fitting mixtures of regression lines.

    bivarfit = 'i1' or 'i2' or 'i3' etc. fits an ols line to a specific group, the one with index 'i' equal to 1, 2, 3 etc. Again, useful in case of mixtures.

    Example: 'bivarfit','2'

    Data Types: char

    labeladd —Add outlier labels in plot.character.

    If this option is '1', we label the outliers with the unit row index in matrices X and y. The default value is labeladd='', i.e. no label is added.

    Example: 'labeladd','1'

    Data Types: char

    multivarfit —Superimpose multivariate least square lines.character.

    This option adds one or more least square lines, based on MULTIVARIATE REGRESSION of y on X, to the plots of y|Xi.

    multivarfit = '' is the default: no line is fitted.

    multivarfit = '1' fits a single ols line to all points of each bivariate plot in the scatter matrix y|X. The line added to the scatter plot y|Xi is avconst + Ci*Xi, where Ci is the coefficient of Xi in the multivariate regression and avconst is the effect of all the other explanatory variables different from Xi evaluated at their centroid (that is overline{y}'C)) multivarfit = '2' equal to multivarfit ='1' but this time we also add the line based on the group of unselected observations (i.e. the normal units).

    Example: 'multivarfit','1'

    Data Types: char

    nameX —Add variable labels in plot.cell array of strings.

    Cell array of strings of length p containing the labels of the variables of the regression dataset. If it is empty (default) the sequence X1, ..., Xp will be created automatically

    Example: 'nameX',{'NameVar1','NameVar2'}

    Data Types: cell

    namey —Add response label.character.

    String containing the label of the response

    Example: 'namey','NameOfResponse'

    Data Types: char

    tag —tags to the plots which are created.character | cell array of characters.

    This option enables to add a tag to the plots which are created. The default tag names are: fsr_mdrplot for the plot of mdr based on all the observations;

    fsr_yXplot for the plot of y against each column of X with the outliers highlighted;

    fsr_resuperplot for the plot of resuperimposed envelopes. The first plot with 4 panel of resuperimposed envelopes has tag fsr_resuperplot1, the second fsr_resuperplot2 ...

    If tag is character or a cell of characters of length 1, it is possible to specify the tag for the plot of mdr based on all the observations;

    If tag is a cell of length 2 it is possible to control both the tag for the plot of mdr based on all the observations and the tag for the yXplot with outliers highlighted.

    If tag is a cell of length 3 the third element specifies the names of the plots of resuperimposed envelopes.

    Example: 'tag',{'plmdr' 'plyXplot'};

    Data Types: char or cell

    xlim —Control x scale in plot.vector.

    Vector with two elements minimum and maximum on the x axis. Default value is '' (automatic scale)

    Example: 'xlim',[0,10] sets the minimum value to 0 and the max to 10 on the x axis

    Data Types: double

    ylim —Control y scale in plot.vector.

    Vector with two elements controlling minimum and maximum on the y axis.

    Default value is '' (automatic scale)

    Example: 'ylim',[0,10] sets the minimum value to 0 and the max to 10 on the y axis

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    ListOut

    row vector containing the list of the units declared as outliers or NaN if the sample is homogeneous. If
    outliers

    out.ListOut. This field is added for homogeneity with the other robust estimators and is equal to out.ListOut.
    beta

    p-by-1 vector containing the estimated regression parameters (in step n-k).
    scale

    scalar containing the estimate of the scale (sigma).
    residuals

    n x 1 vector containing the estimates of the robust scaled residuals.
    fittedvalues

    n x 1 vector containing the fitted values.
    mdr

    (n-init) x 2 matrix 1st col = fwd search index 2nd col = value of minimum deletion residual in each step of the fwd search
    Un

    (n-init) x 11 matrix which contains the unit(s) included in the subset at each step of the fwd search.

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one.

    Un(1,2) for example contains the unit included in step init+1.

    Un(end,2) contains the units included in the final step of the search.
    nout

    2 x 5 matrix containing the number of times mdr went out of particular quantiles.

    First row contains quantiles 1 99 99.9 99.99 99.999.

    Second row contains the frequency distribution.
    class

    'FSR'.
    VIOMout

    m x 1 vector containing the list of the units declared as VIOM outliers or NaN if they are not present.

    This field is present only if weak = true.
    ListCl

    (n-m) x 1 vector of non-outlying units.

    This field is present only if weak = true.

    References

    Riani, M., Atkinson, A.C. and Cerioli, A. (2009), Finding an unknown number of multivariate outliers, "Journal of the Royal Statistical Society Series B", Vol. 71, pp. 201-221.

    See Also

    |

    This page has been automatically generated by our routine publishFS