LXS
LXS computes the Least Median of Squares (LMS) or Least Trimmed Squares (LTS) estimators
Description
Examples
LXS with default input and output.
Compute LMS estimator without reweighting, add intercept to matrix X and do not produce plots.
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X);
LXS with optional arguments.
Compute LMS estimator, reweight and plot the residuals.
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'rew',1,'plots',1);
LXS with optional output.
Generating the C matrix containing the indices of the subsamples extracted for computing the estimate (the so called elemental sets).
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out,C]=LXS(y,X);
Related Examples
Reweighted LTS estimator.
Compute reweighted LTS estimator and produce the plot of residuals.
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'rew',1,'lms',0,'plots',1);
Specifying the number of subsamples.
Compute LMS estimator, without plots using 20000 subsamples.
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'nsamp',20000);
Specifying a confidence level.
Compute reweighted LMS and use a confidence level for outlier detection equal to 0.999.
rng('default')
n=200;
p=3;
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'rew',1,'conflev',0.999);
Using fast options.
Compute LTS using fast options detection equal to 0.999.
lms=struct;
% Do 5 refining steps for each elemental subset
lms.refsteps=5;
% Store the best 10 subsets
lms.bestr=10;
n=200;
p=3;
rng('default');
rng(123456)
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'lms',lms,'plots',1);
 We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
 We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
close all;
rng('default');
rng(100)
n=100;
X=randn(n,3);
bet=[3;4;5];
y=3*randn(n,1)+X*bet;
y(1:20)=y(1:20)+13;
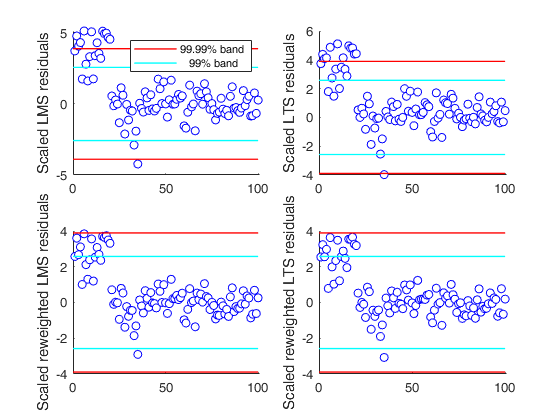
% Define nominal confidence level
conflev=[0.99,1-0.01/length(y)];
% Define number of subsets
nsamp=3000;
% Define the main title of the plots
titl='';
% LMS with no reweighting
[outLMS]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1));
h=subplot(2,2,1);
laby='Scaled LMS residuals';
resindexplot(outLMS.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev)
% LTS with no reweighting
h=subplot(2,2,2);
[outLTS]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'lms',0);
laby='Scaled LTS residuals';
resindexplot(outLTS.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev);
% LMS with reweighting
[outLMSr]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'rew',1);
h=subplot(2,2,3);
laby='Scaled reweighted LMS residuals';
resindexplot(outLMSr.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev)
% LTS with reweighting
[outLTSr]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'rew',1,'lms',0);
h=subplot(2,2,4);
laby='Scaled reweighted LTS residuals';
resindexplot(outLTSr.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev);
% By simply changing the seed to 543 (state=543), using a Bonferroni size of 1%, no unit is declared as outlier.Total estimated time to complete LMS: 0.01 seconds Total estimated time to complete LTS: 0.01 seconds Total estimated time to complete LMS: 0.03 seconds Total estimated time to complete LTS: 0.04 seconds
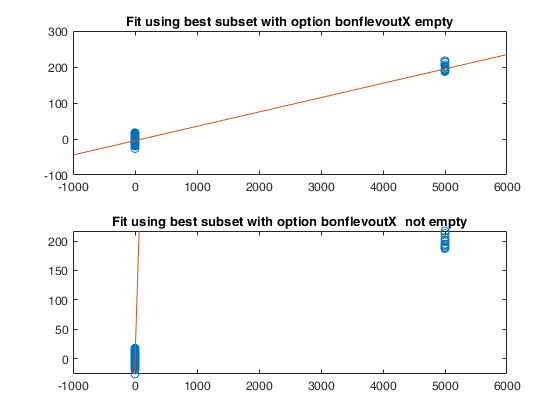
 Example of the use of option bonflevoutX.
Example of the use of option bonflevoutX.
 Example of the use of option bonflevoutX.
Example of the use of option bonflevoutX.In this example, a set of remote units is added to a cloud of points.
% The purpose of this example is to show that while best LMS using all
% default options contains some of the remote units. In order to make sure
% that the remote units are excluded from the best LMS subset it is
% necessary to use option bonflevoutX.
rng('default')
rng(10000)
n=100;
p=1;
X=randn(n,p);
epsil=10;
beta=ones(p,1);
y=X*beta+randn(n,1)*epsil;
% Add 10 very remote points
add=10;
Xadd=X(1:add,:)+5000;
yadd=y(1:add)+200;
Xall=[X;Xadd];
yall=[y;yadd];
out=LXS(yall,Xall);
subplot(2,1,1)
plot(Xall,yall,'o')
xylim=axis;
line(xylim(1:2),out.beta(1)+out.beta(2)*xylim(1:2))
title('Fit using best subset with option bonflevoutX empty')
subplot(2,1,2);
plot(Xall,yall,'o')
out=LXS(yall,Xall,'bonflevoutX',0.99);
line(xylim(1:2),out.beta(1)+out.beta(2)*xylim(1:2))
ylim(xylim(3:4));
title('Fit using best subset with option bonflevoutX not empty')Total estimated time to complete LMS: 0.01 seconds Total estimated time to complete LMS: 0.06 seconds ------------------------------ Warning: Number of subsets without full rank or excluded because containing remote units in the X space equal to 17.1 %
LXS with optional arguments.
Compute LTS estimator, reweight and plot the residuals.
% Use a confidence level for reweighting using 0.99 and a simultaneous
% confidence interval for outlier detection
n=200;
p=3;
rng('default')
rng(123456);
X=randn(n,p);
y=randn(n,1);
y(1:5)=y(1:5)+6;
[out]=LXS(y,X,'rew',1,'conflev',1-0.01/n,'conflevrew',0.99,'plots',1);Input Arguments
y — Response variable.
Vector.
A vector with n elements that contains the response variable.
It can be either a row or a column vector.
Data Types: single| double
X — Predictor variables.
Matrix.
Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'bdp',0.4
, 'bonflevoutX',0.95
, 'conflev',0.99
, 'conflevrew',0.99
, 'h',round(n*0,75)
, 'intercept',false
, 'lms',1
, 'nocheck',true
, 'nomes',true
, 'msg',false
, 'nsamp',0
, 'rew',true
, 'SmallSampleCor',3
, 'yxsave',1
, 'plots',1
bdp
—breakdown point.scalar.
It measures the fraction of outliers the algorithm should resist.
In this case any value greater than 0, but smaller or equal than 0.5, will do fine. If, on the other hand, the purpose is subgroups detection, then bdp can be greater than 0.5. In any case, however, n*(1-bdp) must be greater than p. If this condition is not fulfilled an error will be given. Please specify h or bdp not both.
Example: 'bdp',0.4
Data Types: double
bonflevoutX
—remote units in the X space.scalar | empty (default).
If the design matrix X contains several high leverage units (that is, units which are very far from the bulk of the data), it may happen that the best subset may include some of these units.
If bonflevoutX is not empty, outlier detection procedure FSM is applied to the design matrix X, using name/pair option 'bonflev',bonflevoutX. The extracted subsets, which contain at least one unit declared as outlier in the X space by FSM, are removed (more precisely they are treated as singular subsets) from the list of candidate subsets to find the LXS solution. The default value of bonflevoutX is empty, that is FSM is not invoked.
Example: 'bonflevoutX',0.95
Data Types: double
conflev
—Confidence level which is
used to declare units as outliers.scalar Usually conflev=0.
95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).
Default value is 0.975
Example: 'conflev',0.99
Data Types: double
conflevrew
—Confidence level used for reweighting.scalar.
Number between 0 and 1 containing confidence level which is used to do the reweighting step. Default value is the one specified in previous option conflev.
Example: 'conflevrew',0.99
Data Types: double
h
—The number of observations that have determined the least
trimmed squares estimator.scalar.
The number of observations that have determined the least trimmed squares estimator. h is an integer greater than p (number of columns of matrix X including the intercept, but smaller then n. If the purpose is outlier detection, then h does not have to be smaller than [0.5*(n+p+1)] (default value). On the other hand, if the purpose is to find subgroups of homogeneous observations, h can be smaller than [0.5*(n+p+1)]. If h <p+1 an error will be given.
Example: 'h',round(n*0,75)
Data Types: double
intercept
—Indicator for constant term.true (default) | false.
Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.
Example: 'intercept',false
Data Types: boolean
lms
—Estimation method.scalar, vector | structure.
If lms is a scalar = 1 (default) Least Median of Squares is computed, else if lms is a scalar = 2 fast lts with the all default options is used else if lms is a scalar different from 1 and 2 standard lts is used (without concentration steps) else if lms is a struct fast lts (with concentration steps) is used.
In this case, the user can control the following options: lms.refsteps : scalar defining number of refining iterations in each subsample (default = 3). refsteps = 0 means "raw-subsampling" without iterations.
lms.reftol : scalar. Default value of tolerance for the refining steps The default value is 1e-6.
lms.bestr : scalar defining number of "best betas" to remember from the subsamples. These will be later iterated until convergence (default=5).
lms.refstepsbestr : scalar defining number of refining iterations for each best subset (default = 50).
lms.reftolbestr : scalar. Default value of tolerance for the refining steps for each of the best subsets.
The default value is 1e-8.
Example: 'lms',1
Data Types: double
nocheck
—Check input arguments.boolean.
If nocheck is equal to true, no check is performed on matrix y and matrix X. Notice that when no check is true y and X are left unchanged, that is the additional column of ones for the intercept is not added. As default nocheck=false. The controls on h, bdp and nsamp still remain.
Example: 'nocheck',true
Data Types: boolean
nomes
—It controls whether to display or not on the screen
messages about estimated time to compute LMS (LTS) .boolean.
If nomes is equal to true, no message about estimated time to compute LMS (LTS) is displayed, else if nomes is equal to false (default), a message about estimated time is displayed.
Example: 'nomes',true
Data Types: logical
msg
—It controls whether to display or not messages on the screen.boolean.
If msg==true (default), messages are displayed on the screen about estimated time to compute the estimator and the warnings about 'MATLAB:rankDeficientMatrix', 'MATLAB:singularMatrix' and 'MATLAB:nearlySingularMatrix' are set to off, else no message is displayed on the screen.
Example: 'msg',false
Data Types: logical
nsamp
—Number of subsamples which will be extracted to find the
robust estimator or matrix with pre-extracted subsamples.scalar | matrix.
If nsamp=0, all subsets will be extracted. They will be (n choose p). If nsamp is (say) 200, 200 subsets will be extracted. If nsamp is a matrix of size r-by-p, it contains in the rows the subsets that still have to be extracted.
For example, if p=3 and nsamp=[ 2 4 9; 23 45 49; 90 34 1];
the first subset is made up of units [2 4 9], the second subset of units [23 45 49] and the third subset of units [90 34 1];
Remark: if the number of all possible subset is <1000 the default is to extract all subsets, otherwise just 1000 if fastLTS is used (lms=2 or lms is a structure) or 3000 for standard LTS or LMS.
Example: 'nsamp',0
Data Types: double
rew
—LXS reweighted.boolean.
If rew=true the reweighted version of LTS (LMS) is used and the output quantities refer to the reweighted version, else no reweighting is performed (default).
Example: 'rew',true
Data Types: logical
SmallSampleCor
—Small sample correction factor to control empirical size of
the test.scalar equal to 0 (default) | 1 | 2 | 3 | 4.
- If SmallSampleCor=0 (default) no small sample correction;
- If SmallSampleCor=1 in the reweighting step the nominal threshold based on $\chi^2_{0.99}$ is multiplied by the small sample correction factor, which guarantees that the empirical size of the test is equal to the nominal size;
- If SmallSampleCor =2 Gervini and Yohai procedure is called with 'iterating' false and 'alpha' 0.99 is invoked, that is: weights=GYfilt(stdres,'iterating',false,'alpha',0.99);
- If SmallSampleCor =3 Gervini and Yohai procedure is called with 'iterating' true and 'alpha' 0.99 is invoked, that is: weights=GYfilt(stdres,'iterating',true,'alpha',0.99);
- If SmallSampleCor =4 $\chi^2_{0.99}$ threshold is used that is: weights = abs(stdres)<=sqrt(chi2inv(0.99,1));
Example: 'SmallSampleCor',3
Data Types: double
yxsave
—the response vector y and data matrix X are saved into the output
structure out.scalar.
Default is 0, i.e. no saving is done.
Example: 'yxsave',1
Data Types: double
plots
—Plot on the screen.scalar | structure.
If plots = 1, a plot which shows the robust residuals against index number is shown on the screen. The confidence level which is used to draw the horizontal lines associated with the bands for the residuals is as specified in input option conflev. If conflev is missing, a nominal 0.975 confidence interval will be used.
Example: 'plots',1
Data Types: double
Output Arguments
out — description
Structure
A structure containing the following fields
| Value | Description |
|---|---|
rew |
boolean. if out.rew=true, all subsequent output refers to reweighted, else no reweighting is done. |
beta |
Vector of beta LTS (LMS) coefficient estimates, including the intercept when options.intercept=true. out.beta=[intercept slopes]. |
bs |
p x 1 vector containing the units forming subset associated with bLMS (bLTS). |
residuals |
Vector containing the standardized residuals from the regression. |
scale |
Scale estimate of the residuals. |
weights |
Vector like y containing weights. The elements of this vector are 0 or 1. These weights identify the h observations which are used to compute the final LTS (LMS) estimate. sum(out.weights)=h if there is not a perfect fit otherwise sum(out.weights) can be greater than h. |
h |
The number of observations that have determined the LTS (LMS) estimator, i.e. the value of h. |
outliers |
row vector containing the list of the units declared as outliers using confidence level specified in input scalar conflev. |
conflev |
confidence level which is used to declare outliers. Remark: scalar out.conflev will be used to draw the horizontal lines (confidence bands) in the plots. |
singsub |
Number of subsets without full rank. Notice that if this number is greater than 0.1*(number of subsamples), a warning is produced on the screen. |
class |
'LTS' or 'LMS'. |
y |
response vector Y. The field is present only if option yxsave is set to 1. |
X |
data matrix X. The field is present only if option yxsave is set to 1. |
varargout —C : Indexes of the extracted subsamples.
Matrix
Matrix containing the indexes of the subsamples extracted for computing the estimate (the so called elemental sets). For example, if C(3,:)=[2 5 20], implies that the third extracted subsample is formed by units 2, 5 and 20.
References
Rousseeuw P.J., Leroy A.M. (1987), "Robust regression and outlier detection", Wiley.