A vector with n elements that
contains the response variable.
It can be either a row or a column vector.
Data Types: single| double
Data matrix of explanatory
variables (also called 'regressors')
of dimension (n x p-1). Rows of X represent observations, and
columns represent variables.
Data Types: single| double
Vector containing the
list of units flagged as possible VIOM
outliers to be downweighted.
Example - 'dw',10:15
Data Types: single| double
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
Example:
'intercept',false
, 'mult',false
, 'trim',[1,2,3]
, 'trsh',5
, 'cook',1
If true, a model with constant term will be fitted,
else no constant term will be included.
true (default) | false.
Example: 'intercept',false
Data Types: boolean
If mult==true, the weights are jointly estimated by iterative REML.
Default is mult==false and singularly optimal weights are
estimated using REML closed form solution.
Example: 'mult',false
Data Types: boolean
Vector
that contains the units (row numbers) that are forced to
have 0 weights. By default no units are trimmed, i.e. trim==[].
Example: 'trim',[1,2,3]
Data Types: double
If trsh>0, all the (standard) residuals greater than trsh
are set to 0. [[TBA:modify to studentized or scaled residuals]]
If trsh<1, all the estimated weights smaller than trsh are
forced to be 0.
If trsh==0 (default option), no weights are forced to be 0.
(Note: It might be useful to reduce the computational burden).
Example: 'trsh',5
Data Types: double
Scalar. Default cook==0 and Thompson (1985) formula
based on REMLE is used.
Example: 'cook',1
Data Types: double
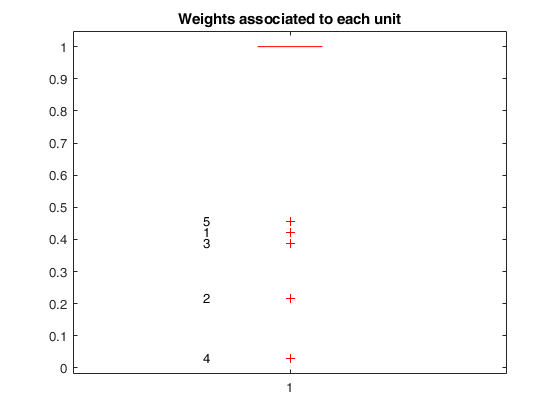
 VIOM with default input.
VIOM with default input.