forecastH

forecastH produce forecasts with confidence bands for regression model with heteroskedasticity

expand all in page

Syntax

  • outFORE=forecastH(y,X,Z)example
  • outFORE=forecastH(y,X,Z,Name,Value)example

Description

example

outFORE =forecastH(y, X, Z) forecastH with all default options.

example

outFORE =forecastH(y, X, Z, Name, Value) Example of use of option bsb.

Examples

expand all

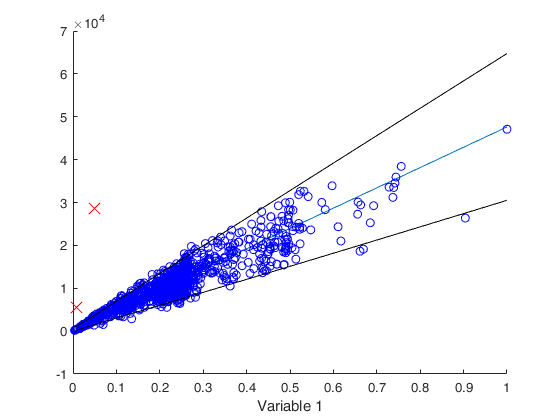
  • forecastH with all default options.

    • close all
load tradeH.mat
y=tradeH{:,2};
X=tradeH{:,1};
X=X./max(X);
Z=log(X);
fore=forecastH(y,X,Z)

  • Example of use of option bsb.

    • close all
load tradeH.mat
y=tradeH{:,2};
X=tradeH{:,1};
X=X./max(X);
Z=log(X);
n=length(y);
bsb=1:n;
% outl = the outliers
outl=[225   660];
bsb(outl)=[];
% call of forecastH with option bsb
outFORE=forecastH(y,X,Z,'bsb',bsb);
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    expand all

  • Example of use of option typeH.

    • close all
load tradeH.mat
y=tradeH{:,2};
X=tradeH{:,1};
X=X./max(X);
Z=log(X);
% Use Harvery's parametrization
fore=forecastH(y,X,Z,'typeH','har');
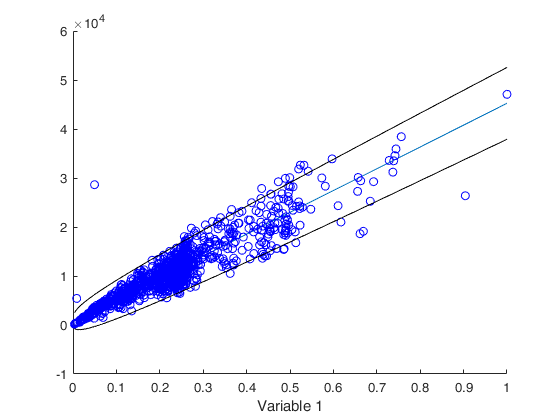
    Click here for the graphical output of this example (link to Ro.S.A. website)

  • Example of use of option outH.

    • close all
load tradeH.mat
y=tradeH{:,2};
X=tradeH{:,1};
X=X./max(X);
Z=log(X);
outEDA=FSRHeda(y,X,Z,0,'init',round(length(y)/2));
% use the output of outEDA
fore=forecastH(y,X,Z,'outH',outEDA);

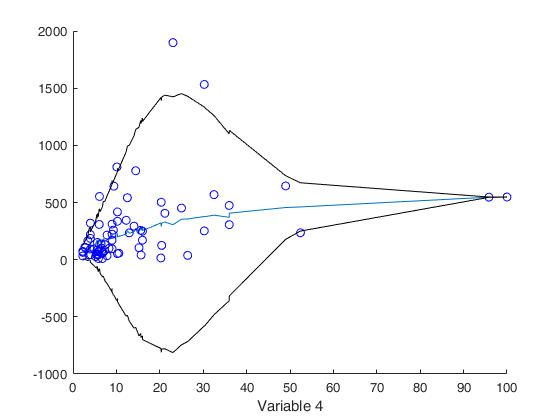
  • Monthly credit card expenditure for 100 individuals.

    • Example of use of option selcolX 

    load('TableF91_Greene');
data=TableF91_Greene{:,:};
n=size(data,1);
% Linear regression of monthly expenditure on a constant, age, income
% its square and a dummy variable for home ownership using the 72
% observations for which expenditure was nonzero produces the residuals
% plotted below
X=zeros(n,4);
X(:,1)=data(:,3);%age
X(:,2)=data(:,6);% Own rent (dummy variable)
X(:,3)=data(:,4);% Income
X(:,4)=(data(:,4)).^2; %Income  square
y=data(:,5); % Monthly expenditure
% Select the 72 observations for which expenditure was nonzero
sel=y>0;
X=X(sel,:);
y=y(sel);
close all
disp('Multiplicative Heteroskedasticity Model')
% Plot of forecasts against column 4
warning('off')
out=forecastH(y,X,[3 4],'typeH','har','selcolX',4);     
warning('on')
    Multiplicative Heteroskedasticity Model
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    y — Response variable. Vector.

    Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    X — Predictor variables in the regression equation. Matrix.

    Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept. Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single| double

    Z — Predictor variables in the skedastic equation. Matrix.

    n x r matrix or vector of length r. If Z is a n x r matrix it contains the r variables which form the scedastic function.

    If Z is a vector of length r it contains the indexes of the columns of matrix X which form the scedastic function.

    Therefore, if for example the explanatory variables responsible for heteroscedasticity are columns 3 and 5 of matrix X, it is possible to use both the syntax regressH(y,X,X(:,[3 5])) or the syntax regressH(y,X,[3 5])

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'bsb',20:50 , 'conflev',0.999 , 'intercept',false , out=regress(y,X,Z); 'outH',out , 'originalScale',false , 'selcolX',2 , 'typeH','har'

    bsb —list of units forming the initial subset.vector | [].

    If bsb=[] (default) then all units are used to produce parameter estimates, else, just the units forming bsb are used

    Example: 'bsb',20:50

    Data Types: double

    conflev —confidence level for the confidence bands.scalar.

    A number between 0 and 1 which defines the confidence level which is used to produce the bands. The default value of conflev is 0.99.

    Example: 'conflev',0.999

    Data Types: double

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    outH —output from fitted heteroskedatic model.struct.

    it is possible to supply the output produced by functions, regressH or regressHart or regressHhar or FSRHeda.

    Note that if input optional argument outH is supplied the model is not fitted and the parameter estimates are taken from outH.

    Example: out=regress(y,X,Z); 'outH',out

    Data Types: struct

    originalScale —confidence band in original or transformed scale.boolean.

    If originalScale is true, plot is shown in the original scale (default). If originalScale is false forecasts are shown on the transformed scale.

    Example: 'originalScale',false

    Data Types: boolean

    selcolX —column of matrix X for which confidence band is wanted.integer in the set $1, 2, \ldots, p-1$.

    Scalar which identifies the column of X to put in x axis of the plot. Default value of selcolX is 1.

    Example: 'selcolX',2

    Data Types: double

    typeH —Parametric function to be used in the skedastic equation.character | string.

    If typeH is 'art' (default) than the skedastic function is modelled as follows \[ \sigma^2_i = \sigma^2 (1 + \exp(\gamma_0 + \gamma_1 Z(i,1) + \cdots + \gamma_{r} Z(i,r))) \] on the other hand, if typeH is 'har' then traditional formulation due to Harvey is used as follows \[ \sigma^2_i = \exp(\gamma_0 + \gamma_1 Z(i,1) + \cdots + \gamma_{r} Z(i,r)) =\sigma^2 (\exp(\gamma_1 Z(i,1) + \cdots + \gamma_{r} Z(i,r)) \]

    Remark. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Example: 'typeH','har'

    Data Types: character or string

    Output Arguments

    expand all

    outFORE — description Structure

    Structure which contains the following fields

    Value Description
    conf

    matrix of size nx4 referred to original space.

    1st column = ordered X values;

    2nd column = fitted values;

    3rd column = lower confidence band;

    4th column = upper confidence band.
    confW

    matrix of size nx4 referred to transformed space.

    1st column = ordered X values;

    2nd column = fitted values;

    3rd column = lower confidence band;

    4th column = upper confidence band.

    References

    Greene, W.H. (1987), "Econometric Analysis", Prentice Hall. [5th edition, section 11.7.1 pp. 232-235, 7th edition, section 9.7.1 pp. 280-282]

    Atkinson, A.C., Riani, M. and Torti, F. (2016), Robust methods for heteroskedastic regression, "Computational Statistics and Data Analysis", Vol. 104, pp. 209-222, http://dx.doi.org/10.1016/j.csda.2016.07.002 [ART]

    See Also

    | | |

    This page has been automatically generated by our routine publishFS