forecastTS
Forecast for a time series with trend, time varying seasonal, level shift and irregular component
Description
forecastTS produces forecasts with confidence bands for a time series with trend (up to third order), seasonality (constant or of varying amplitude) with a different number of harmonics, level shift and explanatory variables.
Quadratic trend and constant seasonal.outFORE
=forecastTS(outEST,
Name, Value)
Examples
 Linear time varying seasonal component.
Linear time varying seasonal component.
 Linear time varying seasonal component.
Linear time varying seasonal component.
close all
rng('default')
rng(1)
model=struct;
model.trend=1;
model.seasonal=103;
modelSIM=model;
modelSIM.trendb=[0 0];
modelSIM.seasonalb=40*[0.1 -0.5 0.2 -0.3 0.3 -0.1 0.222];
modelSIM.signal2noiseratio=20;
T=100;
% Simulate
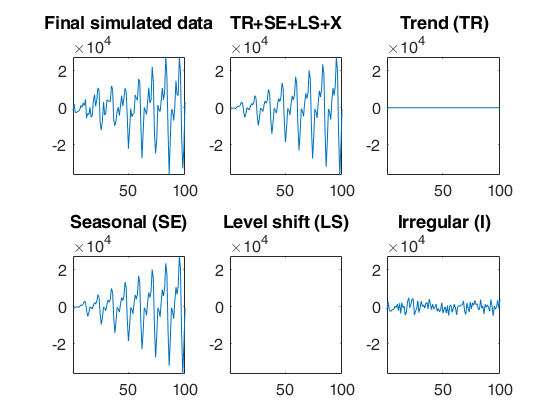
outSIM=simulateTS(T,'model',modelSIM,'plots',1);
ySIM=outSIM.y;
% Estimate
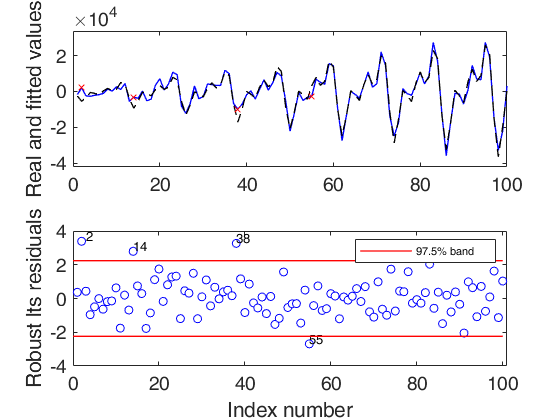
outEST=LTSts(ySIM,'model',model,'plots',1);
% Forecast
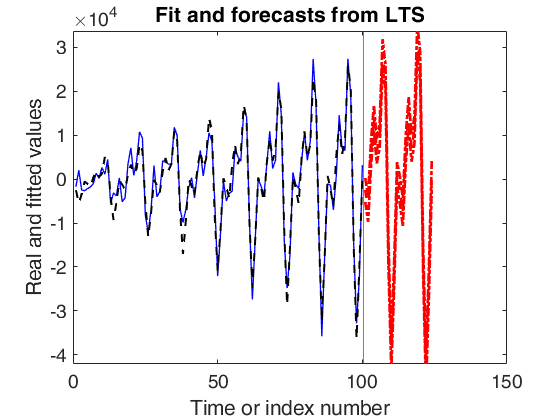
outFORE=forecastTS(outEST,'model',model,'plots',1);
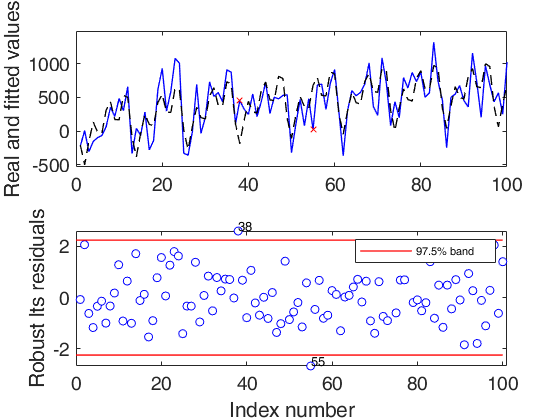
 Quadratic trend and constant seasonal.
Quadratic trend and constant seasonal.
 Quadratic trend and constant seasonal.
Quadratic trend and constant seasonal.
close all
rng(1)
model=struct;
model.trend=2;
model.seasonal=3;
modelSIM=model;
modelSIM.trendb=[100 10 -0.05];
modelSIM.seasonalb=400*[0.1 -0.5 0.2 -0.3 0.3 -0.1];
modelSIM.signal2noiseratio=1;
T=100;
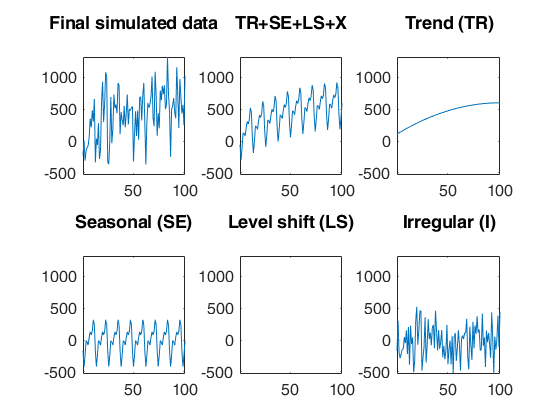
% Simulate
outSIM=simulateTS(T,'model',modelSIM,'plots',1);
ySIM=outSIM.y;
% Estimate
outEST=LTSts(ySIM,'model',model,'plots',1);
% Forecast
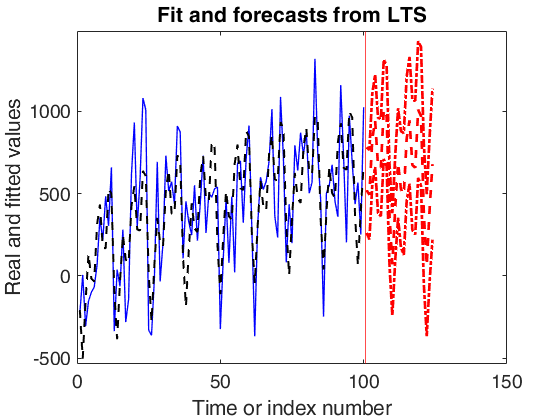
outFORE=forecastTS(outEST,'model',model,'plots',1);
Related Examples
 Simulated time series with quadratic trend, fixed seasonal and level shift.
Simulated time series with quadratic trend, fixed seasonal and level shift.
 Simulated time series with quadratic trend, fixed seasonal and level shift.
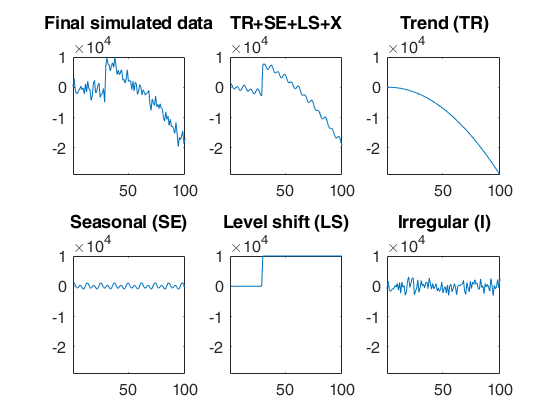
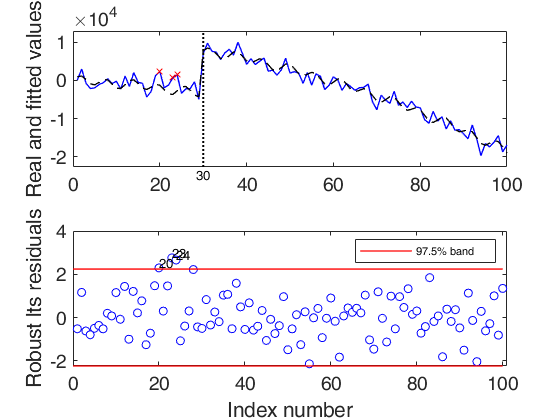
Simulated time series with quadratic trend, fixed seasonal and level shift.A time series of 100 observations is simulated from a model which contains a quadratic trend, a seasonal component with two harmonics no explanatory variables and a level shift in position 30 with size 5000 and a signal to noise ratio equal to 20
close all
rng(1)
model=struct;
model.trend=2;
model.seasonal=2;
model.lshift=30;
modelSIM=model;
modelSIM.trendb=[5,10,-3];
modelSIM.seasonalb=100*[2 4 0.1 8];
modelSIM.signal2noiseratio=20;
modelSIM.lshiftb=10000;
T=100;
% Simulate
outSIM=simulateTS(T,'model',modelSIM,'plots',1);
ySIM=outSIM.y;
% Estimate
% model.lshift=5:T-5 implies that LS is investigated from position
% $5, 6, 7, ..., T-5$,
model.lshift=5:T-5;
outEST=LTSts(ySIM,'model',model,'plots',1,'msg',0);
% Forecast
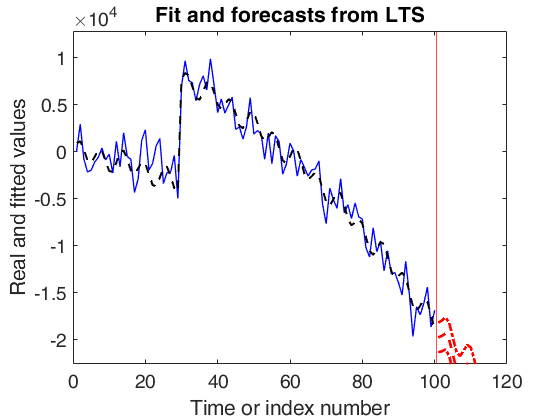
outFORE=forecastTS(outEST,'model',model,'plots',1);
 Contaminated airline data (1).
Contaminated airline data (1).
 Contaminated airline data (1).
Contaminated airline data (1).Load the data.
% 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112 115 145 171 196 204 242 284 315 340 360 417 % Jan
118 126 150 180 196 188 233 277 301 318 342 391 % Feb
132 141 178 193 236 235 267 317 356 362 406 419 % Mar
129 135 163 181 235 227 269 313 348 348 396 461 % Apr
121 125 172 183 229 234 270 318 355 363 420 472 % May
135 149 178 218 243 264 315 374 422 435 472 535 % Jun
148 170 199 230 264 302 364 413 465 491 548 622 % Jul
148 170 199 242 272 293 347 405 467 505 559 606 % Aug
136 158 184 209 237 259 312 355 404 404 463 508 % Sep
119 133 162 191 211 229 274 306 347 359 407 461 % Oct
104 114 146 172 180 203 237 271 305 310 362 390 % Nov
118 140 166 194 201 229 278 306 336 337 405 432 ]; % Dec
y=y(:);
% Contaminate the first 20 observations
y(1:20)=y(1:20)+200;
close all
% Model with linear trend, three harmonics for seasonal component and
% varying amplitude using a linear trend. Search for a level shift
model=struct;
model.trend=1; % linear trend
model.s=12; % monthly time series
model.seasonal=103; % three harmonics with linear time varying seasonality
model.lshift=10:140; % search for level shift
out=LTSts(y,'model',model,'plots',1,'dispresults',true,'msg',0);
% 3 years forecasts
nfore=36;
StartDate=[1949 1];
conflev=0.999; % Wide confidence level for the forecast
outFORE=forecastTS(out,'model',model,'nfore',nfore,'StartDate',StartDate,'conflev',conflev);
Coeff SE t pval
_________ _______ ________ ___________
b_trend1 301.9 3.3707 89.565 1.9432e-121
b_trend2 2.7697 0.03804 72.811 1.2536e-109
b_cos1 -0.94446 2.822 -0.33468 0.73839
b_sin1 -0.46559 1.3917 -0.33454 0.7385
b_cos2 -0.036471 0.11546 -0.31586 0.7526
b_sin2 0.55656 1.6636 0.33455 0.73849
b_cos3 0.22205 0.66425 0.33428 0.73869
b_sin3 -0.093486 0.28116 -0.3325 0.74003
b_varaml 0.58107 1.7666 0.32891 0.74273
b_lshift -225.91 4.5415 -49.743 2.9417e-88
Level shift position t=21
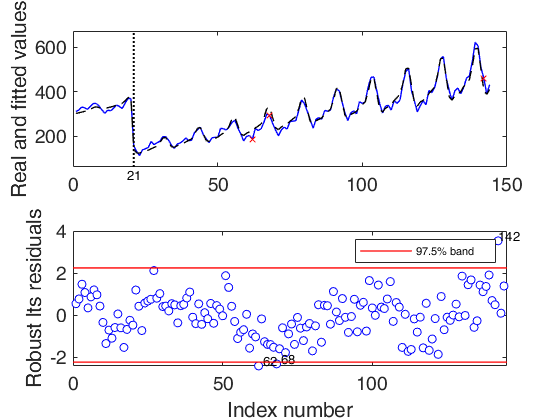
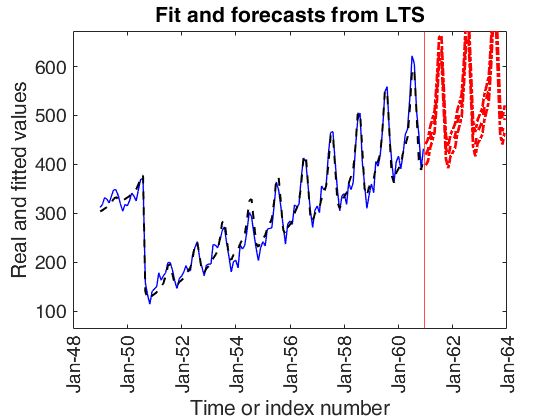
 Contaminated airline data (2).
Contaminated airline data (2).
 Contaminated airline data (2).
Contaminated airline data (2).
close all
% In this example we estimate a model without the seasonal component
% 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112 115 145 171 196 204 242 284 315 340 360 417 % Jan
118 126 150 180 196 188 233 277 301 318 342 391 % Feb
132 141 178 193 236 235 267 317 356 362 406 419 % Mar
129 135 163 181 235 227 269 313 348 348 396 461 % Apr
121 125 172 183 229 234 270 318 355 363 420 472 % May
135 149 178 218 243 264 315 374 422 435 472 535 % Jun
148 170 199 230 264 302 364 413 465 491 548 622 % Jul
148 170 199 242 272 293 347 405 467 505 559 606 % Aug
136 158 184 209 237 259 312 355 404 404 463 508 % Sep
119 133 162 191 211 229 274 306 347 359 407 461 % Oct
104 114 146 172 180 203 237 271 305 310 362 390 % Nov
118 140 166 194 201 229 278 306 336 337 405 432 ]; % Dec
y=y(:);
% Contaminate the first 20 observations
y(1:20)=y(1:20)+200;
% Model with linear trend and no seasonal component. Search for a level shift
model=struct;
model.trend=1; % linear trend
model.s=12; % monthly time series
model.seasonal=0; % no seasonal component
model.lshift=10:(length(y)-10); % search for level shift
out=LTSts(y,'model',model,'plots',1,'dispresults',true,'msg',0);
% 3 years forecasts
nfore=36;
StartDate=[1949 1];
conflev=0.999; % Wide confidence level for the forecast
outFORE=forecastTS(out,'model',model,'nfore',nfore,'StartDate',StartDate,'conflev',conflev);
Coeff SE t pval
_______ ________ _______ __________
b_trend1 307.43 7.2337 42.5 2.8696e-82
b_trend2 2.3919 0.087445 27.354 3.0083e-58
b_lshift -214.71 9.7761 -21.963 2.3563e-47
Level shift position t=21
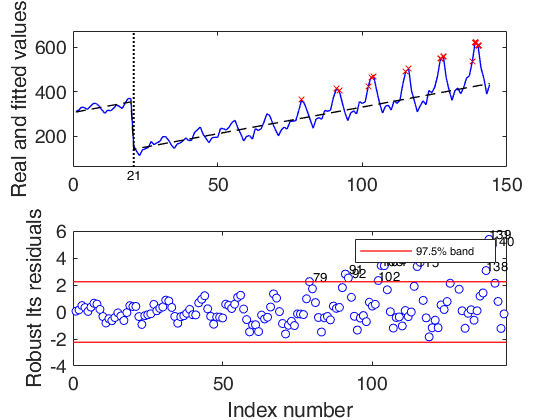
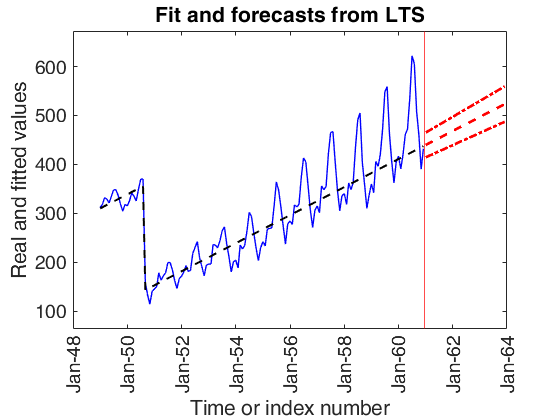
Example with simulated data.
Simulate data with linear trend, time varying seasonal component, and level shift
rng(1)
model=struct;
model.trend=1;
model.trendb=[1 1];
model.seasonal=103;
model.seasonalb=40*[0.5 -0.5 0.3 -0.3 0.1 -0.1 0.222];
model.lshift=40;
model.lshiftb=13000;
model.signal2noiseratio=20;
T=150;
FileNameOutput=[pwd filesep 'ysimout.txt'];
outSIM=simulateTS(T,'model',model,'FileNameOutput',FileNameOutput,...
'plots',true,'samescale',true);
y=outSIM.y;
% Data contamination
y(131:140)=y(131:140)-29000;
% Estimation
modelEST=struct;
modelEST.trend=1;
modelEST.seasonal=103;
modelEST.lshift=30:(length(y)-30);
outEST=LTSts(y,'model',modelEST,'dispresults',true,'plots',0);
% Forecasting
% nfore= number of forecasts;
nfore=36;
% Forecasts with a 99.9 per cent confidence level
OUTfore=forecastTS(outEST,'model',modelEST,'nfore',nfore,'conflev',0.999);
Example of forecasting in a model with explanatory variables.
Simulated data with linear trend, varying seasonal and 1 explanatory variable.
rng(1000)
model=struct;
model.trend=1;
model.trendb=[5,1000];
model.seasonal=102;
model.seasonalb=100*[2 4 0.1 8 0.001];
model.signal2noiseratio=10;
T=120;
Xall=1e+2*randn(T,1);
model.X=Xall;
model.Xb=100;
out=simulateTS(T,'model',model,'plots',1);
% Fit a model using just the first 100 obs
yall=out.y;
Tred=100;
y=yall(1:Tred);
X=Xall(1:Tred,:);
model=struct;
model.trend=1;
model.seasonal=102;
% Potential level shift position is investigated in positions:
% t=11, t=11, ..., t=T-11.
model.lshift=-1;
model.X=X;
out=LTSts(y,'model',model,'plots',1,'dispresults',true);
% Note that in this case all the 120 values of Xall are supplied and
% the number of forecasts is 20
model.X=Xall;
forecastTS(out,'model',model,'nfore',20)
 Forecast with autoregressive components and expl var.
Forecast with autoregressive components and expl var.
 Forecast with autoregressive components and expl var.
Forecast with autoregressive components and expl var.Simulated data with linear trend, varying seasonal and AR(2)
rng(1000)
model=struct;
model.trend=1;
model.trendb=[5,1000];
model.seasonal=102;
model.seasonalb=100*[2 4 0.1 8 0.001];
model.signal2noiseratio=10;
model.ARp=[1 2];
model.ARb=[0.2 0.7];
model.ARIMAX=true;
T=100;
out=simulateTS(T,'model',model,'plots',1);
% Fit a model imposing linear trend, seasonal component and AR(2)
y=out.y;
nfore=20;
Xall=1e+2*randn(T+nfore,1);
X=Xall(1:T,:);
model=struct;
model.trend=1;
model.seasonal=102;
% No level shift
model.lshift=0;
% Add a non important expl. variable
model.X=X;
model.ARp=[1 2];
out=LTSts(y,'model',model,'plots',1,'dispresults',true);
% Note that in this case all the 120 values of Xall are supplied and
% the number of forecasts is 20
model.X=Xall;
forecastTS(out,'model',model,'nfore',20)
Iterative search of sigmaeps depending on the desired signal2noise ratio.
After 1000 iterations, the value of signal2noise ratio closest to the desired one is 10.0005,
obtained with sigmaeps = 107955.6243
Coeff SE t pval
_________ _________ ________ __________
b_trend1 -16801 33939 -0.49503 0.62178
b_trend2 2117.5 953.27 2.2214 0.028835
b_cos1 -32427 21648 -1.4979 0.13766
b_sin1 51362 27551 1.8642 0.065548
b_cos2 6181.2 16773 0.36852 0.71335
b_sin2 -39328 22569 -1.7426 0.084824
b_auto 1 0.16847 0.064852 2.5978 0.01096
b_auto 2 0.64325 0.065699 9.7907 7.7762e-16
b_explX1 360.92 157.24 2.2954 0.024035
b_varaml 0.0016604 0.0088853 0.18687 0.85218
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
ans =
struct with fields:
signal: [120×1 double]
trend: [120×1 double]
seasonal: [120×1 double]
X: [100×10 double]
lshift: 0
XAR: [120×1 double]
Xexpl: [120×0 double]
confband: [120×2 double]
datesnumeric: [120×1 double]
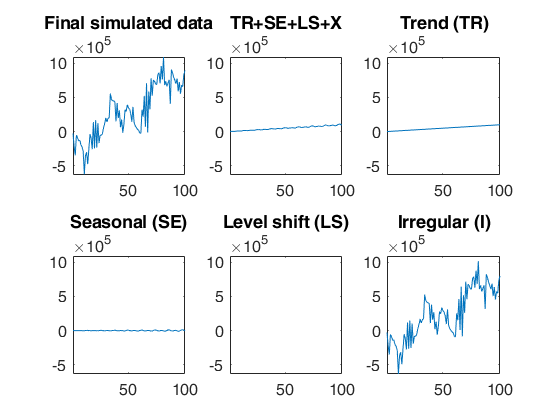
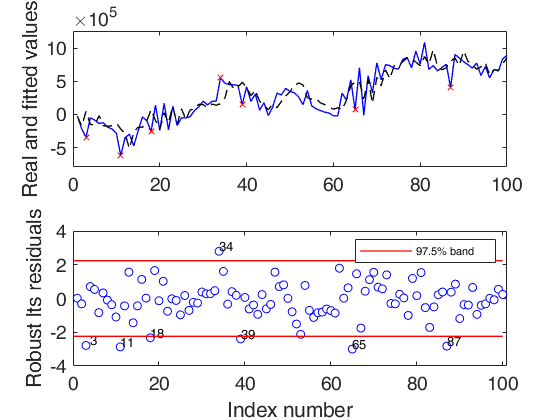
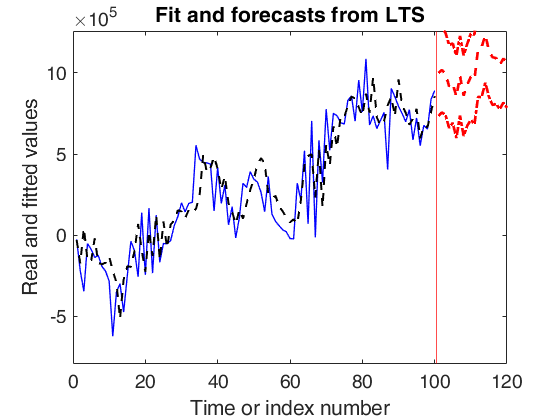
Check accuracy of forecasts.
AR(2) model with fixed seasonal
rng(1000)
model=struct;
model.trend=1;
model.trendb=[5,0.01];
model.seasonal=2;
model.seasonalb=0.1*[2 4 0.1 2];
model.signal2noiseratio=10;
model.ARp=[1 2];
model.ARb=[0.2 0.3];
model.ARIMAX=true;
T=150;
out=simulateTS(T,'model',model,'plots',1);
yall=out.y;
% Fit a model imposing linear trend, seasonal component and AR(2)
y=out.y(1:100);
nfore=50;
model=struct;
model.trend=1;
model.seasonal=2;
% No level shift
model.lshift=0;
model.ARp=[1 2];
out=LTSts(y,'model',model,'plots',1,'dispresults',true);
% Note that in this case all the 120 values of Xall are supplied and
% the number of forecasts is 20
forecastTS(out,'model',model,'nfore',50,'conflev',0.75)
hold('on')
plot(1:length(yall),yall)
Input Arguments
outEST — A structure containing the output of routine LTSts.
Structure.
Structure containing the following fields.
| Value | Description |
|---|---|
B |
Matrix containing estimated beta coefficients, (including the intercept when options.intercept=true) standard errors, t-stat and p-values The content of matrix B is as follows: 1st col = beta coefficients The order of the beta coefficients is as follows: 1) trend elements (if present). If the trend is of order two there are r+1 coefficients if the intercept is present otherwise there are just r components; 2) linear part of seasonal component 2, 4, 6, ..., s-2, s-1 coefficients (if present); 3) coefficients associated with the matrix of explanatory variables and/or autoregressive part which have a potential effect on the time series under study (X); 4) non linear part of seasonal component, that is varying amplitude. If varying amplitude is of order k there are k coefficients (if present); 5) level shift component (if present). In this case there are two coefficients, the second (which is also the last element of vector beta) is an integer which specifies the time in which level shift takes place and the first (which is also the penultimate element of vector beta) is a real number which identifies the magnitude of the upward (downward) level shift; 2nd col = standard errors; 3rd col = t-statistics; 4th col = p values. |
posLS |
scalar associated with best tentative level shift position. If this field does not exist, forecasts are done assuming no level shift. |
invXX |
. p-by-p, square matrix. If the model is linear out.invXX is equal to (X'X)^{-1}, else out.invXX is equal to (A'A)^{-1} where A is the matrix of partial derivatives. More precisely: a_{i,j}=\frac{\partial \eta_i(x_i, \hat \beta)}{\partial \hat \beta_j} where \begin{eqnarray} y_i & = & \eta(x_i,\beta)+ \epsilon_i \\ & = & \eta_i +\epsilon_i \\ & = & \eta(x_i,\hat \beta)+ e_i \\ & = & \hat \eta_i + e_i \end{eqnarray} |
yhat |
vector of n fitted values after final (NLS=non linear least squares) step: (\hat \eta_1, \hat \eta_2, \ldots, \hat \eta_T)' |
scale |
Final scale estimate of the residuals \hat \sigma = cor \times \sum_{i \in S_m} [y_i- \eta(x_i,\hat \beta)]^2/(m-p) where S_m is a set of cardinality m which contains the units not declared as outliers and p is the total number of estimated parameters and cor is a correction factor to make the estimator consistent. REMARK: structure outEST can be conveniently created by function LTSts. |
Data Types: struct
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'model', model
, 'nfore',12
, 'conflev',0.999
, 'plots',1
, 'titl','Plot with two wedges'
, 'StartDate',[2016,3]
, 'FileNameOutput',['C:' filesep 'myoutput' fielsep 'savesimdata.txt']
, 'dispresults',true
model
—model type.structure.
A structure which specifies the model used to simulate the time series. The structure contains the following fields:
| Value | Description |
|---|---|
trend |
scalar (order of the trend component). trend = 1 implies linear trend with intercept, trend = 2 implies quadratic trend, etc. If this field is empty the simulated time series will not contain a trend. The default value of model.trend is 1. |
s |
scalar greater than zero which specifies the length of the seasonal period. For monthly data (default) s=12, for quarterly data s=4, ... The default value of model.s is 12 (that is monthly data are assumed) |
seasonal |
scalar (integer specifying number of frequencies, i.e. harmonics, in the seasonal component. Possible values for seasonal are 1, 2, ..., [s/2], where [s/2]=floor(s/2). For example: if seasonal = 1 (default) we have: \beta_1 \cos( 2 \pi t/s) + \beta_2 sin ( 2 \pi t/s); if seasonal = 2 we have: \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s) + \beta_3 \cos(4 \pi t/s) + \beta_4 \sin (4 \pi t/s). Note that when s is even the sine term disappears for j=s/2 and so the maximum number of trigonometric parameters is s-1. If seasonal is a number greater than 100 then it is possible to specify how the seasonal component grows over time. For example, seasonal = 101 implies a seasonal component which just uses one frequency which grows linearly over time as follows: (1+\beta_3 t)\times ( \beta_1 cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s)). For example, seasonal = 201 implies a seasonal component which just uses one frequency which grows in a quadratic way over time as follows: (1+\beta_3 t + \beta_4 t^2)\times( \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s)). If this field is an empty double (default) the simulated time series will not contain a seasonal component. |
X |
explanatory variables. Matrix of size (length(y)+nfore)-by-nexpl. If model.X is a matrix of size (length(y)+nfore)-by-nexpl, it contains the values of nexpl extra covariates which affect y for periods 1:(length(y)+nfore) where nfore is the requested number of forecasts. If this field is an empty double (default) there is no effect of explanatory variables. |
ARp |
vector with non negative integer numbers specifying the autoregressive components. For example: model.ARp=[1 2] means a AR(2) process; model.ARp=2 means just the lag 2 component; model.ARp=[1 2 5 8] means AR(2) + lag 5 + lag 8; model.ARp=0 (default) means no autoregressive component. |
ARtentout |
matrix of size r-by-2 containing the list of the units declared as outliers (first column) and corresponding fitted values (second column) or empty scalar. If model.ARtentout is not empty, when the autoregressive component is present, the y values which are used to compute the autoregressive component are replaced by model.tentout(:,2) for the units contained in model.tentout(:,1) |
Example: 'model', model
Data Types: struct
nfore
—number of forecasts.scalar.
Positive integer which defines the number of forecasts. The default value of nfore is 24.
Example: 'nfore',12
Data Types: double
conflev
—confidence level for the confidence bands.scalar.
A number between 0 and 1 which defines the confidence level which is used to produce the bands. The default value of conflev is 0.99.
Example: 'conflev',0.999
Data Types: double
plots
—Plots on the screen.scalar.
If plots == 1 a plot with the real time series with fitted values and forecasts (with confidence bands) will appear on the screen. This plot is tagged forecastTS.
The default value of plot is 0, that is no plot is shown on the screen.
If plots == 2 an additional plot which shows the contribution of the different underlying components to fitted and forecasts will also appear on the screen. This plot is tagged decompTS. In other terms, in this plot we show the contribution given to outFORE.signal by outFORE.trend, outFORE.seasonal, outFORE.lshift, outFORE.Xexpl and outFORE.XAR. In all the underlying components (except trend) we impose the sum to zero constraint in the period 1:Tround where Tround=length(y)-mod(length(y),s);
Example: 'plots',1
Data Types: double
titl
—Title.string.
A label for the title (default: 'Double wedge plot').
Example: 'titl','Plot with two wedges'
Data Types: char
StartDate
—The time of the first observation.numeric vector of length 2.
Vector with two integers, which specify a natural time unit and a (1-based) number of samples into the time unit. For example, if model.s=12 (that is the data are monthly) and the first observation starts in March 2016, then StartDate=[2016,3]; Similarly, if models.s=4 (that is the data are quarterly) and the first observation starts in the second quarter or year 2014, then StartData=[2014,2]. The information in option StartDate will be used to create in the output the dates inside the time series object.
Example: 'StartDate',[2016,3]
Data Types: double
FileNameOutput
—save simulated time series to txt file.character.
If FileNameOutput is empty (default) nothing is saved on the disk, else FileNameOutput will contain the path where to save the file on the disk.
Example: 'FileNameOutput',['C:' filesep 'myoutput' fielsep 'savesimdata.txt']
Data Types: Character
dispresults
—Display results of final fit.boolean.
If dispresults is true, labels of coefficients, estimated coefficients, standard errors, tstat and p-values are shown on the screen in a fully formatted way. The default value of dispresults is false.
Example: 'dispresults',true
Data Types: logical
Output Arguments
outFORE — description
Structure
Structure which contains the following fields:
| Value | Description |
|---|---|
signal |
vector of length (length(y)+nfore) containing predictive values in sample and out of sample. Predictive values = TR+SE+XAR+Xexpl+LS. Note that outFORE.signal =outFORE.trend+outFORE.seasonal +outFORE.lshift+outFORE.Xexpl+outFORE.XAR. The single components which make up the overall estimated values are given below. |
trend |
vector of length (length(y)+nfore) containing estimated trend (TR) in sample and out of sample. If this component is not present, it is equal to 0. |
seasonal |
vector of length (length(y)+nfore) containing estimated seasonal component (SE) in sample and out of sample. If this component is not present, it is equal to 0. |
lshift |
vector of length (length(y)+nfore) containing level shift (LS) in sample and out of sample. If this component is not present, it is equal to 0. |
Xexpl |
vector of length (length(y)+nfore) containing the effect of the explanatory variables (Xexpl). If this component is not present, it is equal to 0. |
XAR |
vector of length (length(y)+nfore) containing the effect of the explanatory variables (Xexpl). If this component is not present, it is equal to 0. |
confband |
matrix of size (length(y)+nfore)-by-2 containing lower and upper confidence bands of the forecasts. The confidence level of the bands is specified in input parameter conflev. Note that the first length(y) rows of this matrix are equal to NaN. |
datesnumeric |
vector of length (length(y)+nfore) containing the dates in numeric format. |
X |
data matrix X containing trend, seasonal, expl and lshift, if the model is linear or linearized version of \eta(x_i, \beta) if the model is non linear containing in the columns partial derivatives evaluated in correspondence of outEST.B(:,1) with respect to each parameter. In other words, the i,j-th element of outFORE.X is \frac{\partial \eta_i(x_i, \hat \beta)}{\partial \hat \beta_j} j=1, 2, \ldots, p, i=1, 2, \ldots, T. The size of this matrix is: T-by-p The field is present only if option yxsave is set to 1. |
References
Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". [RPRH]
See Also
LTSts
|
wedgeplot
|
simulateTS
|
LTStsVarSel