genSigmaGPCM
genSigmaGPCM generates covariance matrix for the 14 Gaussian Parsimonious Clustering Models
Syntax
S=genSigmaGPCM(v, k, pa)example
Examples
 Covariance matrices contours for the 14 models.
Covariance matrices contours for the 14 models.
 Covariance matrices contours for the 14 models.
Covariance matrices contours for the 14 models.Two dimensions
v=2;
% 3 groups
k=3;
pa=struct;
models={'VVE','EVE','VVV','EVV','VEE','EEE','VEV','EEV','VVI',...
'EVI','VEI','EEI','VII','EII'};
% Specify the colors for the ellipses
col='rbk';
% if withseed is true the same plot is always obtained otherwise every time
% a different plot is obtained
withseed=true;
close all
% These numbers are those which better exemplify the characteristics of the
% 14 specifications.
seeds=[100 20 12 209 51 6 76 8 9 29 111 12 130 14];
pa=struct;
for j=1:length(models)
if withseed==true
rng(seeds(j))
end
pa.pars=models{j};
S=genSigmaGPCM(v, k, pa);
subplot(4,4,j)
hold('on')
for i=1:k
ellipse(zeros(v,1), S(:,:,i),0.95,col(i));
end
axis equal
legend('off')
title(pa.pars)
end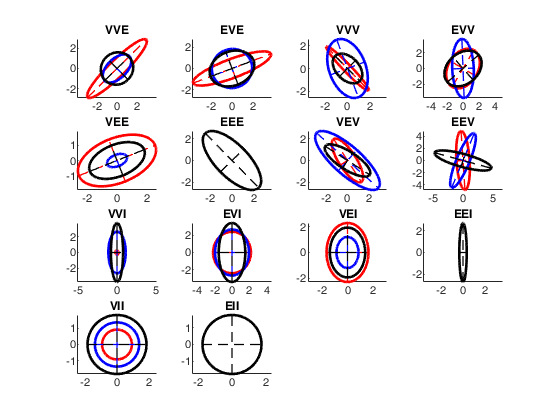
Related Examples
 Covariance matrices contours for the 14 models (with different locations).
Covariance matrices contours for the 14 models (with different locations).
 Covariance matrices contours for the 14 models (with different locations).
Covariance matrices contours for the 14 models (with different locations).Two dimensions
v=2;
% 3 groups
k=3;
models={'VVE','EVE','VVV','EVV','VEE','EEE','VEV','EEV','VVI',...
'EVI','VEI','EEI','VII','EII'};
% Specify the colors for the ellipses
col='rbk';
% if withseed is true the same plot is always obtained otherwise every time
% a different plot is obtained
withseed=true;
close all
% These numbers are those which better exemplify the caractheristics of the
% 14 specifications.
seeds=[100 20 12 209 51 6 76 8 9 29 111 12 130 14];
pa=struct;
for j=1:length(models)
if withseed==true
rng(seeds(j))
end
modeltype=models{j};
pa.pars=modeltype;
S=genSigmaGPCM(v, k, pa);
subplot(4,4,j)
hold('on')
for i=1:k
cen=zeros(v,1)+i*2;
ellipse(cen, S(:,:,i),0.95,col(i));
end
axis equal
legend('off')
title(modeltype)
end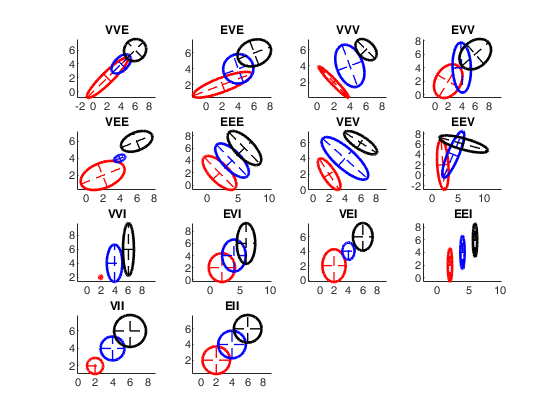
Input Arguments
v — number of dimensions (variables).
Scalar.
Desired number of variables.
Data Types: int16|int32|int64|single|double
k — number of groups (components).
Scalar.
Desired number of groups.
Data Types: int16|int32|int64|single|double
pa — Constraints to apply and model specification.
Structure.
Structure containing the following fields:
| Value | Description |
|---|---|
pars |
type of Gaussian Parsimonious Clustering Model. Character. A 3 letter word in the set: 'VVE','EVE','VVV','EVV','VEE','EEE','VEV','EEV','VVI', 'EVI','VEI','EEI','VII','EII'. The field pa.pars is compulsory. All the other fields are non necessary. If they are not present they are set to their default values. |
exactrestriction |
boolean. If pa.exactrestriction is true the covariance matrices have to be generated with the exact values of the restrictions specified in pa.cdet, pa.shw and pa.swb. In order to reach this purpose, this procedure ensures to generate shape matrices in which at least one ratio of the elements inside each component is greater or equal than that specified is pa.shw and at least one ratio among the ordered elements of each shape matrix is greater or equal tahn pa.shb. The successive application of routine restrSgimaGPCM guarrantes that the inequalites become equalities. The default value of pa.exaxtrestriction is false therefore covariance matrices are generated without implying any constraint. If pa.exactrestriction is true covariance matrices are generated with: 1) max ratio between determinants equal to pa.cdet (if pa.cdet is specififed); 2) at least a ratio between the elements of each shape matrix greater or equal than pa.shw (if pa.shw is specififed); 3) max ratio between the ordered elements of each shape matrices greater or equal than pa.shb). |
cdet |
scalar in the interval [1 Inf) which specifies the the restriction which has to be applied to the determinants. This field is used just if pa.exactrestriction is true. |
shw |
scalar in the interval [1 Inf) which specifies the the restriction which has to be applied to the elements of the shape matrices inside each group. This field is used just if pa.exactrestriction is true. |
shb |
scalar in the interval [1 Inf) which specifies the the restriction which has to be applied to the ordered elements of the shape matrices across groups. This field is used just if pa.exactrestriction is true. |
Data Types: struct
Output Arguments
More About
Additional Details
Generate covariance matrices from the 14 parsimonious Gaussian clustering models (GPCM).
References
Celeux, G., Govaert, G. (1995), Gaussian parsimonious clustering models, "Pattern Recognition", 28, pp. 781-793.