tclustICplot

tclustICplot plots information criterion as a function of c and k

expand all in page

Syntax

Description

tclustICplot takes as input the output of function tclustIC (that is a series of matrices which contain the values of the information criteria BIC/ICL/CLA for different values of k and c) and plots them as function of c or of k. The plot enables interaction in the sense that, if option databrush has been activated, it is possible to click on a point in the plot and to see the associated classification in the scatter plot matrix.

example

tclustICplot(IC) Plot BIC, ICL and CLA for for Geyser data with all default options.

example

tclustICplot(IC, Name, Value) Example of the use of option datatooltip (all default options).

Examples

expand all

  • Plot BIC, ICL and CLA for for Geyser data with all default options.

    • Y=load('geyser2.txt');
% Make sure (whenever possible) that units 15, 30 and 69 are inside
% groups which have labels respectively equal to 1, 2 and 3.
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out);
    k=1
k=2
k=3
k=4
k=5
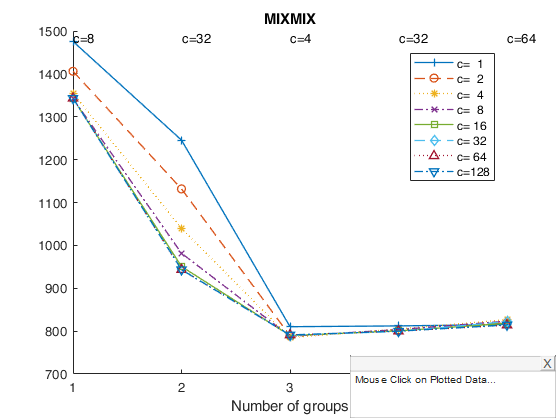
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Example of the use of option datatooltip (all default options).

    • Gives the user the possibility of clicking on the different points and have information about 1) value of k which has been selected 2) value of c which has been selected 3) values of the information criterion 4) frequency distribution of the associated classification 

    Y=load('geyser2.txt');
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out,'datatooltip',1);

    Related Examples

    expand all

  • Example of the use of option datatooltip (personalized options).

    • Gives the user the possibility of clicking on the different points and have information about the selected, the step of entry into the subset and the associated label. 

    datatooltip = struct;
% In this example the style of the datatooltip is 'datatip'. Click on a
% point when the ICplot is displayed.
datatooltip.DisplayStyle = 'datatip';
Y=load('geyser2.txt');
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out,'datatooltip',datatooltip);

  • Simultaneous datatooltip with all 3 plots (MIXMIX, MIXCLA and CLACLA).

    • Y=load('geyser2.txt');
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out,'whichIC','ALL');

  • Interactive example 1. databrushing from the ICplot.

    • % Use all default options for databrush (brush just once)
Y=load('geyser2.txt');
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out,'databrush',1);

  • Interactive example 2. Repeated databrushing from the ICplot.

    • % enable repeated brushing and show boxplots of groups inside diag of spm
databrush=struct;
% Set the shape of the brush
databrush.selectionmode='Rect';
% Enable repeated brushing
databrush.persist='on';
% Include x and y coordinates of brushed solutions inside ICplot
databrush.Label='on';
% Remove x and y coordinated just after btushing
databrush.RemoveLabels='on';
% show boxplots of the groups instead of histograms on the main
% diagonal of the spm
databrush.dispopt='box';
Y=load('geyser2.txt');
UnitsSameGroup=[15 30 69];
out=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1,'UnitsSameGroup',UnitsSameGroup);
tclustICplot(out,'databrush',databrush);

    Input Arguments

    expand all

    IC — Information criterion to use. Structure.

    It contains the following fields.

    Value Description
    CLACLA

    matrix of size length(kk)-times length(cc) containinig the values of the penalized classification likelihood (CLA).

    This field is linked with out.IDXCLA.
    IDXCLA

    cell of size length(kk)-times length(cc). Each element of the cell is a vector of length n containinig the assignment of each unit using the classification model.

    Remark: fields CLACLA and IDXCLA are linked together.

    CLACLA and IDXCLA are compulsory just if optional input argument 'whichIC' is 'CLACLA' or 'ALL'
    MIXMIX

    matrix of size length(kk)-times length(cc) containinig the value of the penalized mixture likelihood (BIC). This field is linked with out.IDXMIX.
    MIXCLA

    matrix of size length(kk)-times length(cc) containinig the value of the ICL. This field is linked with out.IDXMIX.
    IDXMIX

    cell of size length(kk)-times length(cc). Each element of the cell is a vector of length n containinig the assignment of each unit using the mixture model.

    Remark 1: fields MIXMIX and IDXMIX are linked together.

    MIXMIX and IDXMIX are compulsory just if optional input argument 'whichIC' is 'CLACLA' or 'ALL'.

    Remark 2: fields MIXCLA and IDXMIX are linked together.

    MIXCLA and IDXMIX are compulsory just if optional input argument 'whichIC' is 'MIXCLA' or 'ALL'.
    kk

    vector containing the values of k (number of components) which have been considered.
    cc

    scalar or vector containing the values of c (values of the restriction factor) which have been considered.
    Y

    original n-times-v data matrix on which the IC (Information criterion) has been computed
    alpha

    scalar or vector containing the values of trimming which have been considered. If input structure IC comes from tclustreg, then trimming refers to first level trimming (likelihood trimming).
    nameY

    cell of length(size(Y,2)) containing the names of the variables of original matrix Y

    Data Types: struct

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'whichIC','ALL' , 'tag','myplot' , 'ylimy',[0 100] , 'datatooltip','' , 'databrush',1 , 'nameY',{'myY1', 'myY2'}

    whichIC —character which specifies the information criterion to use in the plot.character.

    Possible values for whichIC are: 'CLACLA' = in this case best solutions are referred to the classification likelihood.

    'MIXMIX' = in this case in this case best solutions are referred to the mixture likelihood (BIC).

    'MIXCLA' = in this case in this case best solutions are referred to ICL.

    'ALL' = in this case best solutions both three solutions using classification and mixture likelihood are produced.

    In output structure out all the three matrices out.MIXMIXbs, out.CLACLAbs and out.MIXCLAbs are given.

    The default value of 'whichIC' is 'ALL'

    Example: 'whichIC','ALL'

    Data Types: character

    tag —Personalized tag.string.

    String which identifies the handle of the plot which is about to be created. The default is to use tag 'pl_IC'.

    Note that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created.

    Example: 'tag','myplot'

    Data Types: char

    ylimy —Min and Max of the y axis.vector.

    Vector with two elements controlling minimum and maximum of the y axis.

    If ylimy is empty automatic scale is used

    Example: 'ylimy',[0 100]

    Data Types: double

    datatooltip —interactive clicking.empty value (default) | structure.

    The default is datatooltip=''.

    If datatooltip = 1, the user can select with the mouse a solution in order to have the following information: 1) value of k which has been selected 2) value of c which has been selected 3) values of the information criterion 4) frequency distribution of the associated classification If datatooltip is a structure it may contain the following the fields

    Value Description
    DisplayStyle

    Determines how the data cursor displays. datatip | window.

    - datatip displays data cursor information in a small yellow text box attached to a black square marker at a data point you interactively select.

    - window displays data cursor information for the data point you interactively select in a floating window within the figure.
    SnapToDataVertex

    Specifies whether the data cursor snaps to the nearest data value or is located at the actual pointer position. on | off.

    - on data cursor snaps to the nearest data value - off data cursor is located at the actual pointer position.

    (see the MATLAB function datacursormode or the examples below). Default values are datatooltip.DisplayStyle = 'Window' and datatooltip.SnapToDataVertex = 'on'.

    Example: 'datatooltip',''

    Data Types: scalar double or struct

    databrush —interactive mouse brushing.empty value, scalar | structure.

    If databrush is an empty value (default), no brushing is done. The activation of this option (databrush is a scalar or a structure) enables the user to select a set of values of IC in the current plot and to see the corresponding classification highlighted in the scatter plot matrix (spm). If spm does not exist it is automatically created. Please, note that the window style of the other figures is set equal to that which contains the IC plot. In other words, if the IC plot is docked all the other figures will be docked too.

    DATABRUSH IS A SCALAR. If databrush is a scalar the default selection tool is a rectangular brush and it is possible to brush only once (that is persist='').

    DATABRUSH IS A STRUCTURE. If databrush is a structure, it is possible to use all optional arguments of function selectdataFS and the following optional arguments: - databrush.persist = repeated brushing enabled. Persist is an empty value or a scalar containing the strings 'on' or 'off'.

    The default value of persist is '', that is brushing is allowed only once.

    If persist is 'on' or 'off' brushing can be done as many time as the user requires.

    If persist='on' then the unit(s) currently brushed are added to those previously brushed. it is possible, every time a new brushing is done, to use a different color for the brushed solutions.

    If persist='off' every time a new brush is performed units previously brushed are removed.

    - databrush.Label = add labels (i.e. x=value of k and y=values of IC) of brushed solutions in the ICplot.

    Character. [] (default) | '1'.

    - dispopt = string which controls how to fill the diagonals in the scatterplot matrix of the brushed solutions. Set dispopt to 'hist' (default) to plot histograms, or 'box' to plot boxplots.

    Example: 'databrush',1

    Data Types: single | double | struct

    nameY —variable labels.cell array.

    Cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ..., Yv.

    Example: 'nameY',{'myY1', 'myY2'}

    Data Types: cell

    Output Arguments

    expand all

    References

    Cerioli, A., Garcia-Escudero, L.A., Mayo-Iscar, A. and Riani M. (2017), Finding the Number of Groups in Model-Based Clustering via Constrained Likelihoods, "Journal of Computational and Graphical Statistics", pp. 404-416, https://doi.org/10.1080/10618600.2017.1390469

    Hubert L. and Arabie P. (1985), Comparing Partitions, "Journal of Classification", Vol. 2, pp. 193-218.

    See Also

    | |

    This page has been automatically generated by our routine publishFS