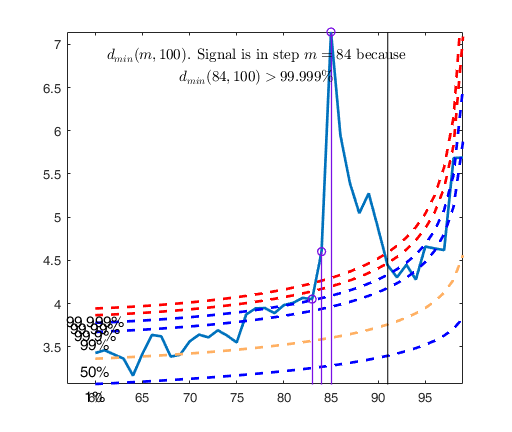
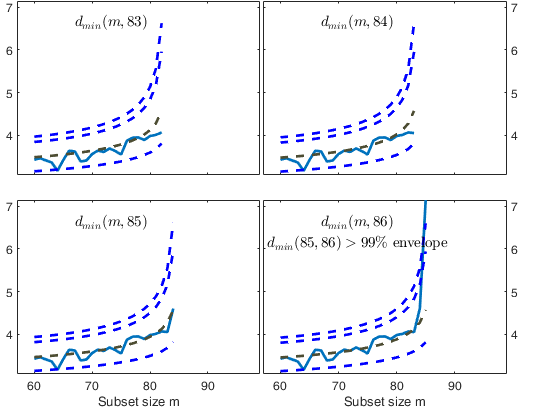
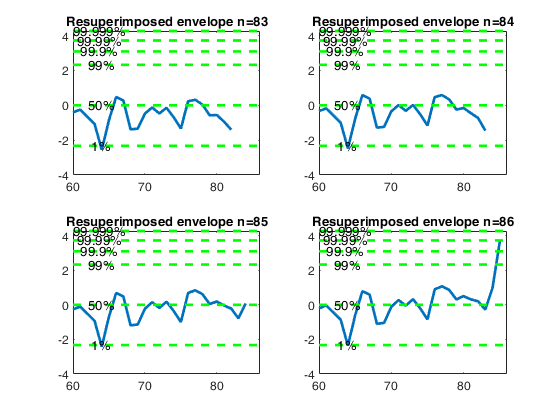
Let $d^2_i(m )$ and $d_{\mbox{min}}(m)$ be respectively the deletion distance for unit $i$ based on a subset of size $m$ and $d_{\mbox{min}}(m)$ the min. Mahalanobis distance in the forward search at step m. Testing for outliers requires a reference distribution for $d^2_i(m )$ in and hence for $d_{\mbox{min}}(m)$ in (\ref{min}). When $\Sigma$ is estimated from all $n$ observations, the squared statistics have an $F$ distribution.

However, the estimate $\hat{\Sigma}(m)$ in the search uses the central $m$ out of $n$ observations, so that the variability is underestimated.

The consistency factor $c(m,n)$ given below

$$c(m,n)=\frac{n}{m} C_{v+2} \{C_{v}^{-1} (m/n) \}$$

where $C_r$ is the c.d.f. of the $\chi^2$ distribution on $r$ degrees of freedom, allows for estimation from this truncated distribution, providing an approximately unbiased estimate of $\Sigma$.

We can treat the distribution of the rescaled deletion Mahalanobis distance $c(m,n)d_{\mbox{min}}^2(m)$ as a squared deletion distance on $m-1$ degrees of freedom, whose distribution is (Atkinson Riani and Cerioli, 2004; pp. 43-44) $$\begin{equation}\label{F} \frac{m^2-1}{m(m-v)} F_{v,m-v}, \end{equation}$$ The distribution of the rescaled min Mahalanobis distance $c(m,n) d_{\mbox{min}}^2(m)$ of a subset of size $m$ constructed in such a way that the centroid and covariance matrix of the subset are taken using the units having the $m$ smallest Mahalanobis distances can be treated as the distribution of the $(m+1)$th order statistic from ($F_{v,m-v}$).

The results of order statistics $Y_{(1)}$, $Y_{(2)}$, $\cdots$, $Y_{(n)}$ from a sample of size $n$ from a distribution with CDF $G(y)$, state that $$\begin{equation} \label{orderstat} P\{Y_{(m+1)} \le y \} = P \left\{ F_{2(n-m),2(m+1)} > \frac{1-G(y)}{G(y)} \times \frac{m+1}{n-m} \right\} \end{equation}$$ Given that in our case $G(y)$ is the CDF of the $F_{v,m-v}$ we can rewrite this equation as $$\begin{eqnarray*} && P\{d_{\mbox{ min}}^2(m) \leq \widehat{ d_{\mbox{min}}^2(m)} \} = \\ && 1- F_{2(n-m),2(m+1)} \left( \left( \frac{1}{ F_{v,m-v} \left( \frac{m(m-v)}{m^2-1 } c(m,n) d_{\mbox{min}}^2(m) \right) }-1 \right) \frac{m+1}{n-m} \right) \end{eqnarray*}$$ where $F_{a,b}(y)$ is the CDF of the $F$ distribution with $a$ and $b$ degrees of freedom evaluated in $y$.

The value of the min. Mahalanobis distance transformed in normal coordinates computed by this routine is nothing but

$$\Phi^{-1} \left( P\left\{ d_{\mbox{min}}^2(m) \leq \widehat{ d_{\mbox{min}}^2(m)} \right\} \right)$$

where $\Phi^{-1}$ is the inverse of the CDF of the standard normal distribution.