FSReda
FSReda enables to monitor several quantities in each step of the forward search
Description
Examples
Related Examples
Example with artificial dataset.
Example with artificial dataset.
n=100;
p=8;
state=1;
randn('state', state);
X=randn(n,p);
y=randn(n,1);
y(1:10)=y(1:10)+5;
% Run the forward search with Exploratory Data Analysis purposes
% LMS using 10000 subsamples
[outLXS]=LXS(y,X,'nsamp',10000);
% Forward Search
[out]=FSReda(y,X,outLXS.bs);
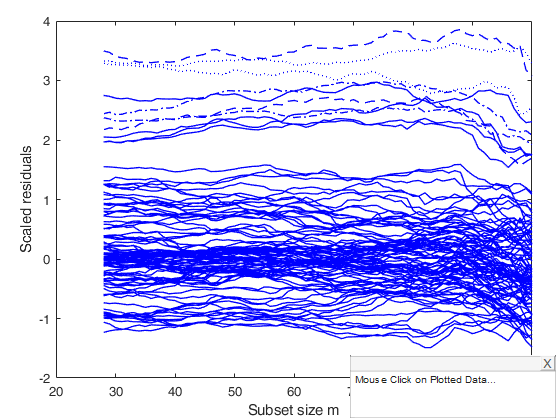
%The monitoring residuals plot shows a set of positive residuals which
%starting from the central part of the search tend to have a residual much
%larger than that of the other units.
resfwdplot(out);
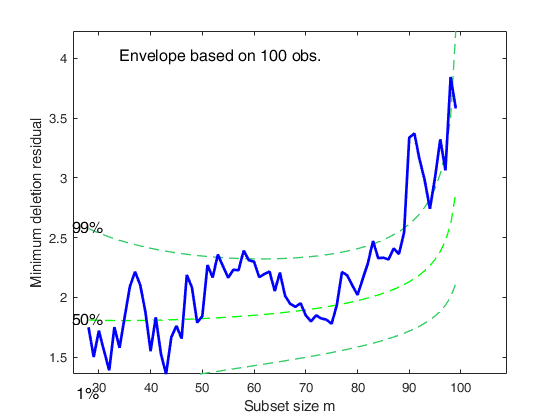
%The minimum deletion residual from m=90 starts going above the 99% threshold.
mdrplot(out);
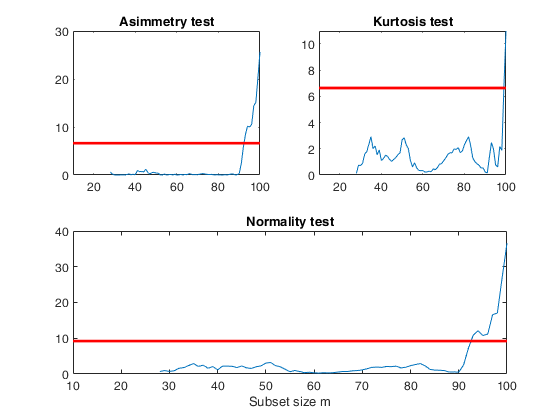
%The curve which monitors the normality test shows a sudden big increase with the outliers are included
figure;
lwdenv=2;
xlimx=[10 100];
subplot(2,2,1);
plot(out.nor(:,1),out.nor(:,2));
title('Asimmetry test');
xlim(xlimx);
quant=chi2inv(0.99,1);
v=axis;
line([v(1),v(2)],[quant,quant],'color','r','LineWidth',lwdenv);
subplot(2,2,2)
plot(out.nor(:,1),out.nor(:,3))
title('Kurtosis test');
xlim(xlimx);
v=axis;
line([v(1),v(2)],[quant,quant],'color','r','LineWidth',lwdenv);
subplot(2,2,3:4)
plot(out.nor(:,1),out.nor(:,4));
xlim(xlimx);
quant=chi2inv(0.99,2);
v=axis;
line([v(1),v(2)],[quant,quant],'color','r','LineWidth',lwdenv);
title('Normality test');
xlabel('Subset size m');Total estimated time to complete LMS: 0.05 seconds Warning: The opengl function will be removed in a future release. Use the rendererinfo function instead.
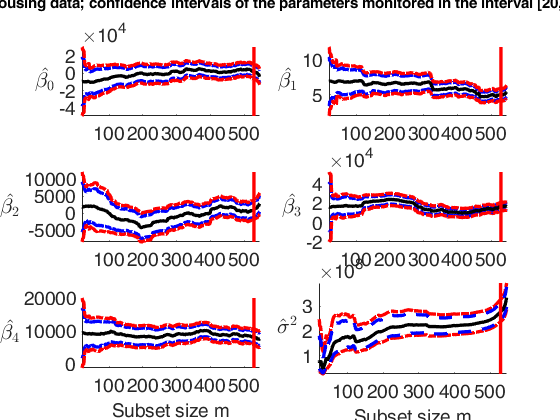
Monitoring of 95 per cent and 99 per cent confidence intervals of
beta and sigma2.
Monitoring of 95 per cent and 99 per cent confidence intervals of
beta and sigma2.
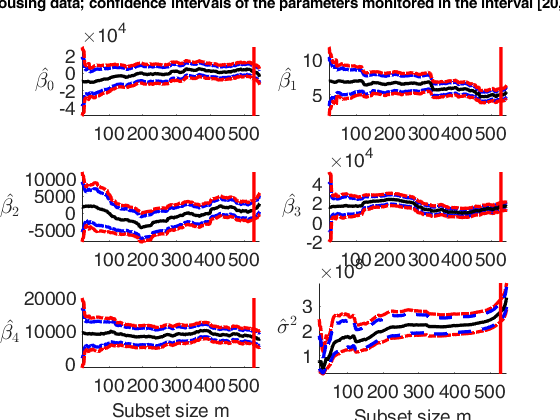
% House price data
load hprice.txt;
n=size(hprice,1);
y=hprice(:,1);
X=hprice(:,2:5);
outFSR=FSR(y,X,'plots',0,'msg',0);
dout=n-length(outFSR.ListOut);
% init = point to start monitoring diagnostics along the FS
init=20;
[outLXS]=LXS(y,X,'nsamp',10000);
outEDA=FSReda(y,X,outLXS.bs,'conflev',[0.95 0.99],'init',init);
p=size(X,2)+1;
% Set font size, line width and line style
figure;
lwd=2.5;
FontSize=14;
linst={'-','--',':','-.','--',':'};
nr=3;
nc=2;
xlimL=init; % lower value fo xlim
xlimU=n+1; % upper value of xlim
close all
for j=1:p
subplot(nr,nc,j);
hold('on')
% plot 95% and 99% HPD trajectories
plot(outEDA.Bols(:,1),outEDA.betaINT(:,1:2,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','b')
plot(outEDA.Bols(:,1),outEDA.betaINT(:,3:4,j),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% plot estimate of beta1_j
plot(outEDA.Bols(:,1),outEDA.Bols(:,j+1)','LineStyle',linst{1},'LineWidth',lwd,'Color','k')
% Set ylim
ylimU=max(outEDA.betaINT(:,4,j));
ylimL=min(outEDA.betaINT(:,3,j));
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
ylabel(['$\hat{\beta_' num2str(j-1) '}$'],'Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
if j>(nr-1)*nc
xlabel('Subset size m','FontSize',FontSize);
end
end
% Subplot associated with the monitoring of sigma^2
subplot(nr,nc,6);
hold('on')
% 99%
plot(outEDA.sigma2INT(:,1),outEDA.sigma2INT(:,4:5),'LineStyle',linst{4},'LineWidth',lwd,'Color','r')
% 95%
plot(outEDA.sigma2INT(:,1),outEDA.sigma2INT(:,2:3),'LineStyle',linst{2},'LineWidth',lwd,'Color','b')
% Plot rescaled S2
plot(outEDA.S2(:,1),outEDA.S2(:,4),'LineWidth',lwd,'Color','k')
ylabel('$\hat{\sigma}^2$','Interpreter','LaTeX','FontSize',20,'rot',-360);
set(gca,'FontSize',FontSize);
% Set ylim
ylimU=max(outEDA.sigma2INT(:,5));
ylimL=min(outEDA.sigma2INT(:,4));
ylim([ylimL ylimU])
% Set xlim
xlim([xlimL xlimU]);
% Add vertical line in correspondence of the step prior to the
% entry of the first outlier
line([dout; dout],[ylimL; ylimU],'Color','r','LineWidth',lwd);
xlabel('Subset size m','FontSize',FontSize);
% Add multiple title
suplabel(['Housing data; confidence intervals of the parameters monitored in the interval ['...
num2str(xlimL) ',' num2str(xlimU) ...
']'],'t');
disp(['The vertical lines are located in the' ...
' step prior to the inclusion of the first outlier'])Total estimated time to complete LMS: 0.24 seconds ------------------------------ Warning: Number of subsets without full rank equal to 38.3% m=100 m=200 m=300 m=400 m=500 The vertical lines are located in the step prior to the inclusion of the first outlier
Example to compute REML single weights for the units excluded
from the search at each step using wREML=true.
Example to compute REML single weights for the units excluded
from the search at each step using wREML=true.
load('loyalty.mat');
y = loyalty{:,end};
X = loyalty{:,1};
tit = sprintf('Loyalty data');
xla = 'Number of visits';
yla = 'Amount spent (in Euros)';
n = size(X, 1);
p = size(X, 2);
% LXS and FSReda
[outLXS]=LXS(y,X,'nsamp',1000);
[out] = FSReda(y, X, outLXS.bs, 'intercept', false, 'wREML', true);
% plot solution overwriting the RES output for simplicity
out.RES = out.wREML;
resfwdplot(out);
ylabel('REML weights FS');Total estimated time to complete LMS: 0.01 seconds m=100 m=200 m=300 m=400 m=500 Warning: The opengl function will be removed in a future release. Use the rendererinfo function instead.
Input Arguments
Output Arguments
References
Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.