FSRbsb
FSRbsb returns the units belonging to the subset in each step of the forward search
Description
Examples
FSRbsb with all default options.
load('fishery');
y=fishery{:,2};
X=fishery{:,1};
[out]=LXS(y,X,'nsamp',10000);
Un = FSRbsb(y,X,out.bs);
 Monitoring the units belonging to subset.
Monitoring the units belonging to subset.
 Monitoring the units belonging to subset.
Monitoring the units belonging to subset.
state=1000;
randn('state', state);
n=100;
X=randn(n,3);
bet=[3;4;5];
y=3*randn(n,1)+X*bet;
y(1:20)=y(1:20)+15;
[outLMS]=LXS(y,X);
bsb=outLMS.bs;
% Store in matrix BB the units belonging to subset in each step of the forward search
[Un,BB] = FSRbsb(y,X,bsb);
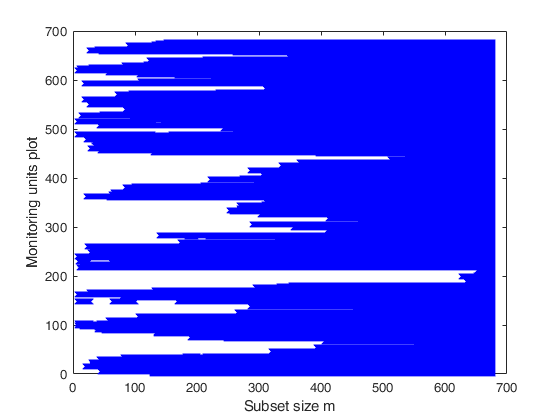
% Create the 'monitoring units plot'
figure;
seqr=[Un(1,1)-1; Un(:,1)];
plot(seqr,BB','bx');
xlabel('Subset size m');
ylabel('Monitoring units plot');
% The plot, which monitors the units belonging to subset in each step of
% the forward search, shows that apart from unit 11, which enters the
% search in step m=78, all the other contaminated units enter the search
% in the last 19 steps.
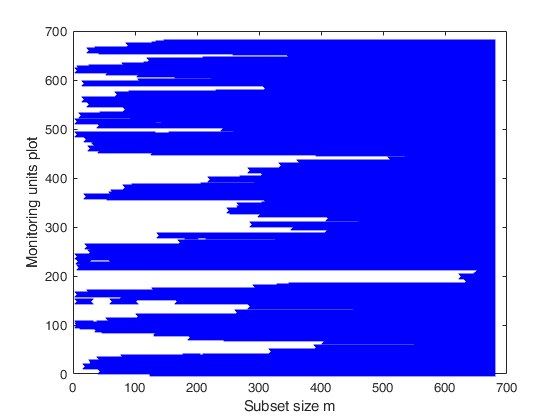
% if we consider the seed state=500, we obtain a plot showing that the
% 20 contaminated units enter the search in the final 20 steps.
state=500;
randn('state', state);
X=randn(n,3);
y=3*randn(n,1)+X*bet;
y(1:20)=y(1:20)+15;
[outLMS]=LXS(y,X);
bsb=outLMS.bs;
% Store in matrix BB the units belonging to subset in each step of the forward search
[Un,BB] = FSRbsb(y,X,bsb);
% Create the 'monitoring units plot'
figure;
seqr=[Un(1,1)-1; Un(:,1)];
plot(seqr,BB','bx');
xlabel('Subset size m');
ylabel('Monitoring units plot');
Total estimated time to complete LMS: 0.01 seconds Total estimated time to complete LMS: 0.01 seconds
Related Examples
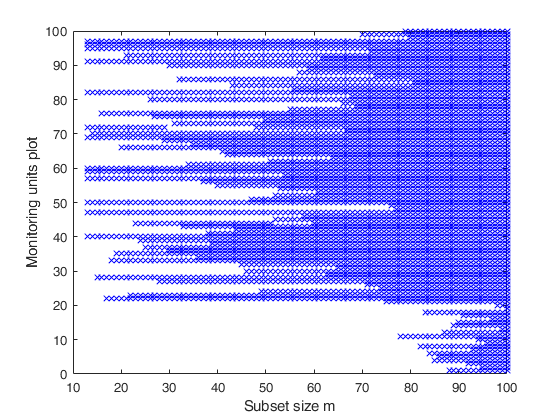
Example with monitoring from step 60.
load('fishery');
y=fishery{:,2};
X=fishery{:,1};
[out]=LXS(y,X,'nsamp',10000);
Un = FSRbsb(y,X,out.bs,'init',60);
FSR using a regression model without intercept.
load('fishery');
y=fishery{:,2};
X=fishery{:,1};
[out]=LXS(y,X);
bsb=out.bs;
[Un,BB] = FSRbsb(y,X,out.bs,'intercept',false);
FSR applied without doing any checks on y and X variables.
load('fishery');
y=fishery{:,2};
X=fishery{:,1};
[out]=LXS(y,X,'nsamp',10000);
[Un,BB] = FSRbsb(y,X,out.bs,'nocheck',true);
Input Arguments
y — Response variable.
Vector.
A vector with n elements that contains the response variable. y can be either a row or a column vector.
Data Types: single| double
X — Predictor variables.
Matrix.
Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.
Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: single| double
bsb — list of units forming the initial subset.
Vector | 0.
If bsb=0 then the procedure starts with p units randomly chosen else if bsb is not 0 the search will start with m0=length(bsb)
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'init',100 starts the search from step m=100
, 'intercept',false
, 'nocheck',true
, 'msg',true
, 'plots',1
init
—Search initialization.scalar.
It specifies the initial subset size to start monitoring units forming subset
Example: 'init',100 starts the search from step m=100
Data Types: double
intercept
—Indicator for constant term.true (default) | false.
Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.
Example: 'intercept',false
Data Types: boolean
nocheck
—Check input arguments.boolean.
If nocheck is equal to 1 no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.
Example: 'nocheck',true
Data Types: boolean
bsbsteps
—Save the units forming subsets in selected steps.vector | empty value.
It specifies for which steps of the fwd search it is necessary to save the units forming subset. If bsbsteps is 0 we store the units forming subset in all steps. If bsbsteps=[] or omitted, the default is to store the units forming subset in all steps if n<=5000, else to store the units forming subset at steps init and steps which are multiple of 100. For example, as default, if n=753 and init=6, units forming subset are stored for m=init, 100, 200, 300, 400, 500 and 600.
Example: 'bsbsteps',[100 200] stores the unis forming
subset in steps 100 and 200.
Data Types: double
msg
—Level of output to display.boolean.
It controls whether to display or not messages on the screen If msg==true (default) messages are displayed on the screen about step of the fwd search else no message is displayed on the screen.
Example: 'msg',true
Data Types: boolean
plots
—Plot on the screen.scalar.
If plots=1 the monitoring units plot is displayed on the screen. The default value of plots is 0 (that is no plot is produced on the screen).
Example: 'plots',1
Data Types: double
Output Arguments
Un —Units included in each step.
Matrix
(n-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the search.
REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one.
Un(1,2), for example, contains the unit included in step init+1.
Un(end,2) contains the units included in the final step of the search.
BB —Units belonging to subset in each step or selected steps.
Matrix
n-by-(n-init+1) or n-by-length(bsbsteps) matrix which contains the units belonging to the subset at each step (or in selected steps as specified by optional vector bsbsteps) of the forward search.
More precisely: BB(:,1) contains the units forming subset in step bsbsteps(1);
....;
BB(:,end) contains the units forming subset in step bsbsteps(end);
Row 1 of matrix BB is referred to unit 1;
......;
Row n of matrix BB is referred to unit n;
Units not belonging to subset are denoted with NaN.
References
Atkinson, A.C. and Riani, M. (2000), "Robust Diagnostic Regression Analysis", Springer Verlag, New York.