LXS
LXS computes the Least Median of Squares (LMS) or Least Trimmed Squares (LTS) estimators
Description
Examples
Related Examples
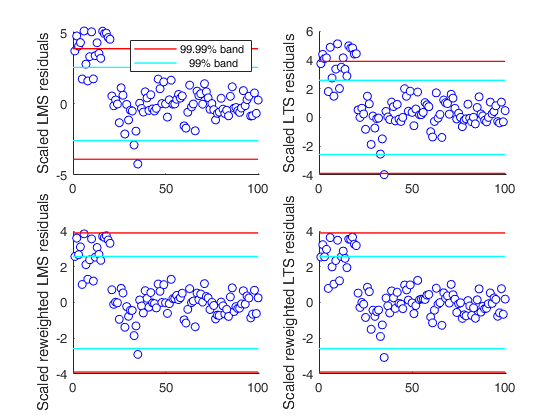
We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
We compare the output of different procedures: only the reweighted
LTS seems to detect half of the outlier with a Bonferroni
significance level.
close all;
state=100;
randn('state', state);
n=100;
X=randn(n,3);
bet=[3;4;5];
y=3*randn(n,1)+X*bet;
y(1:20)=y(1:20)+13;
% Define nominal confidence level
conflev=[0.99,1-0.01/length(y)];
% Define number of subsets
nsamp=3000;
% Define the main title of the plots
titl='';
% LMS with no reweighting
[outLMS]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1));
h=subplot(2,2,1)
laby='Scaled LMS residuals';
resindexplot(outLMS.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev)
% LTS with no reweighting
h=subplot(2,2,2);
[outLTS]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'lms',0);
laby='Scaled LTS residuals';
resindexplot(outLTS.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev);
% LMS with reweighting
[outLMSr]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'rew',1);
h=subplot(2,2,3);
laby='Scaled reweighted LMS residuals';
resindexplot(outLMSr.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev)
% LTS with reweighting
[outLTSr]=LXS(y,X,'nsamp',nsamp,'conflev',conflev(1),'rew',1,'lms',0);
h=subplot(2,2,4);
laby='Scaled reweighted LTS residuals';
resindexplot(outLTSr.residuals,'h',h,'title',titl,'laby',laby,'numlab','','conflev',conflev);
% By simply changing the seed to 543 (state=543), using a Bonferroni size of 1%, no unit is declared as outlier.Warning: Using 'state' to set RANDN's internal state causes RAND, RANDI, and
RANDN to use legacy random number generators. This syntax is not recommended.
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace the
old syntax.
Total estimated time to complete LMS: 0.01 seconds
h =
Axes with properties:
XLim: [0 1]
YLim: [0 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.1300 0.5838 0.3347 0.3412]
Units: 'normalized'
Use GET to show all properties
Total estimated time to complete LTS: 0.01 seconds
Total estimated time to complete LMS: 0.01 seconds
Total estimated time to complete LTS: 0.01 seconds
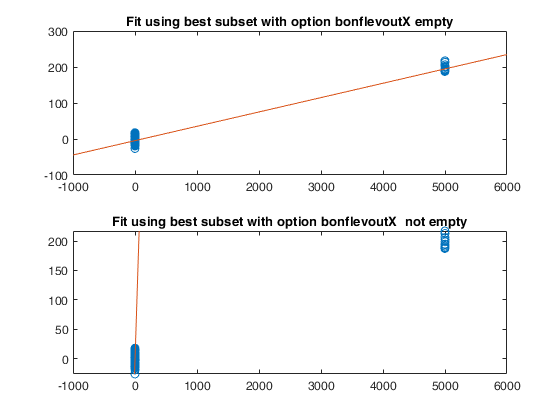
Example of the use of option bonflevoutX.
Example of the use of option bonflevoutX.In this example a set of remote units is added to a cloud of points.
% The purpose of this example is to show that while best LMS using all
% default options contains some of the remote units. In order to make sure
% that the remote units are excluded from the best LMS subset it is
% necessary to use option bonflevoutX.
rng('default')
rng(10000)
n=100;
p=1;
X=randn(n,p);
epsil=10;
beta=ones(p,1);
y=X*beta+randn(n,1)*epsil;
% Add 10 very remote points
add=10;
Xadd=X(1:add,:)+5000;
yadd=y(1:add)+200;
Xall=[X;Xadd];
yall=[y;yadd];
out=LXS(yall,Xall);
subplot(2,1,1)
plot(Xall,yall,'o')
xylim=axis;
line(xylim(1:2),out.beta(1)+out.beta(2)*xylim(1:2))
title('Fit using best subset with option bonflevoutX empty')
subplot(2,1,2)
plot(Xall,yall,'o')
out=LXS(yall,Xall,'bonflevoutX',0.99);
line(xylim(1:2),out.beta(1)+out.beta(2)*xylim(1:2))
ylim(xylim(3:4));
title('Fit using best subset with option bonflevoutX not empty')Total estimated time to complete LMS: 0.01 seconds Total estimated time to complete LMS: 0.05 seconds ------------------------------ Warning: Number of subsets without full rank or excluded because containing remote units in the X space equal to 17.1 %
Input Arguments
Output Arguments
References
Rousseeuw P.J., Leroy A.M. (1987), "Robust regression and outlier detection", Wiley.