MixSim
MixSim generates k clusters in v dimensions with given overlap
Description
Examples
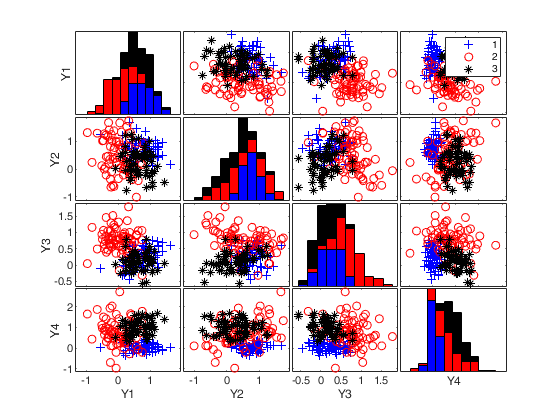
 Generate 3 groups in 4 dimensions.
Generate 3 groups in 4 dimensions.
 Generate 3 groups in 4 dimensions.
Generate 3 groups in 4 dimensions.Use a maximum overlap equal to 0.15.
rng(10,'twister')
out=MixSim(3,4)
n=200;
[X,id]=simdataset(n, out.Pi, out.Mu, out.S);
spmplot(X,id)
out =
struct with fields:
OmegaMap: [3×3 double]
BarOmega: 0.09
MaxOmega: 0.15
StdOmega: 0.05
fail: 0
Pi: [3×1 double]
Mu: [3×4 double]
S: [4×4×3 double]
rcMax: [2×1 double]
ans(:,:,1) =
-1.00 19.06 22.03 25.03
16.02 -1.00 23.03 26.02
17.03 20.03 -1.00 27.02
18.02 21.03 24.03 -1.00
ans(:,:,2) =
-1.00 31.02 34.02 37.02
28.02 -1.00 35.02 38.02
29.02 32.02 -1.00 39.02
30.02 33.02 36.02 -1.00
ans(:,:,3) =
0 43.02 46.01 49.01
40.02 0 47.01 50.01
41.02 44.02 0 51.01
42.02 45.01 48.01 0
Generate 4 groups in 5 dimensions with prefixed average and maximum overlap.
Use average overlap of 0.05 and maximum overlap equal to 0.15.
k=4;
v=5;
BarOmega=0.05;
out=MixSim(4,5,'BarOmega',BarOmega, 'MaxOmega',0.15)
% Check a posteriori the average overlap
disp('Posterior average overlap')
disp((sum(sum(out.OmegaMap))-k)/(0.5*k*(k-1)))
% Check a posteriori the maximum overlap
% Extract elements above the diagonal and sum them with the transpose
% of the elements below the diagonal. The maximum of all these numbers
% must be very close to the required maximum overlap
cand=triu(out.OmegaMap,1)+(tril(out.OmegaMap,-1))'
disp('Posterior average overlap')
max(cand(:))
Related Examples
Example of use of optional input option restrfactor.
In the first case restrfactor is 1.1 and the clusters are roughly homogeneous. In the second case no constraint is imposed on the ratio of maximum and minimum eigevalue among clusters so elliptical shape clusters are allowed. In both cases the same random seed together with the same level of average and maximum overlapping is used
state1=2;
randn('state', state1);
rand('state', state1);
out=MixSim(3,5,'BarOmega',0.1, 'MaxOmega',0.2, 'restrfactor',1.1);
state1=2;
randn('state', state1);
rand('state', state1);
out1=MixSim(3,5,'BarOmega',0.1, 'MaxOmega',0.2);
n=200;
[X,id]=simdataset(n, out.Pi, out.Mu, out.S);
[H,AX,BigAx] = spmplot(X,id,[],'box');
set(gcf,'Name','restrfactor=1.1: almost homogeneous groups')
title(BigAx,'\texttt{restrfactor=1.1}: almost homogeneous groups','fontsize',17,'interpreter','latex');
[X1,id1]=simdataset(n, out1.Pi, out1.Mu, out1.S);
figure;
[H,AX,BigAx] = spmplot(X1,id1,[],'box')
set(gcf,'Name','Heterogeneous groups')
title(BigAx,'\texttt{restrfactor=`''}: heterogeneous groups','fontsize',17,'interpreter','latex')
cascade
Control of average and standard deviation of overlap.
Given an average value of overlap, we explore the differences between imposing a small or a large value of standard deviation of overlap.
clc
close all
rng(10,'twister')
k=4;
v=5;
n=200;
BarOmega=0.10;
StdOmega=0.15;
out=MixSim(k,v,'BarOmega',BarOmega, 'StdOmega',StdOmega,'resN',10, 'Display', 'iter');
[X,id]=simdataset(n, out.Pi, out.Mu, out.S);
rng(10,'twister')
StdOmega1=0.05;
out1=MixSim(k,v,'BarOmega',BarOmega, 'StdOmega',StdOmega1,'resN',10, 'Display', 'iter');
[X1,id1]=simdataset(n, out1.Pi, out1.Mu, out1.S);
disp('Comparison using OmegaMap')
disp('When StdOmega is large in this example groups 3 are 4 do show a strong overlap')
disp('When StdOmega is large in this example groups 1, 2, 3 are quite separate')
disp(out.OmegaMap)
disp('When StdOmega is small the probabilities of overlapping are much more similar')
disp(out1.OmegaMap)
disp('Comparison using interactive scatter plot matrices')
[H,AX,BigAx] = spmplot(X,id,[],'box');
set(gcf,'name',['BarOmega=' num2str(BarOmega) ' StdOmega=' num2str(StdOmega)])
title(BigAx,['BarOmega=' num2str(BarOmega) ' StdOmega=' num2str(StdOmega)])
figure
[H,AX,BigAx] = spmplot(X1,id1,[],'box');
set(gcf,'name',['BarOmega=' num2str(BarOmega) ' StdOmega=' num2str(StdOmega1)])
title(BigAx,['BarOmega=' num2str(BarOmega) ' StdOmega=' num2str(StdOmega1)])
cascade
Input Arguments
k — number of groups (components).
Scalar.
Desired number of groups.
Data Types: int16|int32|int64|single|double
v — number of dimensions (variables).
Scalar.
Desired number of variables.
Data Types: int16|int32|int64|single|double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'BarOmega',0.05
, 'MaxOmega',0.05
, 'StdOmega',0.05
, 'sph',false
, 'hom',false
, 'ecc',0.8
, 'restrfactor',8
, 'PiLow',0.1
, 'int',[0 2]
, 'resN',20
, 'tol',[1e-06 1e-08]
, 'lim',1e6
, 'Display','off'
, 'R_seed',0
BarOmega
—Requested average overlap.scalar.
Value of desired average overlap. The default value is ''
Example: 'BarOmega',0.05
Data Types: double
MaxOmega
—Requested maximum overlap.scalar.
Value of desired maximum overlap. If BarOmega is empty the default value of MaxOmega is 0.15.
Example: 'MaxOmega',0.05
Data Types: double
StdOmega
—Requested std of overlap.scalar.
Value of desired standard deviation of overlap.
Remark1 - The probability of overlapping between two clusters and j, (i \ne j =1, 2, ..., k), called p_{ij}, is defined as the sum of the two misclassification probabilities p_ij=w_{j|i} + w_{i|j} Remark2- it is possible to specify up to two values among BarOmega MaxOmega and StdOmega.
Example: 'StdOmega',0.05
Data Types: double
sph
—Spherical covariances.scalar logical | structure.
Scalar boolean or structure which specifies covariance matrix. When sph is logical value, if: sph=false (default) ==> non-spherical clusters;
sph=true ==> spherical clusters= const*I.
The following options "hom", "ecc" and "restrfactor" have an effect just if sph is a scalar boolean. The default value of sph is false that is non spherical clusters are generated.
If sph is a structure it may contain the following fields.
| Value | Description |
|---|---|
pars |
a 3 letter character in the set: 'VVE','EVE','VVV','EVV','VEE','EEE','VEV','EEV','VVI', 'EVI','VEI','EEI','VII','EII' which specifies the type of Gaussian Parsimonious Clustering Model which needs to be generated. |
exactrestriction |
boolean. If sph.exactrestriction is true the covariance matrices have to be generated with the exact values of the restrictions specified in sph.cdet, sph.shw and sph.shb. For example if sph.pars='VVE' and sph.exactrestriction=true model with varying determinants, varying shape and varying rotation matrix is generated. The max ratio of the determinants is equal to sph.cdet. The maximum ratio between the shape elements in each group is sph.shw. The maximum ratio among the ordered elements across the groups is and sph.shb. On the other hand, if sph.exactrestriction is false and for example sph.pars='VVE' covariance matrices are generated assuming varying determinants, varying shape and equal rotation matrix and with ratio of determinants which satisfy the inequality constraint <= sph.cdet and shape matrices which satisfy the inequality constraints <= sph.shw and <= sph.shb. |
cdet |
scalar which specifies the restriction factor for determinants across groups. If this field is empty or if this field is missing no contraint is imposed among determinants. |
shw |
scalar which specifies the restriction factor for shape matrices within each group. If this field is empty or if this field is missing, no contraint is imposed among the elements of each shape matrix of a particular group. |
shb |
scalar which specifies the restriction factor for shape matrices between each group. If this field is empty or if this field is missing, no contraint is imposed across the elements of each shape matrix between the groups. |
Example: 'sph',false
Data Types: boolean
hom
—Equal Sigmas.scalar logical.
Scalar boolean which specifies heterogeneous or homogeneous clusters. This option has an effect just if previous option sph is a scalar boolean.
hom=false (default) ==> heterogeneous;
hom=true ==> homogeneous \Sigma_1 = ... = \Sigma_k
Example: 'hom',false
Data Types: boolean
ecc
—maximum eccentricity.scalar.
Scalar in the interval (0, 1] which defines maximum eccentricity.
For example, if ecc=0.9 (default value), we require for each group that sqrt(1 - minL / maxL) <= 0.9 where minL and maxL are respectively the min and max eigenvalue of the cov matrix of a particular group. This option has an effect just if previous option sph is a scalar boolean.
Example: 'ecc',0.8
Data Types: double
restrfactor
—eigenvalue restriction factor.scalar.
Scalar in the interval [1 \infty] which specifies the maximum ratio to allow between the largest eigenvalue and the smallest eigenvalue of the k covariance matrices which are generated. The default value is ''. More in details if for example restrfactor=10 after generating the covariance matrices we check that the ratio \frac{ \max_{l=1, \ldots, v} \max_{j=1, \ldots, k} \lambda_l(\hat \Sigma_j)}{ \min_{l=1, \ldots, v} \min_{j=1, \ldots, k} \lambda_l(\hat \Sigma_j)}.
between the largest eigenvalue of the k cov matrices and the smallest eigenvalue of the k cov matrices is not larger than restrfactor. In order to apply this restriction (which is typical of tclust.m) we call routine restreigen.
This option has an effect just if previous option sph is a scalar boolean.
Example: 'restrfactor',8
Data Types: double
PiLow
—Smallest mixing proportion.scalar.
Value of the smallest mixing proportion (if 'PiLow' is not reachable with respect to k, equal proportions are taken; PiLow = 1.0 implies equal proportions by default).
PiLow must be a number in the interval (0 1]. Default value 0.
Example: 'PiLow',0.1
Data Types: double
int
—Simulation interval of mean vectors.vector of length 2.
Mean vectors are simulated uniformly on a hypercube with sides specified by int = [lower.bound, upper.bound].
The default value of int is [0 1].
Example: 'int',[0 2]
Data Types: double
resN
—number of simulations.scalar.
Maximum number of mixture resimulations to find a similation setting with prespecified level of overlapping.
The default value of resN is 100
Example: 'resN',20
Data Types: double
tol
—Tolerances.vector of length 2.
tol(1) (which will be called tolmap) specifies the tolerance between the requested and empirical misclassification probabilities (default is 1e-06) tol(2) (which will be called tolnxc2) specifies the tolerance to use in routine ncx2mixtcdf (which computes cdf of linear combinations of non central chi2 distributions).
The default value of tol(2) 1e-06.
Example: 'tol',[1e-06 1e-08]
Data Types: double
lim
—Precision in the calculation of probabilities of overlapping.scalar.
Maximum number of integration terms to use inside routine ncx2mixtcdf. Default is 1e06.
REMARK - Optional parameters tolncx2=tol(2) and lim will be used by function ncx2mixtcdf which computes the cdf of a linear combination of non central chi2 r.v.. This is the probability of misclassification
Example: 'lim',1e6
Data Types: double
Display
—Level of display.character.
'off' displays no output;
'notify' (default) displays output if requested overlap cannot be reached in a particular simulation 'iter' displays output at each iteration of each simulation
Example: 'Display','off'
Data Types: character
R_seed
—use random numbers from R.scalar.
If scalar > 0 for the seed to be used to generate random numbers in a R instance. This is used to check consistency of the results obtained with the R package MixSim. See file Connect_Matlab_with_R_HELP to know how to connect MATLAB with R. This option requires the installation of the R-(D)COM Interface. Default is 0, i.e. random numbers are generated by matlab.
Example: 'R_seed',0
Data Types: double
Output Arguments
out — description
Structure
Structure which contains the following fields
| Value | Description |
|---|---|
Pi |
vector of length k containing mixing proportions. sum(out.Pi)=1 |
Mu |
k-by-v matrix consisting of components' mean vectors Each row of this matrix is a centroid of a group |
S |
v-by-v-by-k array containing covariances for the k groups |
OmegaMap |
matrix of misclassification probabilities (k-by-k); OmegaMap(i,j) = w_{j|i} is the probability that X coming from the i-th component (group) is classified to the j-th component. |
BarOmega |
scalar. Value of average overlap. BarOmega is computed as (sum(sum(OmegaMap))-k)/(0.5*k(k-1)) |
MaxOmega |
scalar. Value of maximum overlap. MaxOmega is the maximum of OmegaMap(i,j)+OmegaMap(j,i) (i ~= j)=1, 2, ..., k. In other words MaxOmega= OmegaMap(rcMax(1),rcMax(2))+OmegaMap(rcMax(2),rcMax(1)) |
StdOmega |
scalar. Value of standard deviation (std) of overlap. StdOmega is the standard deviation of k*(k-1)/2 probabilities of overlapping |
rcMax |
vector of length 2. It containes the row and column numbers associated with the pair of components producing maximum overlap 'MaxOmega' |
fail |
scalar, flag value. 0 represents successful mixture generation, 1 represents failure. |
More About
Additional Details
MixSim(k,v) generates k groups in v dimensions. It is possible to control the average and maximum or standard deviation of overlapping.
Given two generic clusters i and j with i \ne j =1, ..., k, indexed by \phi(x; \mu_i,\Sigma_i) and \phi(x; \mu_j,\Sigma_j) with probabilities of occurrence \pi_i and \pi_j, the misclassification probability with respect to cluster i (that is conditionally on x belonging to cluster i, which is called w_{j|i}) is defined as Pr[ \pi_i \phi(x;\mu_i,\Sigma_i) < \pi_j \phi(x;\mu_j,\Sigma_j)].
The matrix containing the misclassification probabilities w_{j|i} is called OmegaMap The probability of overlapping between groups i and j is given by:
w_{j|i} + w_{i|j} \qquad i,j=1,2, ..., kThe diagonal elements of OmegaMap are equal to 1.
The average overlap (which in the code is called below BarOmega) is defined as the sum of the off diagonal elements of OmegaMap (matrix of misclassification probabilities) divided by 0.5*k*(k-1) The maximum overlap (which in the code is called MaxOmega) is defined as \max(w_{j|i} + w_{i|j}), i \ne j=1,2, ..., k.
The probability of misclassification w_{j|i} is nothing but the cdf of a linear combination of non central \chi^2 distributions with 1 degree of freedom + a linear combination of N(0,1) evaluated in a point c. The coefficients of the linear combinations of non central \chi^2 and N(0,1) depend on the eigenvalues and eigenvectors of matrix \Sigma_{j|i} = \Sigma^{0.5}_i \Sigma^{-1}_j \Sigma^{0.5}_i.
Point c depends on the same eigenvalues and eigenvectors of matrix \Sigma_{j|i}, the mixing proportions \pi_i and \pi_j and the determinants |\Sigma_i| and |\Sigma_j|.
This probability is computed using routine ncx2mixtcdf
References
Maitra, R. and Melnykov, V. (2010), Simulating data to study performance of finite mixture modeling and clustering algorithms, "The Journal of Computational and Graphical Statistics", Vol. 19, pp. 354-376. [to refer to this publication we will use "MM2010 JCGS"]
Melnykov, V., Chen, W.-C. and Maitra, R. (2012), MixSim: An R Package for Simulating Data to Study Performance of Clustering Algorithms, "Journal of Statistical Software", Vol. 51, pp. 1-25.
Davies, R. (1980), The distribution of a linear combination of chi-square random variables, "Applied Statistics", Vol. 29, pp. 323-333.
Garcia-Escudero, L.A., Gordaliza, A., Matran, C. and Mayo-Iscar, A. (2008), A General Trimming Approach to Robust Cluster Analysis. Annals of Statistics, Vol. 36, 1324-1345.
Riani, M., Cerioli, A., Perrotta, D. and Torti, F. (2015), Simulating mixtures of multivariate data with fixed cluster overlap in FSDA, "Advances in data analysis and classification", Vol. 9, pp. 461-481.
Parlett, B.N. and Reinsch, C. (1971), Balancing a Matrix for Calculation of Eigenvalues and Eigenvectors, in Bauer, F.L. Eds, "Handbook for Automatic Computation", Vol. 2, pp. 315-326, Springer.
See Also
tkmeans
|
tclust
|
tclustreg
|
lga
|
rlga
|
ncx2mixtcdf
|
restreigen