corrOrdinal
corrOrdinal measures strength of association between two ordered categorical variables.
Description
corrOrdinal computes Goodman-Kruskal's , \tau_a, \tau_b, \tau_c of Kendall and d_{y|x} of Somers.
All these indexes measure the correlation among two ordered qualitative variables and go between -1 and 1. The sign of the coefficient indicates the direction of the relationship, and its absolute value indicates the strength, with larger absolute values indicating stronger relationships. Values close to an absolute value of 1 indicate a strong relationship between the two variables. Values close to 0 indicate little or no relationship. More in detail: \gamma is a symmetric measure of association.
Kendall's \tau_a is a symmetric measure of association that does not take ties into account. Ties happen when both members of the data pair have the same value.
Kendall's \tau_b is a symmetric measure of association which takes ties into account. Even if \tau_b ranges from -1 to 1, a value of -1 or +1 can be obtained only from square tables.
\tau_c (also called Stuart-Kendall \tau_c) is a symmetric measure of association which makes an adjustment for table size in addition to a correction for ties. Even if \tau_c ranges from -1 to 1, a value of -1 or +1 can be obtained only from square tables.
Somers' d is an asymmetric extension of \tau_b in that it uses a correction only for pairs that are tied on the independent variable (which in this implementation it is assumed to be on the rows of the contingency table).
Additional details about these indexes can be found in the "More About" section of this document.
Compare calculation of tau-b with that which comes from
Matlab function corr.out
=corrOrdinal(N,
Name, Value)
Examples
Related Examples
Input Arguments
Output Arguments
More About
References
Agresti, A. (2002), "Categorical Data Analysis", John Wiley & Sons. [pp.
57-59]
Agresti, A. (2010), "Analysis of Ordinal Categorical Data", Second Edition, Wiley, New York, pp. 194-195.
Goktas, A. and Oznur, I. (2011), A comparision of the most commonly used measures of association for doubly ordered square contingency tables via simulation, "Metodoloski zvezki", Vol. 8, pp. 17-37,
Goodman, L.A. and Kruskal, W.H. (1954), Measures of association for cross classifications, "Journal of the American Statistical Association", Vol. 49, pp. 732-764.
Goodman, L.A. and Kruskal, W.H. (1959), Measures of association for cross classifications II: Further Discussion and References, "Journal of the American Statistical Association", Vol. 54, pp. 123-163.
Goodman, L.A. and Kruskal, W.H. (1963), Measures of association for cross classifications III: Approximate Sampling Theory, "Journal of the American Statistical Association", Vol. 58, pp. 310-364.
Goodman, L.A. and Kruskal, W.H. (1972), Measures of association for cross classifications IV: Simplification of Asymptotic Variances, "Journal of the American Statistical Association", Vol. 67, pp. 415-421.
Hollander, M, Wolfe, D.A., Chicken, E. (2014), "Nonparametric Statistical Methods", Third edition, Wiley,
Liebetrau, A.M. (1983), "Measures of Association", Sage University Papers Series on Quantitative Applications in the Social Sciences, 07-004, Newbury Park, CA: Sage. [pp. 49-56]
SAS documentation (2009), See http://support.sas.com/documentation/cdl/en/statugfreq/63124/PDF/default/statugfreq.pdf, pp. 1738-1740.
Morton, B.B. and Benedetti, J.K. (1977), Sampling Behavior of Tests for Correlation in Two-Way Contingency Tables, "Journal of the American Statistical Association", Vol. 72, pp. 309-315.
Simon, G. (1978), Alternative analysis for the singly ordered contingency table, "Journal of the American Statistical Association", Vol. 69, pp. 971-976.
Acknowledgements
This file was inspired by Trujillo-Ortiz, A. and R. Hernandez-Walls.
gkgammatst: Goodman-Kruskal's gamma test. URL address http://www.mathworks.com/matlabcentral/fileexchange/42645-gkgammatst
See Also
crosstab
|
rcontFS
|
CressieRead
|
corr
|
corrNominal

|
corrNominal |
corrpdf |
 |
|
|
Functions |
|
• The developers of the toolbox • The forward search group • Terms of Use • Acknowledgments
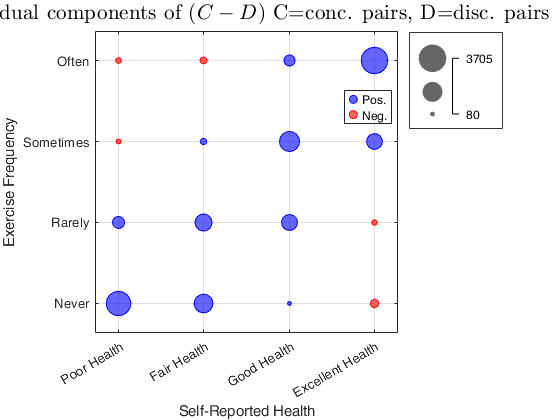
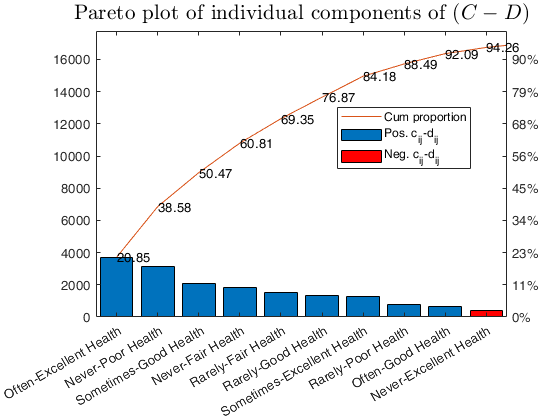
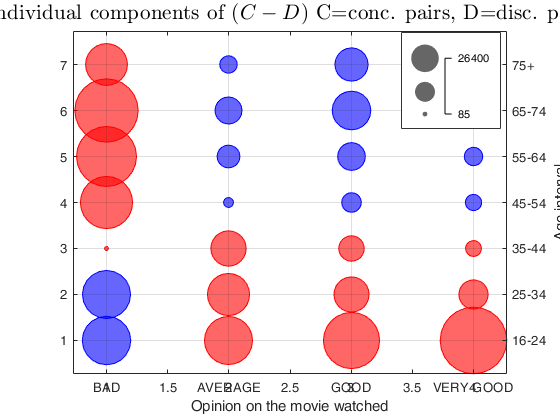
 corrOrdinal with all the default options.
corrOrdinal with all the default options.