mve

mve computes Minimum volume ellipsoid

expand all in page

Syntax

Description

example

RAW =mve(Y) mve with all default options.

example

RAW =mve(Y, Name, Value) mve with optional arguments.

example

[RAW, REW] =mve(___) mve monitoring the reweighted estimates.

example

[RAW, REW, varargout] =mve(___) mve monitoring the extracted subsamples.

Examples

expand all

  • mve with all default options.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
RAW=mve(Ycont);

  • mve with optional arguments.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
RAW=mve(Ycont,'plots',1);
    Warning: Using 'state' to set RANDN's internal state causes RAND, RANDI, and
RANDN to use legacy random number generators.  This syntax is not recommended.
See <a href="matlab:helpview([docroot '\techdoc\math\math.map'],'update_random_number_generator')">Replace Discouraged Syntaxes of rand and randn</a> to use RNG to replace the
old syntax. 
Total estimated time to complete MVE:  0.17 seconds
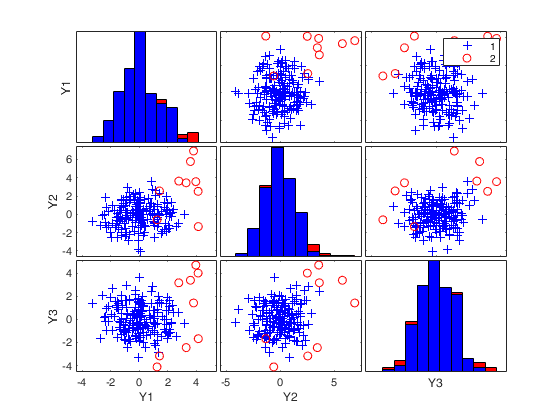
    Click here for the graphical output of this example (link to Ro.S.A. website).

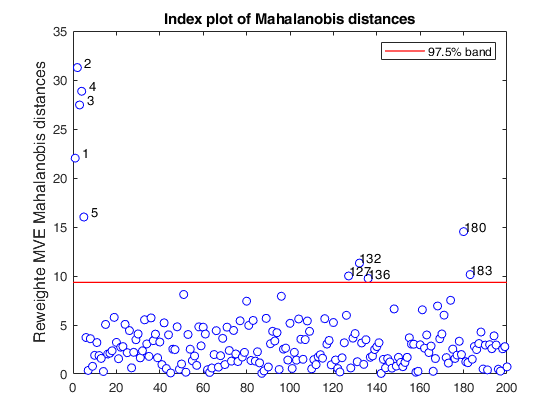
  • mve monitoring the reweighted estimates.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
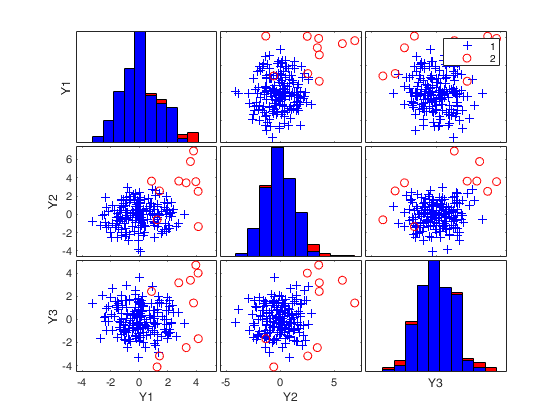
[RAW,REW]=mve(Ycont);

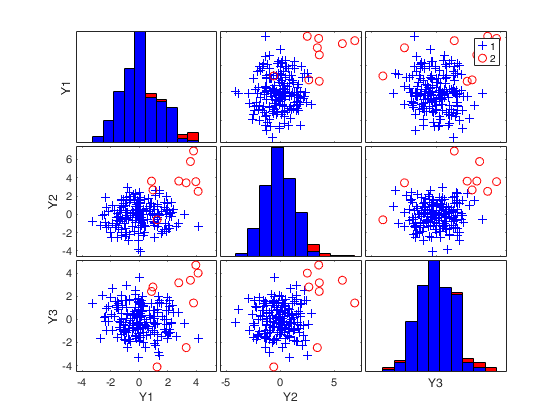
  • mve monitoring the extracted subsamples.

    • n=200;
v=3;
randn('state', 123456);
Y=randn(n,v);
% Contaminated data
Ycont=Y;
Ycont(1:5,:)=Ycont(1:5,:)+3;
[RAW,REW,C]=mve(Ycont);
    Total estimated time to complete MVE:  0.25 seconds

    Input Arguments

    expand all

    Y — Input data. Matrix.

    n x v data matrix; n observations and v variables. Rows of Y represent observations, and columns represent variables.

    Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    Data Types: single|double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'bdp',1/4 , 'nsamp',10000 , 'refsteps',0 , 'reftol',1e-8 , 'conflev',0.99 , 'nocheck',1 , 'plots',1 , 'msg',1 , 'ysaveRAW',1 , 'ysaveREW',1

    bdp —Breakdown point.scalar.

    Number between 0 and 0.5 which specifies the break down point. The default value is 0.5.

    Example: 'bdp',1/4

    Data Types: double

    nsamp —Number of subsamples.scalar.

    Number of subsamples of size v+1 which have to be extracted (if not given, default = 500).

    Example: 'nsamp',10000

    Data Types: double

    refsteps —Number of refining iterations.scalar.

    Number of refining iterationsin each subsample (default = 3).

    refsteps = 0 means "raw-subsampling" without iterations.

    Example: 'refsteps',0

    Data Types: single | double

    reftol —Tolerance for the refining steps.scalar.

    Default value of tolerance for the refining steps.

    The default value is 1e-6;

    Example: 'reftol',1e-8

    Data Types: single | double

    conflev —Confidence level Scalar.number between 0 and 1 containing confidence level which is used to declare units as outliers.

    Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).

    Default value is 0.975

    Example: 'conflev',0.99

    Data Types: double

    nocheck —No check on input data.scalar.

    If nocheck is equal to 1 no check is performed on matrix Y. As default nocheck=0.

    Example: 'nocheck',1

    Data Types: double

    plots —Plot on the screen.scalar | structure.

    If plots is a structure or scalar equal to 1, generates: (1) a plot of Mahalanobis distances against index number. The confidence level used to draw the confidence bands for the MD is given by the input option conflev. If conflev is not specified a nominal 0.975 confidence interval will be used.

    (2) a scatter plot matrix with the outliers highlighted.

    If plots is a structure it may contain the following fields

    Value Description
    labeladd

    if this option is '1', the outliers in the spm are labelled with their unit row index. The default value is labeladd='', i.e. no label is added.
    nameY

    cell array of strings containing the labels of the variables. As default value, the labels which are added are Y1, ...Yv.

    Example: 'plots',1

    Data Types: double or structure

    msg —Level of display.scalar.

    Display or not messages on the screen. If msg==1 (default) messages are displayed on the screen about estimated time to compute the final estimator else no message is displayed on the screen.

    Example: 'msg',1

    Data Types: double

    ysaveRAW —save input matrix.scalar.

    Scalar that is set to 1 to request that the data matrix Y is saved into the output structure RAW. This feature is meant at simplifying the use of function malindexplot. Default is 0, i.e. no saving is done.

    Example: 'ysaveRAW',1

    Data Types: double

    ysaveREW —save input matrix.scalar.

    Scalar that is set to 1 to request that the data matrix Y is saved into the output structure REW. This feature is meant at simplifying the use of function malindexplot.

    Default is 0, i.e. no saving is done.

    Example: 'ysaveREW',1

    Data Types: double

    Output Arguments

    expand all

    RAW — description Structure

    Structure which contains the following fields

    Value Description
    loc

    1 x v vector containing raw MCD location of the data
    cov

    robust MCD estimate of covariance matrix. It is the raw MCD covariance matrix (multiplied by a finite sample correction factor and an asymptotic consistency factor).
    cor

    The raw MVE correlation matrix
    obj

    The value of the objective function which has been minimized.
    bs

    (v+1) x 1 vector containing the units forming best subset associated with MVE estimate of location.
    md

    n x 1 vector containing the estimates of the robust Mahalanobis distances (in squared units). This vector contains the distances of each observation from the raw MCD location of the data, relative to the raw MCD scatter matrix RAW.cov
    outliers

    A vector containing the list of the units declared as outliers using confidence level specified in input scalar conflev
    conflev

    Confidence level that was used to declare outliers
    singsub

    Number of subsets without full rank. Notice that out.singsub > 0.1*(number of subsamples) produces a warning
    weights

    n x 1 vector containing the estimates of the weights.

    These weights determine which are the h observations are used to compute the final MVE estimates.
    h

    number of observations which have determined MVE.
    Y

    Data matrix Y. The field is present only if option ysaveRAW is set to 1.
    class

    'mve'.

    REW — description Structure

    Structure which contains the following fields:

    Value Description
    loc

    The robust location of the data, obtained after reweighting, if the RAW.cov is not singular. Otherwise the raw MVE center is given here.
    cov

    The robust covariance matrix, obtained after reweighting and multiplying with a finite sample correction factor and an asymptotic consistency factor, if the raw MVE is not singular. Otherwise the raw MVE covariance matrix is given here.
    cor

    The robust correlation matrix, obtained after reweighting
    md

    The distance of each observation to the final, reweighted MVE center of the data, relative to the reweighted MVE scatter of the data. These distances allow us to easily identify the outliers. If the reweighted MVE is singular, RAW.md is given here.
    outliers

    A vector containing the list of the units declared as outliers after reweighting.
    Y

    Data matrix Y. The field is present only if option ysaveRAW is set to 1.
    class

    'mver';

    varargout —Indices of the subsamples extracted for computing the estimate. C : matrix of size nsamp-by-v

    More About

    expand all

    Additional Details

    For each subset $J$ of $v+1$ observations $\mu_J$ and $C_J$ are the centroid and the covariance matrix based on subset $J$.

    Rousseeuw and Leroy (RL) (eq. 1.25 chapter 7, p. 259) write the objective function for subset $J$ as

    \[ RL_J=\left( med_{i=1, ..., n} \sqrt{ (y_i -\mu_J)' C_J^{-1} (y_i -\mu_J) } \right)^v \sqrt|C_J| \] Maronna Martin and Yohai (MMY), eq. (6.57), define $\Sigma_J = C_j / |C_j|^{1/v}$ and write the objective function for subset $J$ as \[ MMY_J = \hat \sigma \left( (y_i -\mu_J)' \Sigma_J^{-1} (y_i -\mu_J) \right) |C_J|^{1/v} = \hat \sigma \left( (y_i -\mu_J)' C_J^{-1} (y_i -\mu_J) \right) |C_J|^{1/v} \]

    where $\hat \sigma \left( (y_i -\mu_J)' C_J^{-1} (y_i -\mu_J) \right) = med_{i=1, ..., n}(y_i -\mu_J)' C_J^{-1} (y_i -\mu_J)$.

    Note that $MMY_J= (RL)^{2/v}$.

    To RAW.cov a consistency factor has been applied which is based on chi2inv(1-bdp,v). On the other hand to REW.cov the usual asymptotic consistency factor is applied. In this case we have used the empirical percentage of trimming that is the ratio hemp/n where hemp is the number of units which had a MD smaller than the cutoff level determined by thresh=chi2inv(conflev,v); MD are computed using RAW.loc and RAW.cov.

    The mve method is intended for continuous variables, and assumes that the number of observations n is at least 5 times the number of variables v.

    References

    Rousseeuw, P.J. (1984), Least Median of Squares Regression, "Journal of the American Statistical Association", Vol. 79, pp. 871-881.

    Rousseeuw, P.J. and Leroy A.M. (1987), Robust regression and outlier detection, Wiley New York.

    Acknowledgements

    This function follows the lines of MATLAB/R code developed during the years by many authors.

    For more details see the R library robustbase http://robustbase.r-forge.r-project.org/ The core of these routines, e.g. the resampling approach, however, has been completely redesigned, with considerable increase of the computational performance.

    See Also

    This page has been automatically generated by our routine publishFS