tclustICsol
tclustICsol extracts a set of best relevant solutions
Description
tclustICsol takes as input the output of function tclustIC or tclustICreg (that is a series of matrices which contain the values of the information criteria BIC/ICL/CLA for different values of and c (or \alpha) and extracts the first best solutions. Two solutions are considered equivalent if the value of the adjusted Rand index (or the adjusted Fowlkes and Mallows index) is above a certain threshold.
For each tentative solution the program checks the adjacent values of c (\alpha) for which the solution is stable. A matrix with adjusted Rand indexes is given for the extracted solutions.
Simulated data: compare first 3 best solutions using MIXMIX and CLACLA.out
=tclustICsol(IC,
Name, Value)
Examples
 Plot of first two best solutions for Geyser data.
Plot of first two best solutions for Geyser data.
 Plot of first two best solutions for Geyser data.
Plot of first two best solutions for Geyser data.
Y=load('geyser2.txt');
outIC=tclustIC(Y,'cleanpool',false,'plots',0,'alpha',0.1);
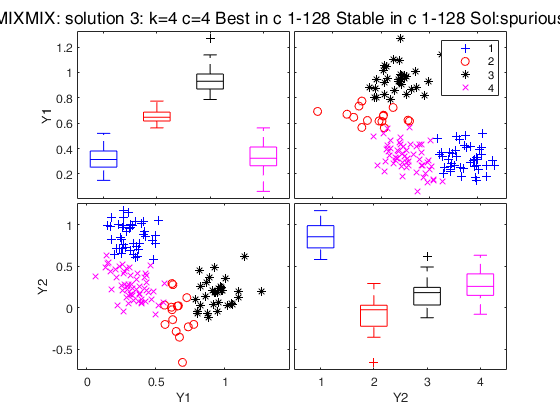
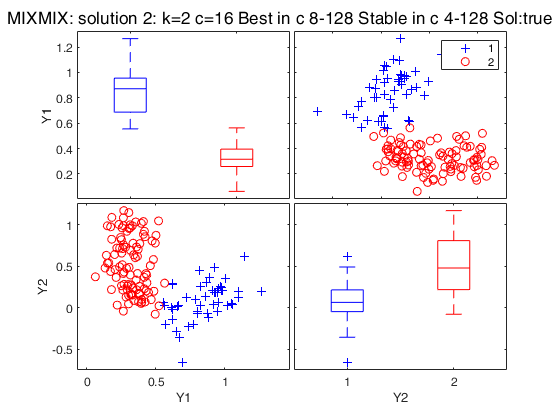
% Plot first two best solutions using as Information criterion MIXMIX
disp('Best solutions using MIXMIX')
[out]=tclustICsol(outIC,'whichIC','MIXMIX','plots',1,'NumberOfBestSolutions',2);
disp(out.MIXMIXbs)
k=1
k=2
k=3
k=4
k=5
Best solutions using MIXMIX
{[3]} {[ 4]} {7×1 double} {[ 1]} {'true' }
{[4]} {[32]} {8×1 double} {0×0 double} {'spurious'}
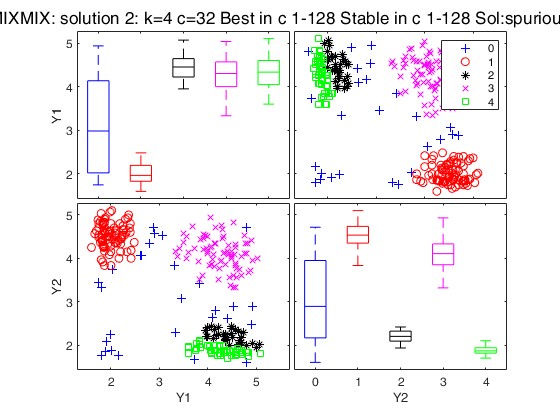
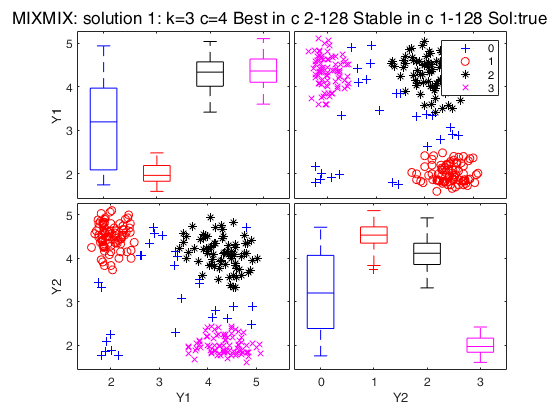

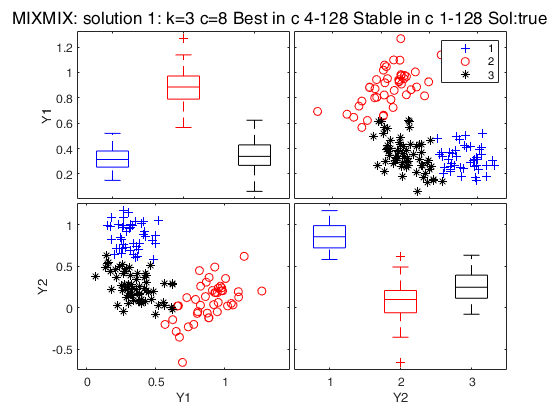
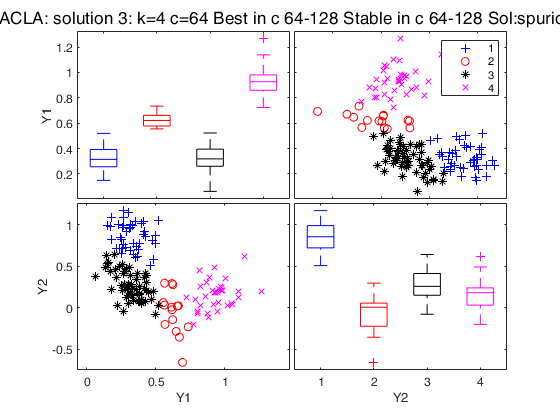
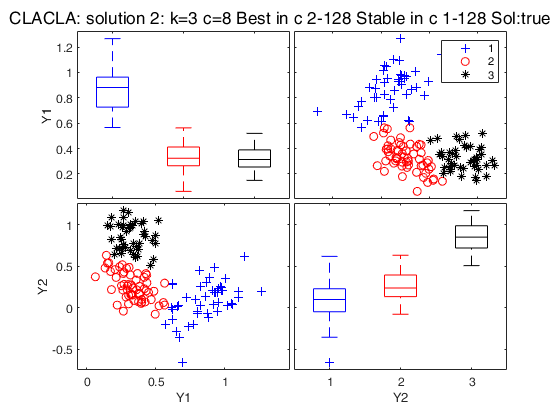
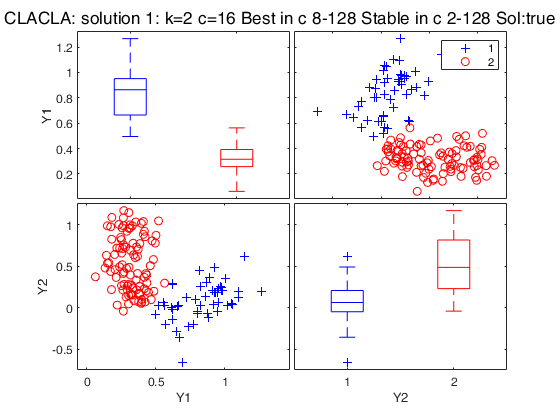
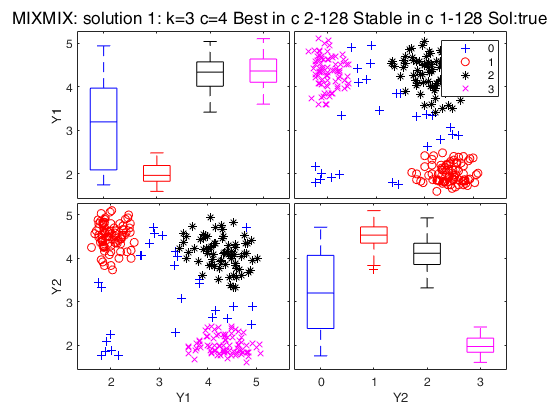
 Simulated data: compare first 3 best solutions using MIXMIX and CLACLA.
Simulated data: compare first 3 best solutions using MIXMIX and CLACLA.
 Simulated data: compare first 3 best solutions using MIXMIX and CLACLA.
Simulated data: compare first 3 best solutions using MIXMIX and CLACLA.Data generation
restrfact=5;
rng('default') % Reinitialize the random number generator to its startup configuration
rng(20000);
ktrue=3;
% n = number of observations
n=150;
% v= number of dimensions
v=2;
% Imposed average overlap
BarOmega=0.04;
outMS=MixSim(ktrue,v,'BarOmega',BarOmega, 'restrfactor',restrfact);
% data generation given centroids and cov matrices
[Y,id]=simdataset(n, outMS.Pi, outMS.Mu, outMS.S);
% Computation of information criterion
outIC=tclustIC(Y,'cleanpool',false,'plots',0,'nsamp',200);
% Plot first 3 best solutions using as Information criterion MIXMIX
disp('Best 3 solutions using MIXMIX')
[outMIXMIX]=tclustICsol(outIC,'whichIC','MIXMIX','plots',1,'NumberOfBestSolutions',3);
disp(outMIXMIX.MIXMIXbs)
disp('Best 3 solutions using CLACLA')
[outCLACLA]=tclustICsol(outIC,'whichIC','CLACLA','plots',1,'NumberOfBestSolutions',3);
disp(outCLACLA.CLACLAbs)
k=1
k=2
k=3
k=4
k=5
Best 3 solutions using MIXMIX
{[3]} {[ 8]} {6×1 double} {2×1 double} {'true' }
{[2]} {[16]} {5×1 double} {[ 4]} {'true' }
{[4]} {[ 4]} {8×1 double} {0×0 double} {'spurious'}
Best 3 solutions using CLACLA
{[2]} {[16]} {5×1 double} {2×1 double} {'true' }
{[3]} {[ 8]} {7×1 double} {[ 1]} {'true' }
{[4]} {[64]} {2×1 double} {0×1 double} {'spurious'}


Related Examples
An example with input option kk.
Y=load('geyser2.txt');
out=tclustIC(Y,'cleanpool',false,'plots',1,'alpha',0.1,'whichIC','CLACLA','kk',[2 3 4 6])
[outCLACLCA]=tclustICsol(out,'whichIC','CLACLA','plots',1,'NumberOfBestSolutions',3);
Comparison between the use of Rand index and FM index.
Y=load('geyser2.txt');
out=tclustIC(Y,'cleanpool',false,'plots',1,'alpha',0.1,'whichIC','CLACLA');
[outCLACLCA]=tclustICsol(out,'whichIC','CLACLA','plots',0,'NumberOfBestSolutions',5,'Rand',1);
disp('Matrix of adjusted Rand indexes among the first 5 best solutions')
disp(outCLACLCA.CLACLAbsari)
[outCLACLCA]=tclustICsol(out,'whichIC','CLACLA','plots',0,'NumberOfBestSolutions',5,'Rand',0);
disp('Matrix of adjusted Fowlkes and Mallows indexes among the first 5 best solutions')
disp(outCLACLCA.CLACLAbsari)
Input Arguments
IC — Information criterion to use.
Structure.
It contains the following fields.
| Value | Description |
|---|---|
CLACLA |
matrix of size length(kk)-by-length(cc) or of size length(kk)-by-length(alpha) containinig the values of the penalized classification likelihood (CLA). This field is linked with out.IDXCLA. |
IDXCLA |
cell of size length(kk)-by-length(cc) or of size length(kk)-by-length(alpha). Each element of the cell is a vector of length n containinig the assignment of each unit using the classification model. Remark: fields CLACLA and IDXCLA are linked together. CLACLA and IDXCLA are compulsory just if optional input argument 'whichIC' is 'CLACLA' or 'ALL'. |
MIXMIX |
matrix of size length(kk)-by-length(cc) or of size length(kk)-by-length(alpha) containinig the value of the penalized mixture likelihood (BIC). This field is linked with out.IDXMIX. |
MIXCLA |
matrix of size length(kk)-times length(cc) or of size length(kk)-by-length(alpha) containinig the value of the ICL. This field is linked with out.IDXMIX. |
IDXMIX |
cell of size length(kk)-times length(cc) or of size length(kk)-by-length(alpha). Each element of the cell is a vector of length n containinig the assignment of each unit using the mixture model. Remark 1: fields MIXMIX and IDXMIX are linked together. MIXMIX and IDXMIX are compulsory just if optional input argument 'whichIC' is 'CLACLA' or 'ALL'. Remark 2: fields MIXCLA and IDXMIX are linked together. MIXCLA and IDXMIX are compulsory just if optional input argument 'whichIC' is 'MIXCLA' or 'ALL'. |
kk |
vector containing the values of k (number of components) which have been considered. |
cc |
vector containing the values of c (values of the restriction factor) which have been considered. |
alpha |
vector containing the values of c (values of the trimming level) which have been considered. |
Y |
original n-times-v data matrix on which the IC (Information criterion) has been computed. This input option is present only if IC comes from tclustIC. |
y |
original n-times-1 regression response on which the IC (Information criterion). This input option is present only if IC comes from tclustregIC. |
X |
original n-times-p matrix of explanatory varaibles on which the IC (Information criterion). This input option is present only if IC comes from tclustregIC. |
Data Types: struct
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'NumberOfBestSolutions',5
, 'ThreshRandIndex',0.8
, 'whichIC','ALL'
, 'plots',1
, 'SpuriousSolutions',false
, 'msg',1
, 'Rand',1
NumberOfBestSolutions
—number of solutions to consider.scalar integer greater than 0.
Number of best solutions to extract from BIC/ICL matrix. The default value of NumberOfBestSolutions is 5
Example: 'NumberOfBestSolutions',5
Data Types: int16 | int32 | single | double
ThreshRandIndex
—threshold to identify spurious solutions.positive scalar between 0 and 1.
Scalar which specifies the threshold of the adjusted Rnd index to use to consider two solutions as equivalent. The default value of ThreshRandIndex is 0.7
Example: 'ThreshRandIndex',0.8
Data Types: single | double
whichIC
—character which specifies the information criterion to use
to extract best solutions.character.
Possible values for whichIC are: 'CLACLA' = in this case best solutions are referred to the classification likelihood.
'MIXMIX' = in this case in this case best solutions are referred to the mixture likelihood (BIC).
'MIXCLA' = in this case in this case best solutions are referred to ICL.
'ALL' = in this case best solutions both three solutions using classification and mixture likelihood are produced. In output structure out all the three matrices out.MIXMIXbs, out.CLACLAbs and out.MIXCLAbs are given.
The default value of 'whichIC' is 'ALL'
Example: 'whichIC','ALL'
Data Types: character
plots
—plots of best solutions on the screen.scalar.
It specifies whether to plot on the screen the best solutions which have been found.
Example: 'plots',1
Data Types: single | double
SpuriousSolutions
—Include or nor spurious solutions in the plot.boolean.
As default spurios solutions are shown in the plot.
Example: 'SpuriousSolutions',false
Data Types: single | double
msg
—Message on the screen.scalar.
Scalar which controls whether to display or not messages about code execution.
The default value of msg is 0, that is no message is displayed on the screen.
Example: 'msg',1
Data Types: single | double
Rand
—Index to use to compare partitions.scalar.
If Rand =1 (default) the adjusted Rand index is used, else the adjusted Fowlkes and Mallows index is used
Example: 'Rand',1
Data Types: single | double
Output Arguments
out — description
Structure
Structure which contains the following fields:
| Value | Description |
|---|---|
MIXMIXbs |
cell of size NumberOfBestSolutions-times-5 which contains the details of the best solutions for MIXMIX (BIC). Each row refers to a solution. The information which is stored in the columns is as follows. 1st col = scalar, value of k for which solution takes place; 2nd col = scalar, value of c for which solution takes place; 3rd col = row vector of length d which contains the values of c for which the solution is uniformly better. 4th col = row vector of length d+r which contains the values of c for which the solution is considered stable (i.e. for which the value of the adjusted Rand index (or the adjusted Fowlkes and Mallows index) does not go below the threshold defined in input option ThreshRandIndex). 5th col = string which contains 'true' or 'spurious'. The solution is labelled spurious if the value of the adjusted Rand index with the previous solutions is greater than ThreshRandIndex. Remark: field out.MIXMIXbs is present only if input option 'whichIC' is 'ALL' or 'whichIC' is 'MIXMIX'. |
MIXMIXbsari |
matrix of adjusted Rand indexes (or Fowlkes and Mallows indexes) associated with the best solutions for MIXMIX. Matrix of size NumberOfBestSolutions-times-NumberOfBestSolutions whose i,j-th entry contains the adjusted Rand index between classification produced by solution i and solution j, i,j=1, 2, \ldots, NumberOfBestSolutions. Remark: field out.MIXMIXbsari is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXMIX'. |
ARIMIX |
Matrix of adjusted Rand indexes between two consecutive value of c. Matrix of size k-by-length(cc)-1. The first column contains the ARI indexes between with cc(2) and cc(1) given k. The second column contains the the ARI indexes between cc(3) and cc(2) given k. This output is also present in table format (see below) Remark: field ARIMIX is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXMIX' or 'MIXLCA' |
ARIMIXtable |
Table with the same meaning of matrix ARIMIX above. A Matlab table has also been been given to faciliate the interpretation of the rows and columns. The Rownames of this table correspond to the values of k which are used and the colNames of this table contain in a dynamic way the two values of c which are considered. For example if the first two values of c are c=3 and c=7, the first column name of this table is c3_v_c7 to denote that the entry of this column are the ARI indexes between c=3 and c=7 Remark: field ARIMIXtable is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXMIX' or 'MIXLCA' |
MIXCLAbs |
this output has the same structure as out.MIXMIXbs but it is referred to MIXCLA. Remark: field out.MIXCLAbs is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXCLA'. |
MIXCLAbsari |
this output has the same structure as out.MIXMIXbs but it is referred to MIXCLA. Remark: field out.MIXCLAbsari is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXCLA'. |
CLACLAbs |
this output has the same structure as out.MIXMIXbs but it is referred to CLACLA. Remark: field out.CLACLAbs is present only if 'whichIC' is 'ALL' or 'whichIC' is 'CLACLA'. |
CLACLAbsari |
this output has the same structure as out.MIXMIXbs but it is referred to CLACLA. Remark: field out.MIXCLAbsari is present only if 'whichIC' is 'ALL' or 'whichIC' is 'CLACLA' |
ARICLA |
Matrix of adjusted Rand indexes between two consecutive value of c. Matrix of size k-by-length(cc)-1. The first column contains the ARI indexes between with cc(2) and cc(1) given k. The second column contains the the ARI indexes between cc(3) and cc(2) given k. This output is also present in table format (see below) Remark: field ARICLA is present only if 'whichIC' is 'ALL' or 'whichIC' is 'CLACLA' |
ARICLAtable |
Table with the same meaning of matrixo CLACLAari above. A Matlab table has also been been given to faciliate the interpretation of the rows and columns. The Rownames of this table correspond to the values of k which are used and the colNames of this table contain in a dynamic way the two adjacent values of c (\alpha) which are considered. For example if the first two values of c are c=3 and c=7, the first column name of this table is c3_v_c7 to denote that the entry of this column are the ARI indexes between c=3 and c=7 Remark: field ARICLAtable is present only if 'whichIC' is 'ALL' or 'whichIC' is 'CLACLA' |
MIXCLAbsIDX |
matrix of dimension n-by-NumberOfBestSolutions containing the allocations for MIXCLA associated with the best NumberOfBestSolutions. This field is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXCLA'. |
MIXMIXbsIDX |
matrix of dimension n-by-NumberOfBestSolutions containing the allocations for MIXXMIX associated with the best NumberOfBestSolutions. This field is present only if 'whichIC' is 'ALL' or 'whichIC' is 'MIXMIX'. |
CLACLAbsIDX |
matrix of dimension n-by-NumberOfBestSolutions containing the allocations for CLACLA associated with the best NumberOfBestSolutions. This field is present only if 'whichIC' is 'ALL' or 'whichIC' is 'CLACLA'. |
kk |
vector containing the values of k (number of components) which have been considered. This vector is equal to input optional argument kk if kk had been specified else it is equal to 1:5. |
cc |
vector containing the values of c (values of the restriction factor) which have been considered. This vector is equal to input argument Ic.cc. |
alpha |
vector containing the values of \alpha (values of the trimming level) which have been considered. This vector is equal to input argument IC.alpha. |
References
Cerioli, A., Garcia-Escudero, L.A., Mayo-Iscar, A. and Riani M. (2017), Finding the Number of Groups in Model-Based Clustering via Constrained Likelihoods, "Journal of Computational and Graphical Statistics", pp. 404-416, https://doi.org/10.1080/10618600.2017.1390469
Hubert L. and Arabie P. (1985), Comparing Partitions, "Journal of Classification", Vol. 2, pp. 193-218.
See Also
tclustIC
|
tclust
|
tclustregIC
|
tclustreg
|
carbikeplot