FSRinvmdr
FSRinvmdr converts values of mdr into confidence levels and mdr in normal coordinates
Description
Examples
FSRinvmdr with all default options.
Example of finding the confidence level of MDRenv, where MDRenv is the matrix of 99 per cent confidence envelopes based on 1000 observations and 5 explanatory variables.
% MDRinv is a matrix which in the second column contains
% all values equal to 0.99
p=5;
MDRenv=FSRenvmdr(1000,p,'prob',0.99);
MDRinv=FSRinvmdr(MDRenv,p);
 FSRinvmdr with optional arguments.
FSRinvmdr with optional arguments.
 FSRinvmdr with optional arguments.
FSRinvmdr with optional arguments.Example of finding confidence level of mdr for untransformed wool data.
% In the example, the values of mdr are plotted and then transformed
% into observed confidence levels.
% The output is plotted in normal coordinates.
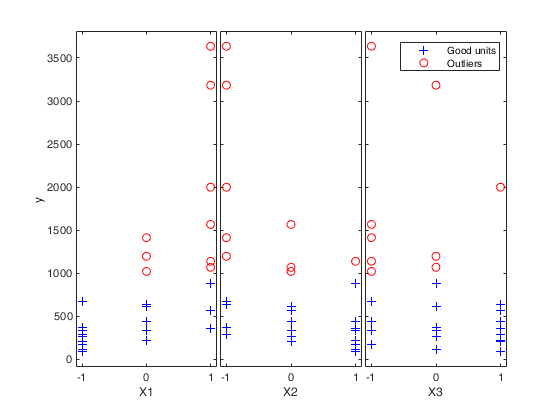
load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
% The line below shows the plot of mdr
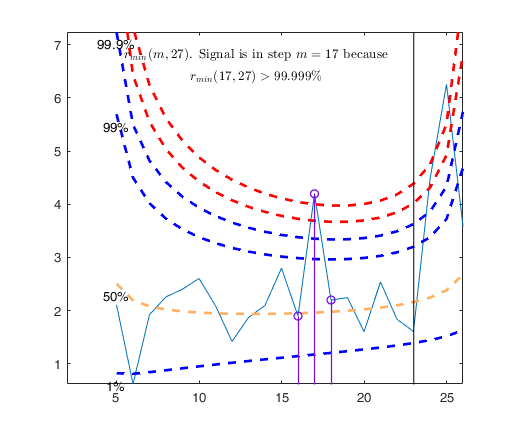
[out]=FSR(y,X,'nsamp',0,'plots',1);
MDRinv=FSRinvmdr(out.mdr,size(X,2)+1,'plots',1);
------------------------------
Warning: Number of subsets without full rank equal to 16.6%
-------------------------
Signal detection loop
Tentative signal in central part of the search: step m=17 because
rmin(17,27)>99.999%
-------------------
Signal validation exceedance of upper envelopes
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=16
Superimposition stopped because r_{min}(17,19)>99% envelope
$r_{min}(17,19)>99$\% envelope
Subsample of 18 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=9
Summary of the exceedances
1 99 999 9999 99999
1 3 3 3 2
Related Examples
Resuperimposing envelopes.
Comparison of resuperimposing envelopes using mdr coordinates and normal coordinates again on wool data.
load('wool.txt','wool');
y=wool(:,4);
X=wool(:,1:3);
% The line below shows the plot of mdr
[out]=FSR(y,X,'nsamp',0,'plots',2);
n0=16:19;
quantplo=[0.01 0.5 0.99 0.999 0.9999 0.99999];
ninv=norminv(quantplo);
lwdenv=2;
ij=0;
supn0=max(n0);
for jn0=n0;
ij=ij+1;
MDRinv = FSRinvmdr(out.mdr,4,'n',jn0);
% Resuperimposed envelope in normal coordinates
subplot(2,2,ij)
plot(MDRinv(:,1),norminv(MDRinv(:,2)),'LineWidth',2)
xlim([0 supn0])
v=axis;
line(v(1:2)',[ninv;ninv],'color','g','LineWidth',lwdenv,'LineStyle','--','Tag','env');
text(v(1)*ones(length(quantplo),1),ninv',strcat(num2str(100*quantplo'),'%'));
% line(MDRinv(:,1),norminv(MDRinv(:,2)),'LineWidth',2)
title(['Resuperimposed envelope n=' num2str(jn0)]);
end
Example with Hospital Data.
Comparison of resuperimposing envelopes using mdr coordinates and normal coordinates at particular steps.
load('hospitalFS.txt');
y=hospitalFS(:,5);
X=hospitalFS(:,1:4);
% exploratory analysis through the yXplot
out=FSR(y,X,'nsamp',20000,'plots',2,'lms',0);
n0=[54 58 62 63];
quantplo=[0.01 0.5 0.99 0.999 0.9999 0.99999];
ninv=norminv(quantplo);
lwdenv=2;
supn0=max(n0);
figure;
ij=0;
for jn0=n0;
ij=ij+1;
[MDRinv] = FSRinvmdr(out.mdr,5,'n',jn0);
% Plot for each step of the fwd search the values of mdr translated in
% terms of normal quantiles
subplot(2,2,ij)
plot(MDRinv(:,1),norminv(MDRinv(:,2)),'LineWidth',2)
xlim([0 supn0])
v=axis;
line(v(1:2)',[ninv;ninv],'color','g','LineWidth',lwdenv,'LineStyle','--','Tag','env');
text(v(1)*ones(length(quantplo),1),ninv',strcat(num2str(100*quantplo'),'%'));
line(MDRinv(:,1),norminv(MDRinv(:,2)),'LineWidth',2)
title(['Resuperimposed envelope n=' num2str(jn0)]);
end
Example with input passed as struct.
load('hospitalFS.txt');
y=hospitalFS(:,5);
X=hospitalFS(:,1:4);
n=length(y);
% Prepare input for Figure 4.30
% LMS using all subsamples (very lengthy)
computeLMSusingAllSubsets=false;
if computeLMSusingAllSubsets ==true
nsamp=0;
[outLXS]=LXS(y,X,'nsamp',nsamp);
else
% best out of 111,469,176 subsets
outLXS=struct;
outLXS.bs= [ 3 11 20 23 74];
end
p=size(X,2)+1;
outFS=FSReda(y,X,outLXS.bs);
% Transform minimum deletion residual from standard coordinates to normal
% coordinates
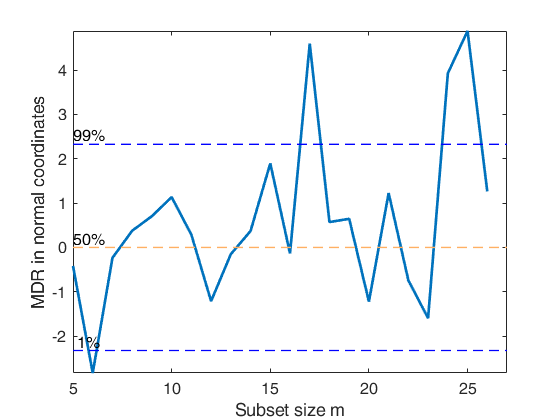
outFS1=FSRinvmdr(outFS,p);
% Minimum deletion residuals in normal coordinates (Figure 4.30 of the
% forthcoming book ARCPT 2024)
mdrplot(outFS1,'ncoord',true,'quant',[0.1 0.5 0.99 0.999 0.9999]);
Input Arguments
mdrInput — Object containing values of minimum deletion residuals.
Matrix or struct.
If mdrInput is a matrix, it has 2 or 3 columns and contains: 1st col = fwd search index;
2nd col = minimum deletion residual (possibly stored with sign).
If mdrInput is a struct, it must contain mdrInput.mdr = matrix which contains in the second column the values of the minimum deletion residual.
Data Types: array or struct
p — Number of explanatory variables.
Scalar.
Number of explanatory variables of the underlying dataset (including the intercept if present)
Data Types: numeric scalar
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'n',10
, 'plots',1
n
—size of the sample.scalar.
If it is not specified it is set equal to mdr(end,1)+1
Example: 'n',10
Data Types: double
plots
—Plot on the screen.scalar | structure.
It specify whether it is necessary to plot in normal coordinates the value of mdr.
If plots = 1, a plot which shows the confidence level of mdr in each step is shown on the screen.
Remark. Three horizontal lines associated respectively with values 0.01 0.5 and 0.99 are added to the plot.
If plots is a structure, the user can specify the following options: conflev = vector containing horizontal lines associated with confidence levels conflevlab = scalar if it is equal 1 labels associated with horizontal lines are shown on the screen xlim = minimum and maximum on the x axis ylim = minimum and maximum on the y axis LineWidth = Line width of the trajectory of mdr in normal coordinates LineStyle = Line style of the trajectory of mle of transformation parameters LineWidthEnv = Line width of the horizontal lines Tag = tag of the plot (default is pl_mdrinv) FontSize = font size of the text labels which identify the trajectories
Example: 'plots',1
Data Types: double
Output Arguments
mdrOutput — description
Structure
Object containing values of mdr in normal coordinates.
Matrix or structure depending on the input mdrInput.
If input mdrInput is a matrix, mdrOutput is a matrix with the same rows of input and 3 columns: 1st col = fwd search index.
2nd col = confidence level of each value of mdr.
3rd col = mdr in normal coordinates (50 conf level becomes norminv(0.50)=0; 99 conf level becomes norminv(0.99)=2.33).
If input mdrInput is a struct, mdrOutput is a struct with all the fields of the input structure mdrInput except that now the field mdr is referred to normal coordinates.
| Value | Description |
|---|---|
mdr |
value of mdr in normal coordinates. |
References
Atkinson, A.C. and Riani, M. (2006), Distribution theory and simulations for tests of outliers in regression, "Journal of Computational and Graphical Statistics", Vol. 15, pp. 460-476.
Riani, M. and Atkinson, A.C. (2007), Fast calibrations of the forward search for testing multiple outliers in regression, "Advances in Data Analysis and Classification", Vol. 1, pp. 123-141.