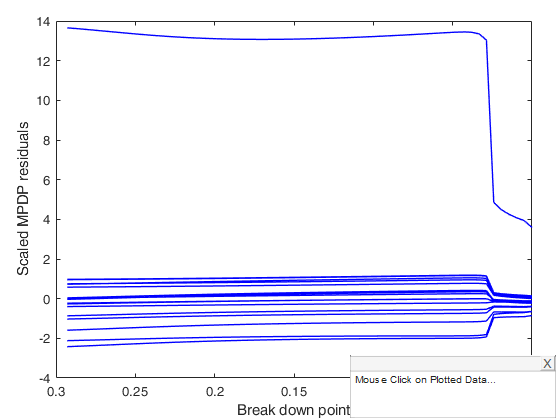
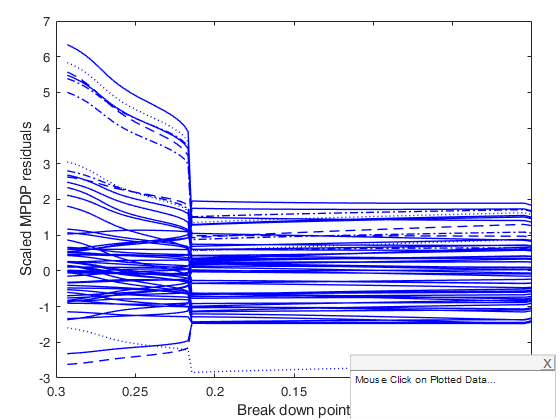
mdpdReda
mdpdReda allows to monitor Minimum Density Power Divergence criterion to parametric regression problems.
Description
Examples
Call of mdpdReda with all default options.
Simulate a regression model.
n=100; p=3; sig=0.01; eps=randn(n,1); X=randn(n,p); bet=3*ones(p,1); y=X*bet+sig*eps; % Contaminate the first 10 observations. y(1:10)=y(1:10)+0.05; [out] = mdpdReda(y, X,'plots',1);
Example of use of option alpha.
n=100; p=3; sig=0.01; eps=randn(n,1); X=randn(n,p); bet=3*ones(p,1); y=X*bet+sig*eps; % Contaminate the first 10 observations. y(1:10)=y(1:10)+0.05; [out] = mdpdReda(y, X,'plots',1,'alphaORbdp','alpha','tuningpar',[1 0.8 0.2 0]);
Related Examples
mdpdReda applied to example 1 of Durio and Isaia (2011).
600 points generated according to the model Y=0.5*X1+0.5*X2+eps and n2 = 120 points (outliers), drawn from the model X1,X2~U(0,1) eps~N(0,0.1^2)
n=600; p=2; sig=0.1; eps=randn(n,1); X=rand(n,p); bet=0.5*ones(p,1); y=X*bet+sig*eps; [out] = mdpdReda(y,X ,'plots',1);
mdpdReda applied to Forbes data.
mdpdReda applied to Forbes data.
load('forbes.txt');
y=forbes(:,2);
X=forbes(:,1);
[outalpha0] = mdpdReda(y, X, 'plots',1);
mdpdReda applied to multiple regression data.
mdpdReda applied to multiple regression data.
load('multiple_regression.txt');
y=multiple_regression(:,4);
X=multiple_regression(:,1:3);
[out] = mdpdReda(y, X, 'plots',1);
Input Arguments
y — Response variable.
Vector.
Response variable, specified as a vector of length n, where n is the number of observations. Each entry in y is the response for the corresponding row of X.
Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: double
X — Predictor variables.
Matrix.
Matrix of explanatory variables (also called 'regressors') of dimension n x (p-1) where p denotes the number of explanatory variables including the intercept.
Rows of X represent observations, and columns represent variables. By default, there is a constant term in the model, unless you explicitly remove it using input option intercept, so do not include a column of 1s in X. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.
Data Types: double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'tuningpar',[1 0.8 0.5 0.4 0.3 0.2 0.1]
, 'alphaORbdp','bdp'
, 'modelfun', modelfun where modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
, 'beta0',[0.5 0.2 0.1]
, 'intercept',true
, 'conflev',0.99
, 'plots',0
tuningpar
—tuning parameter.scalar | Vector.
tuningpar may refer to $\alpha$ (default) or to breakdown point (depending on input option alphaORbdp.
As the tuning parameter $\alpha$ (bdp) decreases the robustness of the Minimum Density Power Divergence estimator decreases while its efficiency increases (Basu et al., 1998). For $\alpha=0$ the MDPDE becomes the Maximum Likelihood estimator, while for $\alpha=1$ the divergence yields the $L_2$ metric and the estimator minimizes the $L_2$ distance between the densities, e.g., Scott (2001), Durio and Isaia (2003). The sequence is forced to be monotonically decreasing, e.g. alpha=[1 0.9 0.5 0.01]. The default for tuningpar is a sequence from 1 to 0 with step -0.01.
Example: 'tuningpar',[1 0.8 0.5 0.4 0.3 0.2 0.1]
Data Types: double
alphaORbdp
—ctuning refers to $\alpha$ or to breakdown point.character.
Character which specifies what are the values in input option tuningpar. If this option is not specified or it is equal to 'alpha' then program assumes that the values of tuningpar refer to 'alpha', elseif this option is equal to 'bdp', program assumes that the values of tuninpar refer to breakdownpoint.
Example: 'alphaORbdp','bdp'
Data Types: char
modelfun
—non linear function to use.function_handle | empty value (default).
If modelfun is empty the link between $X$ and $\beta$ is assumed to be linear else it is necessary to specify a function (using @) that accepts two arguments, a coefficient vector and the array X and returns the vector of fitted values from the non linear model y. For example, to specify the hougen (Hougen-Watson) nonlinear regression function, use the function handle @hougen.
Example: 'modelfun', modelfun where modelfun = @(beta,X) X*beta(1).*exp(-beta(2)*X);
Data Types: function_handle or empty value
theta0
—empty value or vector containing initial values for the
coefficients (beta0 and sigma0) just in case modelfun is
non empty.if modelfun is empty this argument is ignored and LMS solution will be used as initial solution for the minimization.
Example: 'beta0',[0.5 0.2 0.1]
Data Types: double
intercept
—Indicator for constant term.true (default) | false.
If true, and modelfun is empty (that is if the link between X and beta is linear) a model with constant term will be fitted (default), else no constant term will be included.
This argument is ignored if modelfun is not empty.
Example: 'intercept',true
Data Types: boolean
conflev
—Confidence level.scalar.
Confidence level which is used to declare units as outliers.
Usually conflev=0.95, 0.975 0.99 (individual alpha) or 1-0.05/n, 1-0.025/n, 1-0.01/n (simultaneous alpha).
Default value is 0.975.
Example: 'conflev',0.99
Data Types: double
plots
—Plot on the screen.scalar.
If plots = 1, generates a plot of the monitoring of residuals against alpha.
Example: 'plots',0
Data Types: single | double
Output Arguments
out — description
Structure
A structure containing the following fields
| Value | Description |
|---|---|
Beta |
matrix containing the mpdp estimator of regression coefficients for each value of alpha |
Scale |
vector containing the estimate of the scale (sigma) for each value of alpha. |
RES |
n x length(alpha) matrix containing the robust scaled residuals for each value of bdp |
Outliers |
Boolean matrix containing the list of the units declared as outliers for each value of alpha using confidence level specified in input scalar conflev |
conflev |
confidence level which is used to declare outliers. |
alpha |
vector which contains the values of alpha which have been used. To each value of alpha corresponds a value of bdp (see out.bdp). |
bdp |
vector which contains the values of bdp which have been used. To each value of bdp corresponds a value of alpha (see out.alpha). |
y |
response vector y. The field is present if option yxsave is set to 1. |
X |
data matrix X. The field is present if option yxsave is set to 1. |
class |
'MDPDReda' |
Fval |
Value of the objective function and reason fminunc or fminsearch stopped and v. Matrix. length(alpha)-by-3 matrix. The first column contains the values of alpha which have been considered. The second column contains the values of the objective function at the solution. The third column contins the details about convergence. A value greater then 0 denotes normal convergence. See help of functions fminunc or fminsearch for further details. |
More About
Additional Details
We assume that the random variables $Y|x$ are distributed as normal $N( \eta(x,\beta), \sigma_0)$ random variable with density function $\phi$.
Note that if the model is linear $\eta(x,\beta)= x^T \beta$. The estimate of the vector $\theta_\alpha=(\beta_1, \ldots, \beta_p)^T$ (Minimum Density Power Divergence Estimate) is given by:
\[ \mbox{argmin}_{\beta, \sigma} \left[ \frac{1}{\sigma^\alpha \sqrt{ (2 \pi)^\alpha(1+\alpha)}}-\frac{\alpha+1}{\alpha} \frac{1}{n} \sum_{i=1}^n \phi^\alpha (y_i| \eta (x_i, \beta), \sigma) \right] \] As the tuning paramter $\alpha$ increases, the robustness of the Minimum Density Power Divergence Estimator (MDPDE) increases while its efficieny decreases (Basu et al. 1998). For $\alpha=0$ the MDPDE becomes the Maximum Likelihood Estimator, while for $\alpha=1$ the estimator minimizes the $L_2$ distance between the densities (Durio and Isaia, 2003),References
Basu, A., Harris, I.R., Hjort, N.L. and Jones, M.C., (1998), Robust and efficient estimation by minimizing a density power divergence, "Biometrika", Vol. 85, pp. 549-559.
69-83.
Durio A., Isaia E.D. (2011), The Minimum Density Power Divergence Approach in Building Robust Regression Models, "Informatica", Vol. 22, pp. 43-56.