moonplot
moonplot draws the Correspondence Analysis (CA) moonplot.
Examples
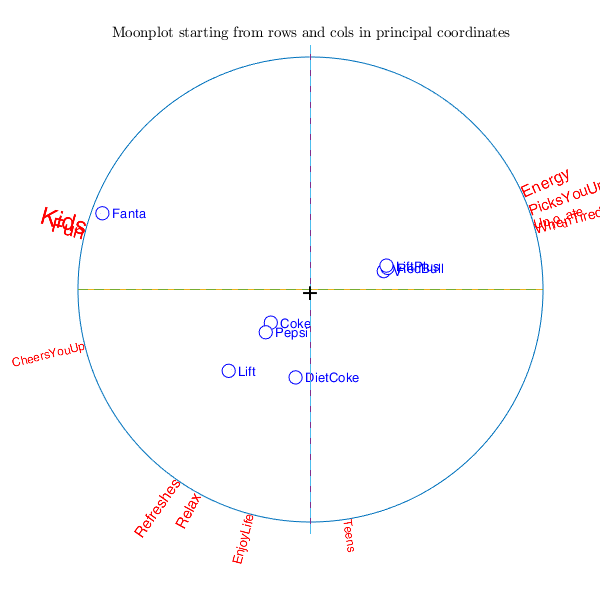
 moonplot with all the default options.
moonplot with all the default options.
 moonplot with all the default options.
moonplot with all the default options.Prepare the data.
load('csdPerceptions')
N=csdPerceptions;
out=CorAna(N,'plots',0);
moonplot(out);Summary
Singular_value Inertia Accounted_for Cumulative
______________ _______ _____________ __________
dim_1 0.54 0.29 0.78 0.78
dim_2 0.25 0.06 0.17 0.95
dim_3 0.11 0.01 0.03 0.98
dim_4 0.09 0.01 0.02 1.00
dim_5 0.02 0.00 0.00 1.00
dim_6 0.01 0.00 0.00 1.00
dim_7 0.01 0.00 0.00 1.00
ROW POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Coke -0.24 0.05 0.52
V 0.45 0.14 0.93
RedBull 0.47 0.14 0.92
LiftPlus 0.46 0.08 0.90
DietCoke -0.09 0.00 0.02
Fanta -1.27 0.54 0.88
Lift -0.50 0.03 0.34
Pepsi -0.27 0.01 0.36
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Coke -0.20 0.17 0.36
V 0.11 0.04 0.06
RedBull 0.13 0.05 0.07
LiftPlus 0.15 0.04 0.09
DietCoke -0.54 0.16 0.76
Fanta 0.47 0.33 0.12
Lift -0.50 0.15 0.34
Pepsi -0.26 0.06 0.33
COLUMN POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Kids -1.32 0.43 0.92
Teens 0.04 0.00 0.02
EnjoyLife -0.08 0.00 0.06
PicksYouUp 0.49 0.10 0.88
Refreshes -0.29 0.02 0.21
CheersYouUp -0.24 0.01 0.83
Energy 0.60 0.14 0.81
Up_to_date 0.29 0.03 0.88
Fun -0.92 0.20 0.92
WhenTired 0.45 0.07 0.93
Relax -0.25 0.01 0.20
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Kids 0.37 0.15 0.07
Teens -0.24 0.16 0.65
EnjoyLife -0.29 0.13 0.79
PicksYouUp 0.18 0.06 0.11
Refreshes -0.42 0.16 0.44
CheersYouUp -0.06 0.00 0.05
Energy 0.27 0.14 0.17
Up_to_date 0.08 0.01 0.07
Fun 0.23 0.06 0.06
WhenTired 0.12 0.02 0.07
Relax -0.45 0.11 0.67
-----------------------------------------------------------
Overview ROW POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
____ _______ _______ _______ _____________ _____________ _____________ _____________
Coke 0.27 -0.24 -0.20 0.03 0.05 0.17 0.52 0.36
V 0.21 0.45 0.11 0.05 0.14 0.04 0.93 0.06
RedBull 0.18 0.47 0.13 0.04 0.14 0.05 0.92 0.07
LiftPlus 0.11 0.46 0.15 0.03 0.08 0.04 0.90 0.09
DietCoke 0.04 -0.09 -0.54 0.01 0.00 0.16 0.02 0.76
Fanta 0.10 -1.27 0.47 0.18 0.54 0.33 0.88 0.12
Lift 0.04 -0.50 -0.50 0.03 0.03 0.15 0.34 0.34
Pepsi 0.06 -0.27 -0.26 0.01 0.01 0.06 0.36 0.33
Overview COLUMN POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
____ _______ _______ _______ _____________ _____________ _____________ _____________
Kids 0.07 -1.32 0.37 0.14 0.43 0.15 0.92 0.07
Teens 0.18 0.04 -0.24 0.02 0.00 0.16 0.02 0.65
EnjoyLife 0.10 -0.08 -0.29 0.01 0.00 0.13 0.06 0.79
PicksYouUp 0.12 0.49 0.18 0.03 0.10 0.06 0.88 0.11
Refreshes 0.06 -0.29 -0.42 0.02 0.02 0.16 0.21 0.44
CheersYouUp 0.06 -0.24 -0.06 0.00 0.01 0.00 0.83 0.05
Energy 0.12 0.60 0.27 0.05 0.14 0.14 0.81 0.17
Up_to_date 0.09 0.29 0.08 0.01 0.03 0.01 0.88 0.07
Fun 0.07 -0.92 0.23 0.06 0.20 0.06 0.92 0.06
WhenTired 0.09 0.45 0.12 0.02 0.07 0.02 0.93 0.07
Relax 0.03 -0.25 -0.45 0.01 0.01 0.11 0.20 0.67
-----------------------------------------------------------
Legend
CntrbPnt2In = relative contribution of points to explain total Inertia of the latent dimension
The sum of the numbers in a column is equal to 1
CntrbDim2In = relative contribution of latent dimension to explain total Inertia of a point
CntrbDim2In_1+CntrbDim2In_2+...+CntrbDim2In_K=1
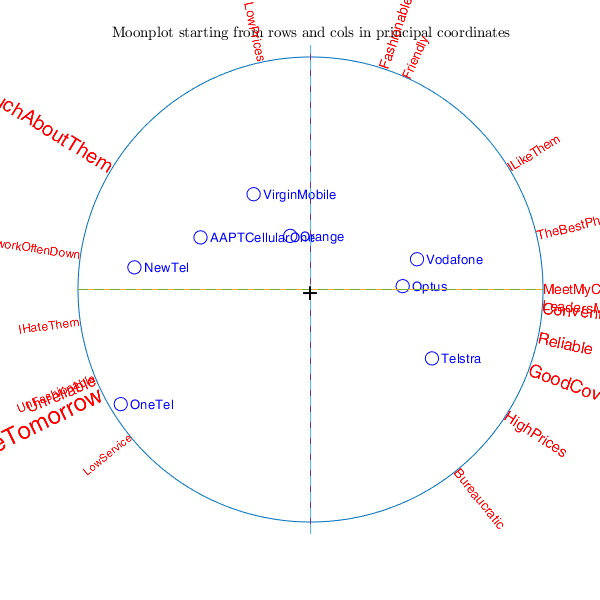
 moonplot with option changedimsign.
moonplot with option changedimsign.
 moonplot with option changedimsign.
moonplot with option changedimsign.Prepare the data.
load mobilephone out=CorAna(mobilephone,'plots',0); % Use of option changedimsign moonplot(out,'changedimsign',[true false])
Summary
Singular_value Inertia Accounted_for Cumulative
______________ _______ _____________ __________
dim_1 0.48 0.23 0.66 0.66
dim_2 0.25 0.06 0.19 0.84
dim_3 0.20 0.04 0.12 0.96
dim_4 0.09 0.01 0.02 0.98
dim_5 0.06 0.00 0.01 1.00
dim_6 0.03 0.00 0.00 1.00
dim_7 0.02 0.00 0.00 1.00
ROW POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
AAPTCellularOne 0.44 0.07 0.58
NewTel 0.70 0.19 0.83
OneTel 0.76 0.29 0.68
Optus -0.37 0.10 0.80
Orange 0.08 0.00 0.07
Telstra -0.48 0.20 0.63
VirginMobile 0.23 0.02 0.24
Vodafone -0.42 0.12 0.76
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
AAPTCellularOne 0.21 0.06 0.13
NewTel 0.09 0.01 0.01
OneTel -0.46 0.38 0.25
Optus 0.01 0.00 0.00
Orange 0.21 0.07 0.49
Telstra -0.27 0.22 0.20
VirginMobile 0.38 0.22 0.66
Vodafone 0.12 0.03 0.06
COLUMN POINTS
Results for dimension: 1
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Bureaucratic -0.21 0.01 0.22
LowService 0.13 0.00 0.48
Friendly -0.13 0.00 0.13
LowPrices 0.07 0.00 0.02
Fashionable -0.13 0.00 0.06
UnFashionable 0.26 0.02 0.55
Reliable -0.54 0.06 0.92
HereTodayGoneTomorrow 1.18 0.26 0.76
GoodCoverage -0.73 0.10 0.82
NetworkOftenDown 0.23 0.02 0.78
TheBestPhones -0.33 0.02 0.82
ConvenientlyLocatedStores -0.63 0.09 0.92
HighPrices -0.41 0.03 0.43
Unreliable 0.59 0.08 0.81
MeetMyCommunicationNeeds -0.38 0.03 0.89
LeadersMobilePhoneTechnology -0.43 0.04 0.97
ILikeThem -0.24 0.01 0.57
IHateThem 0.28 0.03 0.95
DonotKnowMuchAboutThem 0.82 0.18 0.58
Results for dimension: 2
Scores CntrbPnt2In CntrbDim2In
______ ___________ ___________
Bureaucratic -0.26 0.06 0.33
LowService -0.11 0.01 0.31
Friendly 0.29 0.07 0.63
LowPrices 0.33 0.09 0.52
Fashionable 0.39 0.12 0.56
UnFashionable -0.10 0.01 0.09
Reliable -0.12 0.01 0.04
HereTodayGoneTomorrow -0.58 0.22 0.18
GoodCoverage -0.27 0.05 0.11
NetworkOftenDown 0.03 0.00 0.02
TheBestPhones 0.08 0.00 0.05
ConvenientlyLocatedStores -0.05 0.00 0.01
HighPrices -0.26 0.04 0.18
Unreliable -0.25 0.05 0.14
MeetMyCommunicationNeeds 0.00 0.00 0.00
LeadersMobilePhoneTechnology -0.03 0.00 0.00
ILikeThem 0.15 0.02 0.22
IHateThem -0.04 0.00 0.02
DonotKnowMuchAboutThem 0.50 0.25 0.22
-----------------------------------------------------------
Overview ROW POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
____ _______ _______ _______ _____________ _____________ _____________ _____________
AAPTCellularOne 0.09 0.44 0.21 0.03 0.07 0.06 0.58 0.13
NewTel 0.09 0.70 0.09 0.05 0.19 0.01 0.83 0.01
OneTel 0.12 0.76 -0.46 0.10 0.29 0.38 0.68 0.25
Optus 0.17 -0.37 0.01 0.03 0.10 0.00 0.80 0.00
Orange 0.10 0.08 0.21 0.01 0.00 0.07 0.07 0.49
Telstra 0.19 -0.48 -0.27 0.07 0.20 0.22 0.63 0.20
VirginMobile 0.10 0.23 0.38 0.02 0.02 0.22 0.24 0.66
Vodafone 0.15 -0.42 0.12 0.04 0.12 0.03 0.76 0.06
Overview COLUMN POINTS
Mass Score_1 Score_2 Inertia CntrbPnt2In_1 CntrbPnt2In_2 CntrbDim2In_1 CntrbDim2In_2
____ _______ _______ _______ _____________ _____________ _____________ _____________
Bureaucratic 0.05 -0.21 -0.26 0.01 0.01 0.06 0.22 0.33
LowService 0.06 0.13 -0.11 0.00 0.00 0.01 0.48 0.31
Friendly 0.05 -0.13 0.29 0.01 0.00 0.07 0.13 0.63
LowPrices 0.05 0.07 0.33 0.01 0.00 0.09 0.02 0.52
Fashionable 0.05 -0.13 0.39 0.01 0.00 0.12 0.06 0.56
UnFashionable 0.06 0.26 -0.10 0.01 0.02 0.01 0.55 0.09
Reliable 0.05 -0.54 -0.12 0.02 0.06 0.01 0.92 0.04
HereTodayGoneTomorrow 0.04 1.18 -0.58 0.08 0.26 0.22 0.76 0.18
GoodCoverage 0.04 -0.73 -0.27 0.03 0.10 0.05 0.82 0.11
NetworkOftenDown 0.07 0.23 0.03 0.00 0.02 0.00 0.78 0.02
TheBestPhones 0.05 -0.33 0.08 0.01 0.02 0.00 0.82 0.05
ConvenientlyLocatedStores 0.05 -0.63 -0.05 0.02 0.09 0.00 0.92 0.01
HighPrices 0.04 -0.41 -0.26 0.02 0.03 0.04 0.43 0.18
Unreliable 0.05 0.59 -0.25 0.02 0.08 0.05 0.81 0.14
MeetMyCommunicationNeeds 0.05 -0.38 0.00 0.01 0.03 0.00 0.89 0.00
LeadersMobilePhoneTechnology 0.05 -0.43 -0.03 0.01 0.04 0.00 0.97 0.00
ILikeThem 0.05 -0.24 0.15 0.01 0.01 0.02 0.57 0.22
IHateThem 0.08 0.28 -0.04 0.01 0.03 0.00 0.95 0.02
DonotKnowMuchAboutThem 0.06 0.82 0.50 0.07 0.18 0.25 0.58 0.22
-----------------------------------------------------------
Legend
CntrbPnt2In = relative contribution of points to explain total Inertia of the latent dimension
The sum of the numbers in a column is equal to 1
CntrbDim2In = relative contribution of latent dimension to explain total Inertia of a point
CntrbDim2In_1+CntrbDim2In_2+...+CntrbDim2In_K=1
Input Arguments
out — Structure containing the output of function CorAna.
Structure.
Structure containing the following fields.
| Value | Description |
|---|---|
Lr |
cell of length $I$ containing the labels of active rows (i.e. the rows which participated to the fit). |
Lc |
cell of length $J$ containing the labels of active columns (i.e. the columns which participated to the fit). |
n |
Grand total. out.n is equal to sum(sum(out.N)). This is the number of observations. |
Dr |
Square matrix of size $I$ containing on the diagonal the row masses. This is matrix $D_r$. \[ D_r=diag(r) \] |
Dc |
Square matrix of size $J$ containing on the diagonal the column masses. This is matrix $D_c$. \[ D_c=diag(c) \] |
InertiaExplained |
matrix with 4 columnn. - First column contains the singular values (the sum of the squared singular values is the total inertia). - Second column contains the eigenvalues (the sum of the eigenvalues is the total inertia). - Third column contains the variance explained by each latent dimension. - Fourth column contains the cumulative variance explained by each dimension. |
LrSup |
cell containing the labels of the supplementary rows (i.e. the rows whicg did not participate to the fit). |
LcSup |
cell containing the labels of supplementary columns (i.e. the columns which did not participate to the fit). |
SupRowsN |
matrix of size length(LrSup)-by-c referred to supplementary rows. If there are no supplementary rows this field is not present. |
SupColsN |
matlab of size r-by-length(LcSup) referred to supplementary columns. If there are no supplementary columns this field is not present. |
RowsPriSup |
Principal coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
RowsStaSup |
Standard coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
RowsSymSup |
Symmetrical coordinates of supplementary rows. If there are no supplementary rows this field is not present. |
ColsPriSup |
Principal coordinates of supplementary columns. If there are no supplementary columns this field is not present. |
ColsStaSup |
Standard coordinates of of supplementary columns. If there are no supplementary columns this field is not present. |
ColsSymSup |
Symmetrical coordinates of supplementary columns. If there are no supplementary columns this field is not present. |
Data Types: struct
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'plots',plots=struct; plots.colorcols='k'
, 'addx',0.01
, 'addy',0.01
, 'changedimsign', [true false]
, 'xlimx',[-1 1]
, 'ylimy',[0 1]
, 'd1',2
, 'd2',3
,'h',h1 where h1=subplot(2,1,1)
plots
—Customize plot appearance.scalar | structure.
If plots is not a structure, a plot which shows the Principal coordinates of rows and columns is shown on the screen. If plots is a structure it may contain the following fields:
| Value | Description |
|---|---|
alpha |
type of plot, scalar in the interval [0 1] or a string identifying the type of coordinates to use in the plot. If $plots.alpha='rowprincipal'$ the row points are in principal coordinates and the column coordinates are standard coordinates. Distances between row points are (approximated) chi-squared distances (row-metric-preserving). The position of the row points are at the weighted average of the column points. Note that 'rowprincipal' can also be specified setting plots.alpha=1. If $plots.alpha='colprincipal'$, the column coordinates are referred to as principal coordinates and the row coordinates as standard coordinates. Distances between column points are (approximated) chi-squared distances (column-metric-preserving). The position of the column points are at the weighted average of the row points. Note that 'colprincipal' can also be specified setting plots.alpha=0. If $plots.alpha='symbiplot'$, the row and column coordinates are scaled similarly. The sum of weighted squared coordinates for each dimension is equal to the corresponding singular values. These coordinates are often called symmetrical coordinates. This representation is particularly useful if one is primarily interested in the relationships between categories of row and column variables rather than in the distances among rows or among columns. 'symbiplot' can also be specified setting plots.alpha=0.5; If $plots.alpha='bothprincipal'$, both the rows and columns are depicted in principal coordinates. Such a plot is often referred to as a symmetrical plot or French symemtrical model. Note that such a symmetrical plot does not provide a feasible solution in the sense that it does not approximate matrix $D_r^{-0.5}(P-rc')D_c^{-0.5}$. If $plots.alpha='bothstandard'$, both the rows and columns are depicted in standard coordinates. If $plots.alpha='rowgab'$, rows are in principal coordinates and columns are in standard coordinates multiplied by the mass. This biplot has been suggested by Gabriel and Odoroff (1990). If $plots.alpha='colgab'$, columns are in principal coordinates and rows are in standard coordinates multiplied by the mass. This biplot has been suggested by Gabriel and Odoroff (1990). If $plots.alpha='rowgreen'$, rows are in principal coordinates and columns are in standard coordinates multiplied by square root of the mass. This biplot has been suggested by Greenacre and incorporates the contribution of points. In this display, points that contribute very little to the solution, are close to the center of the biplot and are relatively unimportant to the interpretation. This biplot is often referred as contribution biplot because it visually shows the most contributing points (Greenacre 2006b). If $plots.alpha='colgreen'$, columns in principal coordinates and rows in standard coordinates multiplied by the square root of the mass. This biplot has been suggested by Greenacre and incorporates the contribution of points. In this display, points that contribute very little to the solution, are close to the center of the biplot and are relatively unimportant to the interpretation. This biplot is often referred as contribution biplot because it shows visually the most contributing points (Greenacre 2006b). If $plots.alpha=scalar$ in the interval [0 1], row coordinates are given by $D_r^{-1/2} U \Gamma^\alpha$ and column coordinates are given by $D_c^{-1/2} V \Gamma^{1-\alpha}$. Note that for any choice of $\alpha$ the matrix product $ D_r^{-1/2} U \Gamma^\alpha (D_c^{-1/2} V \Gamma^{1-\alpha})^T$ optimally approximates matrix $D_r^{-0.5}(P-rc')D_c^{-0.5}$, in the sense that the sum of squared differences between $D_r^{1/2} D_r^{-1/2} U \Gamma^\alpha (D_c^{-1/2} V \Gamma^{1-\alpha})^T D_c^{1/2}$ and $D_r^{-0.5}(P-rc')D_c^{-0.5}$ is as small as possible. |
FontSize |
scalar which specifies the font size of row labels. The default value is 10. |
FontSizeSup |
scalar which specifies the font size of row labels of supplementary points. The default value is 10. |
MarkerSize |
scalar which specifies the marker size of symbols associated with rows. The default value is 10. |
SymbolRows |
character which specifies the symbol to use for row points. If this field is not present the default symbols is 'o'. |
SymbolRowsSup |
character which specifies the symbol to use for supplementary row points. If this field is not present the default symbols is 'o'. |
ColorRows |
character which specifies the symbol to use for row points or RGB triplet. If this field is not present the default color is 'b'. |
ColorCols |
character which specifies the symbol to use for column points or RGB triplet. If this field is not present the default color is 'r'. |
ColorRowsSup |
character which specifies the symbol to use for row points or RGB triplet. If this field is not present the default color is 'b'. |
ColorColsSup |
character which specifies the symbol to use for supplementary column points or RGB triplet. If this field is not present the default color is 'r'. |
MarkerFaceColorRows |
character which specifies the marker fill color to use for active row points or RGB triplet. If this field is not present the default color is 'auto'. |
MarkerFaceColorRowsSup |
character which specifies the marker fill color to use for supplementary row points or RGB triplet. If this field is not present the default color is 'auto'. |
Example: 'plots',plots=struct; plots.colorcols='k'
Data Types: double
addx
—horizontal displacement for labels.scalar.
Amount of horizontal displacement which has been put on the labels in the plot. The defalut value of addx is 0.04.
Example: 'addx',0.01
Data Types: double
addy
—vertical displacement for labels.scalar.
Amount of vertical displacement which has been put on the labels in the plot. The defalut value of addy is 0.
Example: 'addy',0.01
Data Types: double
changedimsign
—change chosen dimension sign.boolean vector of length 2.
Sometimes for better interpretability it is necessary to change the sign of the coordinates for the chosen dimension. If changedimsign(1) is true the sign of the coordinates for first chosen dimension is changed. If changedimsign(2) is true the sign of the coordinates for first chosen dimension is changed. As default the dimensions are the first and the second however, they can be changed using option plots.dim. The defaul value of changedimsign is [false false] that is the sign is not changed.
Example: 'changedimsign', [true false]
Data Types: boolean
xlimx
—Min and Max of the x axis.vector.
Vector with two elements controlling minimum and maximum of the x axis.
Example: 'xlimx',[-1 1]
Data Types: double
ylimy
—Min and Max of the y axis.vector.
Vector with two elements controlling minimum and maximum of the y axis.
Example: 'ylimy',[0 1]
Data Types: double
d1
—Dimension to show on the horizontal axis.positive integer.
Positive integer in the range 1, 2, .., K which indicates the dimension to show on the x axis. The default value of d1 is 1.
Example: 'd1',2
Data Types: single | double
d2
—Dimension to show on the vertical axis.positive integer.
Positive integer in the range 1, 2, .., K which indicates the dimension to show on the y axis. The default value of d2 is 2.
Example: 'd2',3
Data Types: single | double
h
—the axis handle of a figure where to send the moonplot.this can be used to host the moonplot in a subplot of a complex figure formed by different panels (for example a panel with moonplot from plots.
alpha=0.2 and another with moonplot from plots.alpha=0.5).
Example: 'h',h1 where h1=subplot(2,1,1)
Data Types: Axes object (supplied as a scalar)
Output Arguments
References
Benzecri, J.-P. (1992), "Correspondence Analysis Handbook", New-York, Dekker.
Benzecri, J.-P. (1980), "L'analyse des donnees tome 2: l'analyse des correspondances", Paris, Bordas.
Greenacre, M.J. (1993), "Correspondence Analysis in Practice", London, Academic Press.
Bock, T. (2011), Improving the display of correspondence analysis using moon plots, "International Journal of Market Research", Vol. 53, pp. 307-326.
Gabriel, K.R. and Odoroff, C. (1990), Biplots in biomedical research, "Statistics in Medicine", Vol. 9, pp. 469-485.
Greenacre, M.J. (1993), Biplots in correspondence Analysis, "Journal of Applied Statistics", Vol. 20, pp. 251-269.