simdataset
simdataset simulates and-or contaminates a dataset given the parameters of a finite mixture model with Gaussian components
Syntax
Description
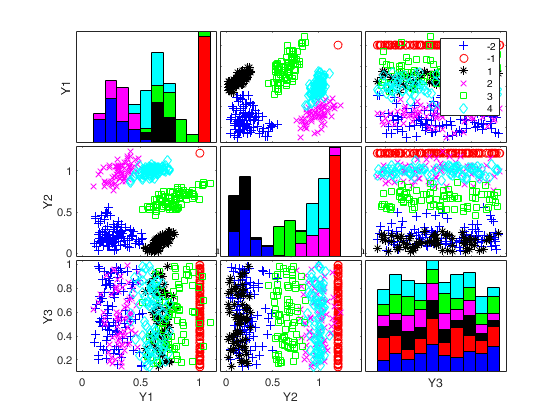
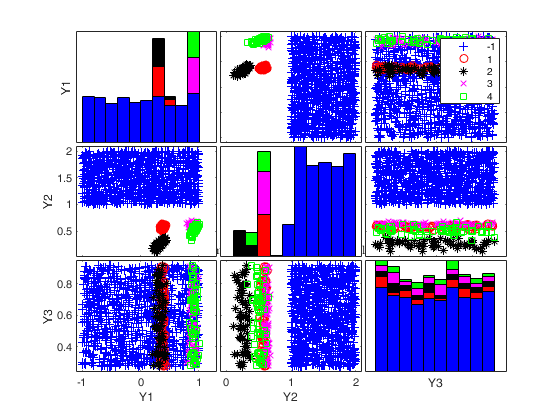
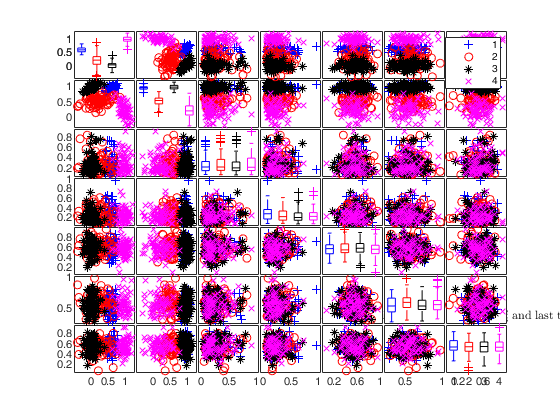
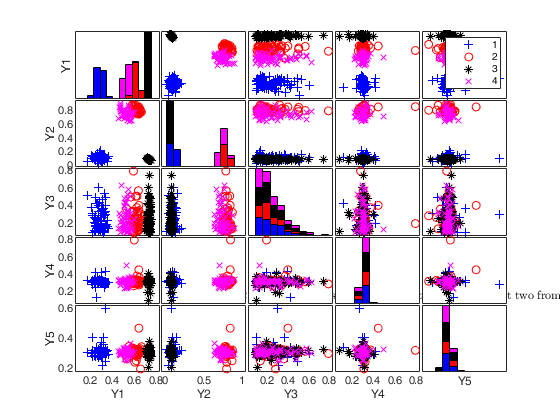
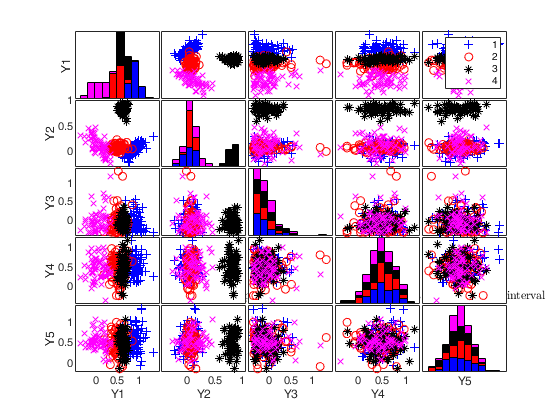
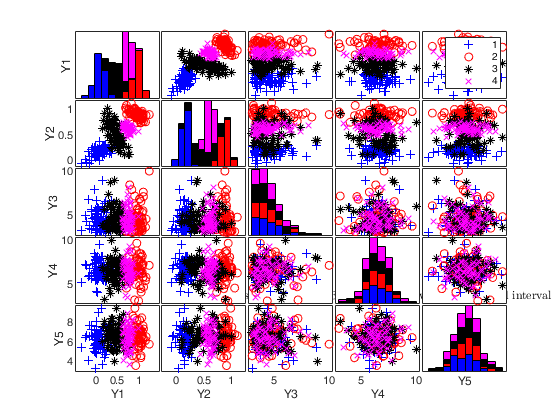
simdataset(n, Pi, Mu, S) generates a matrix of size $n$-by-$p$ containing $n$ observations $p$ dimensions from $k$ groups. More precisely, this function produces a dataset of n observations from a mixture model with parameters 'Pi' (mixing proportions), 'Mu' (mean vectors), and 'S' (covariance matrices). Mixture component sample sizes are produced as a realization from a multinomial distribution with probabilities given by the mixing proportions. For example, if n=200, k=4 and Pi=[0.25, 0.25, 0.25, 0.25] function Nk1=mnrnd( n-k, Pi) is used to generate k integers (whose sum is n-k) from the multinomial distribution with parameters n-k and Pi. The size of the groups is given by Nk1+1. The first Nk1(1)+1 observations are generated using centroid Mu(1,:) and covariance S(:,:,1), ..., the last Nk1(k)+1 observations are generated using centroid Mu(k,:) and covariance S(:,:,k).
DETAILS.
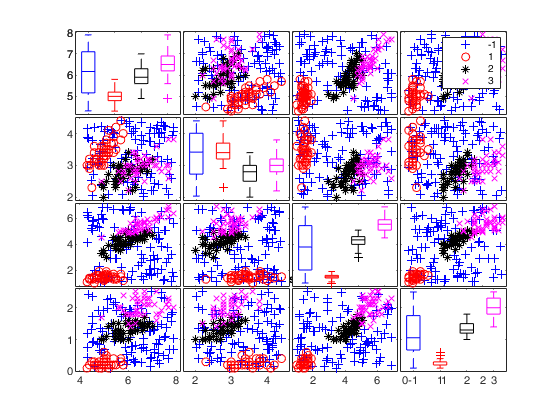
To make a dataset more challenging for clustering, a user might want to simulate noise variables or outliers. The optional parameter 'noiseunits' controls the number and the type of outliers which must be added. The optional parameter 'noisevars' controls the number and the type of noise variables which must be added (it is possible to control the distribution, the interval and the number). Finally, the user can apply an inverse Box-Cox transformation providing a vector of coefficients 'lambda'. The value 1 implies that no transformation is needed for the corresponding coordinate. It is also possible to add outliers to an existing dataset by simply suppling as first argument the matrix of existing data.
Examples
Related Examples
Input Arguments
Output Arguments
References
Maitra, R. and Melnykov, V. (2010), Simulating data to study performance of finite mixture modeling and clustering algorithms, "The Journal of Computational and Graphical Statistics", Vol. 19, pp. 354-376. [to refer to this publication we will use "MM2010 JCGS"]
Melnykov, V., Chen, W.-C. and Maitra, R. (2012), MixSim: An R Package for Simulating Data to Study Performance of Clustering Algorithms, "Journal of Statistical Software", Vol. 51, pp. 1-25.
Davies, R. (1980), The distribution of a linear combination of chi-square random variables, "Applied Statistics", Vol. 29, pp. 323-333.
Riani, M., Cerioli, A., Perrotta, D. and Torti, F. (2015), Simulating mixtures of multivariate data with fixed cluster overlap in FSDA, "Advances in data analysis and classification", Vol. 9, pp. 461-481.
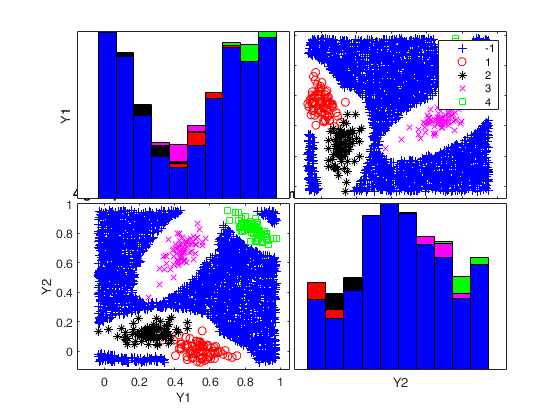
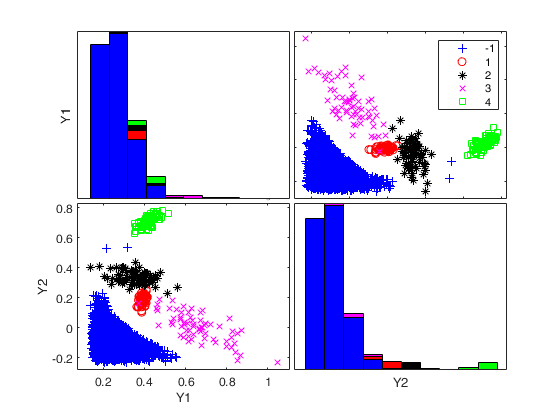
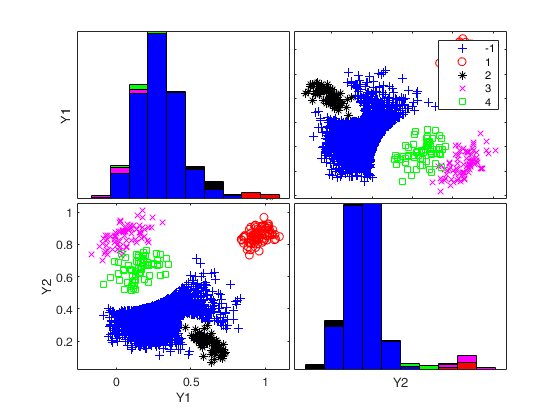
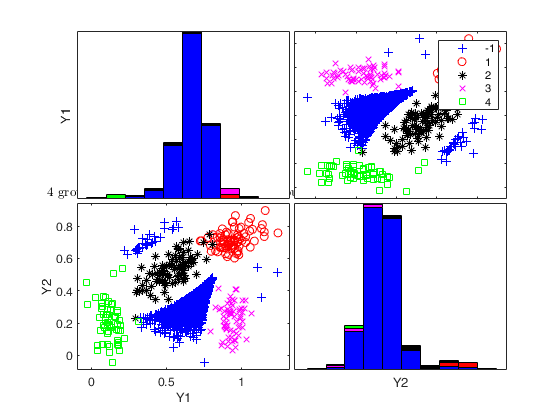
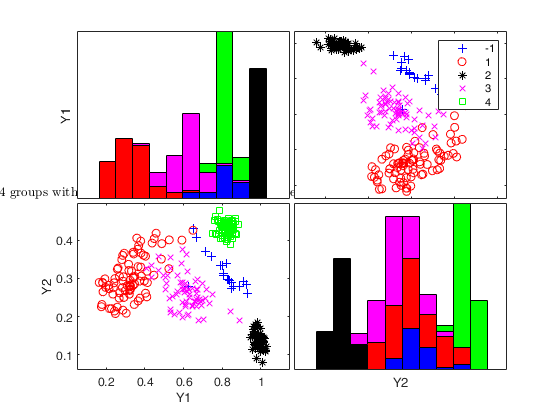
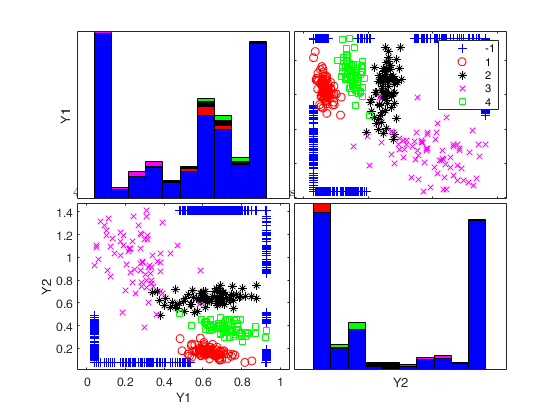
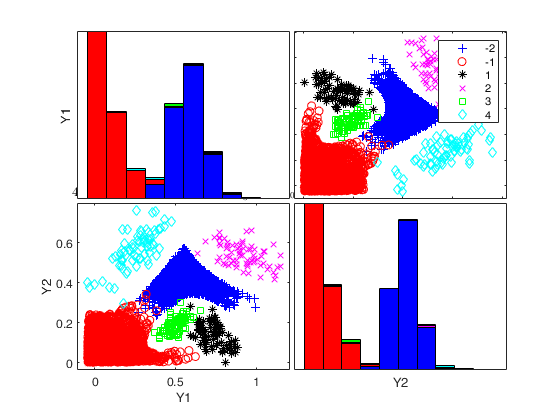
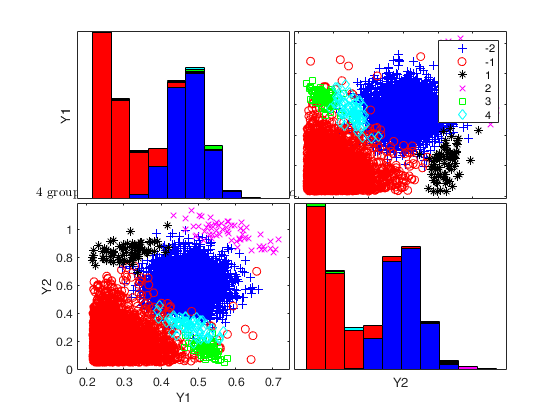
 Generate 4 groups in 2 dimensions and add outliers from uniform distribution.
Generate 4 groups in 2 dimensions and add outliers from uniform distribution.