We assume that the vectors x contains discrete observations from a diffusion
process $x$ following the Ito stochastic differential equation
$$dx(t)= \sigma(t) \ dW(t) + b(t) \ dt,$$
$$d\sigma^2(t)= \gamma(t) \ dZ(t) + a(t) \ dt,$$
where $W$ and $Z$ are two Brownian motions defined on the filtered probability space
$(\Omega, (\mathcal{F}_t)_{t \in [0,T]}, P)$, with correlation $\rho$, while
$\sigma, \gamma, b$ and $a$ are random processes, adapted to $\mathcal{F}_t$.
See the References for further mathematical details.
The spot volatility of volatility at time $t \in [0,T]$ is defined as
$$C(t):=\frac{d\langle \sigma^2,\sigma^2 \rangle_t}{dt}=\gamma^2(t).$$
For any positive integer $n$, let $\mathcal{S}_{n}:=\{ 0=t_{0}\leq \cdots
\leq t_{n}=T \}$ be the observation times. Moreover, let $\delta_l(x):=
x(t_{l+1})-x(t_l)$ be the increments of $x$.
The Fourier estimator of the spot volatility of volatility at time $t \in [0,T]$ is
given by
$$\widehat C_{n,N,M,L}(\tau)= \sum_{|k|\leq L} \left(1-{|k|\over
L}\right)c_k(C_{n,N,M}) \, e^{{\rm i}\frac{2\pi}{T}k\tau},$$
where:
$$c_k(C_{n,N,M})= {T \over {2M+1}} \sum_{|s|\leq M} c_s(d\sigma_{{n},N})c_{k-s}(d\sigma_{{n},N}),$$
$$c_k(d\sigma_{{n},N})={\rm i} \, k\, \frac{2\pi}{T}
c_k(\sigma_{{n},N}), \quad c_k(\sigma_{n,N})={T\over {2N+1}} \sum_{|s|\leq N} c_{s}(dx_{n})c_{k-s}(dx_{n}),$$
$$c_k(dx_{n})= {1\over {T}} \sum_{l=0}^{n-1} e^{-{\rm i}\frac{2\pi}{T}kt_l}\delta_{l}(x).$$
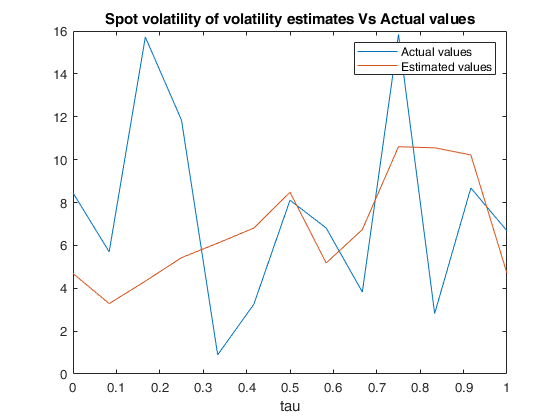
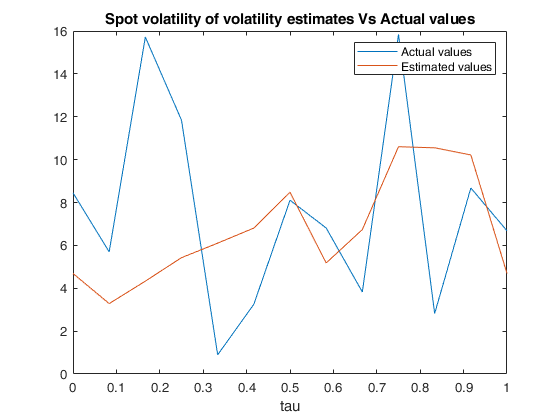
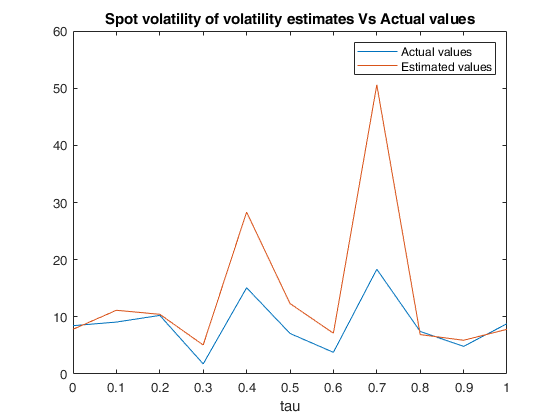
 Example of call of FM_spot_volvol with default values of N,M,L and tau.
Example of call of FM_spot_volvol with default values of N,M,L and tau.