FM_spot_vol
FM_spot_vol computes the spot volatility of a diffusion process via the Fourier-Malliavin estimator
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
References
Mancino, M.E., Recchioni, M.C., Sanfelici, S. (2017), Fourier-Malliavin Volatility Estimation. Theory and Practice, "Springer Briefs in Quantitative Finance", Springer.
Sanfelici, S., Toscano, G. (2024), The Fourier-Malliavin Volatility (FMVol) MATLAB toolbox, available on ArXiv.
See Also
FE_spot_vol
|
FE_spot_vol_FFT
|
FM_spot_quart
|
FM_spot_volvol
|
FM_spot_lev
|
Heston1D
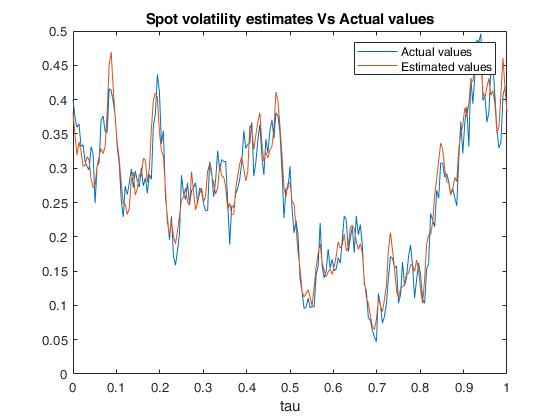
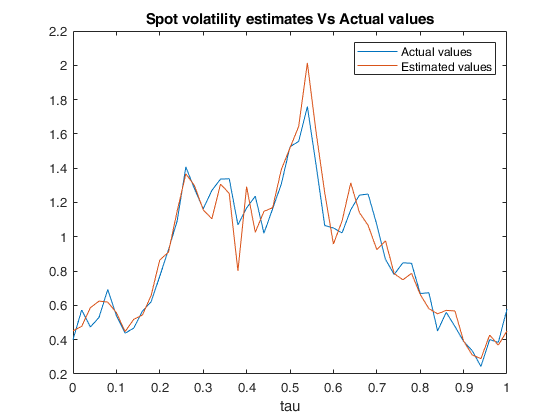
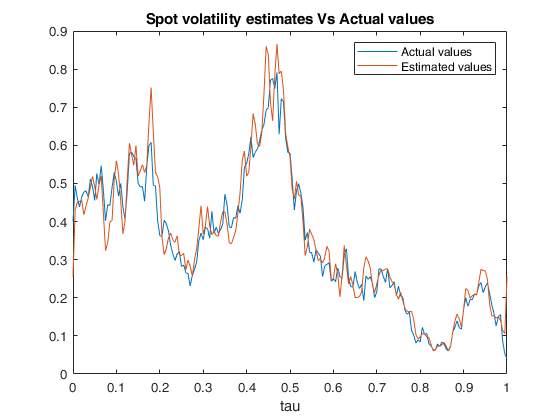
 Example of call of FM_spot_vol with default values of M,N and tau.
Example of call of FM_spot_vol with default values of M,N and tau.