FSRfanTobit

FSRfanTobit monitors the values of the signed sqrt LR test for each lambda in the tobit model

expand all in page

Syntax

Description

example

out =FSRfanTobit(y, X) FSRfanTobit with simulated data.

example

out =FSRfanTobit(y, X, Name, Value) Double censored simulated data.

Examples

expand all

  • FSRfanTobit with simulated data.

    • Generate Tobit regression data 

    rng(200)
n=200;
lambda=0.5;
p=3;
sigma=0.5;
beta=ones(p,1);
X=randn(n,p)+1;
epsilon=randn(n,1);
y=X*beta+sigma*epsilon;
y=normYJ(y,1,lambda,'inverse',true,'Jacobian',true);
qq=quantile(y,0.3);
y(y<=qq)=qq;
left=min(y);
% Compute fanplot for 3 values of lambda
[out]=FSRfanTobit(y,X,'left',left,'la',[0 0.5 1],'init',round(n*0.5));
    Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds 
Warning: interchange greater than 10 when m=100
Total estimated time to complete LMS:  0.01 seconds
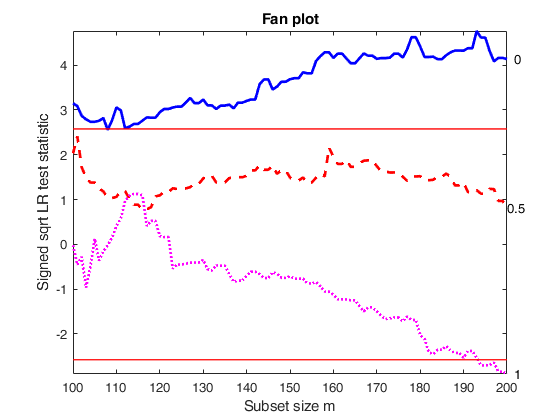
    Click here for the graphical output of this example (link to Ro.S.A. website).

  • Double censored simulated data.

    • rng(4)
n=200;
lambda=0;
p=3;
sigma=0.5;
beta=1*ones(p,1);
X=randn(n,p)+1;
epsilon=randn(n,1);
y=X*beta+sigma*epsilon;
y=normYJ(y,1,lambda,'inverse',true);
% Create left censored observations
qq=quantile(y,0.3);
y(y<=qq)=qq;
% Create right censored observations
qq=quantile(y,0.9);
y(y>=qq)=qq;
% Specify the values of the transformation parameter
la=[-0.5 0 0.5];
left=min(y);
right=max(y);
% Call FSRfanTobit and produce the fanplot
[out]=FSRfanTobit(y,X,'left',left,'right',right,'la',la,'init',round(n*0.5));
    Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds 
Total estimated time to complete LMS:  0.01 seconds 
Warning: interchange greater than 10 when m=100
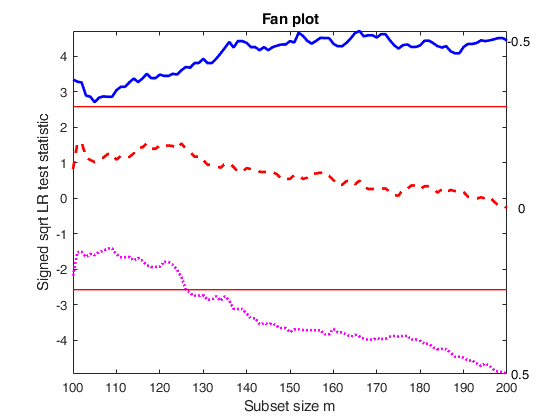
    Click here for the graphical output of this example (link to Ro.S.A. website).

    Related Examples

    Input Arguments

    expand all

    y — Response variable. Vector.

    A vector with n elements that contains the response variable. It can be either a row or a column vector.

    Data Types: single| double

    X — Predictor variables. Matrix.

    Data matrix of explanatory variables (also called 'regressors') of dimension (n x p-1). Rows of X represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations. NOTICE THAT THE INTERCEPT MUST ALWAYS BE INCLUDED.

    Data Types: single| double

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'balancedSearch',false , 'family','YJ' , 'init',100 starts monitoring from step m=100 , 'intercept',false , 'la',[-1 -0.5] , 'left',1 , 'lms',0 , 'msg',false , 'nocheck',true , 'right',800 , 'nsamp',1000 , 'plots',1 , 'conflev',[0.9 0.95 0.99] , 'FontSize',20 , 'labx','my labx' , 'laby','my laby' , 'lwd',5 , 'lwdenv',5 , 'SizeAxesNum',12 , 'titl','my title' , 'xlimx',[0 1] , 'ylimy',[0 1]

    balancedSearch —Balanced search.scalar logical.

    If Balanced search the proportion of observations in the subsets equals (as much as possible) the proportion of units in the sample. The default value of balancedSearch is true.

    Example: 'balancedSearch',false

    Data Types: logical

    family —string which identifies the family of transformations which must be used.character.

    Possible values are 'BoxCox' or 'YJ' (default) The Box-Cox family of power transformations equals $(y^{\lambda}-1)/\lambda$ for $\lambda$ not equal to zero, and $\log(y)$ if $\lambda = 0$.

    The Yeo-Johnson (YJ) transformation is the Box-Cox transformation of $y+1$ for nonnegative values, and of $|y|+1$ with parameter $2-\lambda$ for $y$ negative.

    Remember that BoxCox can be used just if input left is positive. Yeo-Johnson family of transformations does not have this limitation.

    Example: 'family','YJ'

    Data Types: char

    init —Search initialization.scalar.

    It specifies the initial subset size to start monitoring the value of the score test, if init is not specified it will be set equal to: p+1, if the sample size is smaller than 40;

    min(3*p+1,floor(0.5*(n+p+1))), otherwise.

    Example: 'init',100 starts monitoring from step m=100

    Data Types: double

    intercept —Indicator for constant term.true (default) | false.

    Indicator for the constant term (intercept) in the fit, specified as the comma-separated pair consisting of 'Intercept' and either true to include or false to remove the constant term from the model.

    Example: 'intercept',false

    Data Types: boolean

    la —values of the transformation parameter for which it is necessary to compute the LR test.vector.

    Default value of lambda is la=[-1 -0.5 0 0.5 1]; that is the five most common values of lambda

    Example: 'la',[-1 -0.5]

    Data Types: double

    left —left limit for the censored dependent variable.scalar.

    If set to -Inf, the dependent variable is assumed to be not left-censored; default value of left is zero (classical Tobit model).

    Example: 'left',1

    Data Types: double

    lms —Criterion to use to find the initial subset to initialize the search.scalar.

    If lms=1 (default) Least Median of Squares is computed, else Least Trimmed Squares is computed.

    Example: 'lms',0

    Data Types: double

    msg —Level of output to display.boolean.

    Boolean scalar which controls whether to display or not messages on the screen.

    If msg==true (default) messages are displayed on the screen about estimated time to compute the LMS (LTS) for each value of lambda else no message is displayed on the screen

    Example: 'msg',false

    Data Types: logical

    nocheck —Check input arguments.boolean.

    If nocheck is equal to true no check is performed on matrix y and matrix X. Notice that y and X are left unchanged. In other words the additional column of ones for the intercept is not added. As default nocheck=false.

    Example: 'nocheck',true

    Data Types: boolean

    right —right limit for the censored dependent variable.scalar.

    If set to Inf, the dependent variable is assumed to be not right-censored; default value of left is Inf (classical Tobit model).

    Example: 'right',800

    Data Types: double

    nsamp —Number of subsamples which will be extracted to find the initiasl robust estimator.scalar.

    If nsamp=0 all subsets will be extracted. They will be (n choose p). Remark: if the number of all possible subset is <1000, the default is to extract all subsets otherwise just 1000. If nsamp is a matrix of size r-by-p, it contains in the rows the subsets which sill have to be extracted. For example, if p=3 and nsamp=[ 2 4 9; 23 45 49; 90 34 1]; the first subset is made up of units [2 4 9], the second subset of units [23 45 49] and the third subset of units [90 34 1];

    Example: 'nsamp',1000

    Data Types: double

    plots —Plot on the screen.scalar.

    If plots=1 the fan plot is produced else (default) no plot is produced.

    REMARK: all the following options work only if plots=1

    Example: 'plots',1

    Data Types: double

    conflev —Confidence level.scalar | vector.

    Confidence level for the bands (default is 0.99, that is we plot two horizontal lines in correspondence of value -2.58 and 2.58).

    Example: 'conflev',[0.9 0.95 0.99]

    Data Types: double

    FontSize —font size of the labels of the axes.scalar.

    Default value is 12.

    Example: 'FontSize',20

    Data Types: double

    labx —a label for the x-axis.character.

    default: 'Subset size m'

    Example: 'labx','my labx'

    Data Types: char

    laby —a label for the y-axis.character.

    default:'Score test statistic'

    Example: 'laby','my laby'

    Data Types: char

    lwd —linewidth of the curves which contain the score test.scalar.

    Default line width=2.

    Example: 'lwd',5

    Data Types: double

    lwdenv —width of the lines associated with the envelopes.scalar.

    Default is lwdenv=1.

    Example: 'lwdenv',5

    Data Types: double

    SizeAxesNum —Scalar which controls the size of the numbers of the axes.scalar.

    Default value is 10.

    Example: 'SizeAxesNum',12

    Data Types: double

    tag —handle of the plot which is about to be created.character.

    The default is to use tag 'pl_fan'. Notice that if the program finds a plot which has a tag equal to the one specified by the user, then the output of the new plot overwrites the existing one in the same window else a new window is created

    Example: 'tag','mytag'

    Data Types: char

    titl —a label for the title.character.

    default: 'Fan plot'

    Example: 'titl','my title'

    Data Types: char

    xlimx —Minimum and maximum of the x axis.vector.

    Default value is [init n]

    Example: 'xlimx',[0 1]

    Data Types: double

    ylimy —Minimum and maximum of the y axis.vector.

    Default value for ylimy(1)=max(min(score_test),-20).

    Default value for ylimy(2)=min(max(score_test),20).

    Example: 'ylimy',[0 1]

    Data Types: double

    Output Arguments

    expand all

    out — description Structure

    Structure which contains the following fields

    Value Description
    Score

    (n-init+1) x length(la)+1 matrix containing the values of the signed sqrt LR test for each value of the transformation parameter: 1st col = fwd search index;

    2nd col = value of the signed sqrt LR test in each step of the fwd search for la(1);

    ...........

    end col = value of the signed sqrt LR test test in each step of the fwd search for la(end).
    Exflag

    (n-init+1) x *length(la)+1 matrix containing the reason fminunc stopped in the maximization of the unconstrained likelihood. Matrix of integers.

    Column 2 is associated with the search which has ordered the data using la(1);

    .........

    Column *length(la)+1 is associated with the search which has ordered the data using la(length(la)).
    laMLE

    (n-init+1) x *length(la)+1 matrix containing the values of the maximum likelihood estimate of lambda.

    Column 2 is associated with the search which has ordered the data using la(1);

    .........

    Column *length(la)+1 is associated with the search which has ordered the data using la(length(la)).
    la

    vector containing the values of lambda for which fan plot is constructed
    bs

    matrix of size p x length(la) containing the units forming the initial subset for each value of lambda
    Un

    cell of size length(la).

    out.Un{i} is a n-init) x 11 matrix which contains the unit(s) included in the subset at each step in the search associated with la(i).

    REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one. Un(1,:), for example, contains the unit included in step init+1 ... ; Un(end,2) contains the units included in the final step of the search
    y

    A vector with n elements that contains the response variable which has been used
    X

    Data matrix of explanatory variables which has been used (it also contains the column of ones if input option intercept was missing or equal to 1)
    class

    'FSRfanTobit'.

    References

    See Also

    | | | | | | |

    This page has been automatically generated by our routine publishFS