FSRtsbsb
FSRtsbsb returns the units belonging to the subset in each step of the forward search
Description
Examples
FSRtsbsb with all default options.
load('fishery');
y=fishery{:,2};
bsbini=[97 77 12 2 26 95 10 60 94 135 7 61 114];
[Un,BB]=FSRtsbsb(y,bsbini);
 FSRtsbsb with optional arguments.
FSRtsbsb with optional arguments.
 FSRtsbsb with optional arguments.
FSRtsbsb with optional arguments.Load airline data 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960.
y = [112 115 145 171 196 204 242 284 315 340 360 417 % Jan
118 126 150 180 196 188 233 277 301 318 342 391 % Feb
132 141 178 193 236 235 267 317 356 362 406 419 % Mar
129 135 163 181 235 227 269 313 348 348 396 461 % Apr
121 125 172 183 229 234 270 318 355 363 420 472 % May
135 149 178 218 243 264 315 374 422 435 472 535 % Jun
148 170 199 230 264 302 364 413 465 491 548 622 % Jul
148 170 199 242 272 293 347 405 467 505 559 606 % Aug
136 158 184 209 237 259 312 355 404 404 463 508 % Sep
119 133 162 191 211 229 274 306 347 359 407 461 % Oct
104 114 146 172 180 203 237 271 305 310 362 390 % Nov
118 140 166 194 201 229 278 306 336 337 405 432 ]; % Dec
y=(y(:));
% Define the model and show the monitoring units plots.
model=struct;
model.trend=1; % linear trend
model.s=12; % monthly time series
model.seasonal=104; % four harmonics with time varying seasonality
bsbini=[97 77 12 2 26 95 10 60 94 135 7 61 114];
[Un,BB]=FSRtsbsb(y,bsbini,'model',model,'plots',1);
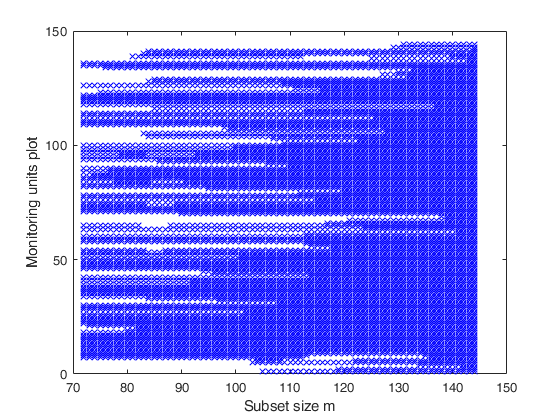
 Monitoring the units belonging to subset.
Monitoring the units belonging to subset.
 Monitoring the units belonging to subset.
Monitoring the units belonging to subset.Load airline data.
% 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960
y = [112 115 145 171 196 204 242 284 315 340 360 417 % Jan
118 126 150 180 196 188 233 277 301 318 342 391 % Feb
132 141 178 193 236 235 267 317 356 362 406 419 % Mar
129 135 163 181 235 227 269 313 348 348 396 461 % Apr
121 125 172 183 229 234 270 318 355 363 420 472 % May
135 149 178 218 243 264 315 374 422 435 472 535 % Jun
148 170 199 230 264 302 364 413 465 491 548 622 % Jul
148 170 199 242 272 293 347 405 467 505 559 606 % Aug
136 158 184 209 237 259 312 355 404 404 463 508 % Sep
119 133 162 191 211 229 274 306 347 359 407 461 % Oct
104 114 146 172 180 203 237 271 305 310 362 390 % Nov
118 140 166 194 201 229 278 306 336 337 405 432 ]; % Dec
y=(y(:));
% Contaminates units 31:40
y(31:40)=y(31:40)+200;
% Define the model and show the monitoring units plots.
model=struct;
model.trend=1; % linear trend
model.s=12; % monthly time series
model.seasonal=104; % four harmonics with time varying seasonality
bsbini=[97 77 12 2 26 95 10 60 94 135 7 61 114];
[Un,BB]=FSRtsbsb(y,0,'model',model,'plots',1);
% Create the 'monitoring units plot'
figure;
seqr=[Un(1,1)-1; Un(:,1)];
plot(seqr,BB','bx');
xlabel('Subset size m');
ylabel('Monitoring units plot');
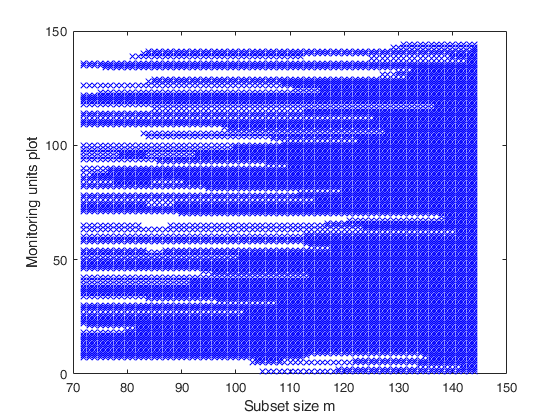
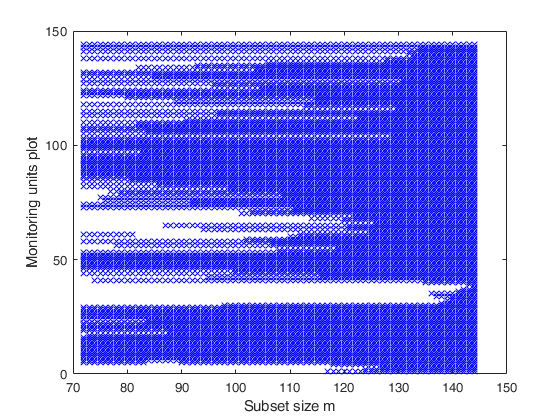
% The plot, which monitors the units belonging to subset in each step of
% the forward search, shows that independently of the initial starting
% point the contaminated units (31:40) are always the last to enter the
% forward search.
Input Arguments
y — Time series to analyze.
Vector.
A row or a column vector with T elements, which contains the time series.
Data Types: single| double
bsb — list of units forming the initial subset.
Vector | 0.
If bsb=0, then the procedure starts with p units randomly chosen, else if bsb is not 0, the search will start with m0=length(bsb).
Data Types: single| double
Name-Value Pair Arguments
Specify optional comma-separated pairs of Name,Value arguments.
Name is the argument name and Value
is the corresponding value. Name must appear
inside single quotes (' ').
You can specify several name and value pair arguments in any order as
Name1,Value1,...,NameN,ValueN.
'init',100 starts monitoring from step m=100
, 'model', model
, 'nocheck',false
, 'plots',1
, 'bsbmfullrank',1
init
—Start of monitoring point.scalar.
It specifies the point where to initialize the search and start monitoring required diagnostics. If it is not specified, it is set equal floor(0.5*(T+1)).
Example: 'init',100 starts monitoring from step m=100
Data Types: double
model
—model type.structure.
A structure which specifies the model which will be used. The model structure contains the following fields:
| Value | Description |
|---|---|
s |
scalar (length of seasonal period). For monthly data s=12 (default), for quarterly data s=4, ... |
trend |
scalar (order of the trend component). trend = 1 implies linear trend with intercept (default), trend = 2 implies quadratic trend and so on. Admissible values for trend are, 0, 1, 2 and 3. |
seasonal |
scalar (integer specifying number of frequencies, i.e. harmonics, in the seasonal component). Possible values for seasonal are , where [s/2]=floor(s/2). For example: if seasonal =1 (default) we have: \beta_1 \cos( 2 \pi t/s) + \beta_2 sin ( 2 \pi t/s); if seasonal =2 we have: \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s) + \beta_3 \cos(4 \pi t/s) + \beta_4 \sin (4 \pi t/s). Note that when s is even the sine term disappears for j=s/2 and so the maximum number of trigonometric parameters is s-1. If seasonal is a number greater than 100, then it is possible to specify how the seasonal component grows over time. For example, seasonal =101 implies a seasonal component which just uses one frequency which grows linearly over time as follows: (1+\beta_3 t)\times ( \beta_1 cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s)). For example, seasonal =201 implies a seasonal component which just uses one frequency which grows in a quadratic way over time as follows: (1+\beta_3 t + \beta_4 t^2)\times( \beta_1 \cos( 2 \pi t/s) + \beta_2 \sin ( 2 \pi t/s)). seasonal =0 implies a non seasonal model. |
X |
matrix of size T-by-nexpl containing the values of nexpl extra covariates which are likely to affect y. |
posLS |
positive integer which specifies the position to include the level shift component. For example, if model.posLS =13 then the explanatory variable I(t \geq 13}) is created. If this field is not present or if it is empty, the level shift component is not included. |
B |
column vector or matrix containing the initial values of parameter estimates which have to be used in the maximization procedure. If model.B is a matrix, then initial estimates are extracted from the first column of this matrix. If this field is empty or if this field is not present, the initial values to be used in the maximization procedure are referred to the OLS parameter estimates of the linear part of the model. The parameters associated to time varying amplitude are initially set to 0. Remark: the default model is for monthly data with a linear trend (2 parameters) + seasonal component with just one harmonic (2 parameters), no additional explanatory variables and no level shift that is: model=struct; model.s=12; model.trend=1; model.seasonal=1; model.X=''; model.posLS=''; |
Example: 'model', model
Data Types: struct
nocheck
—Check input arguments.boolean.
If nocheck is equal to true, no check is performed on supplied structure model.
Example: 'nocheck',false
Data Types: logical
bsbsteps
—Save the units forming subsets in selected steps.vector.
It specifies for which steps of the fwd search it is necessary to save the units forming subset. If bsbsteps is 0, we store the units forming subset in all steps. The default is to store the units forming subset in all steps if n<=5000, else to store the units forming subset at steps init and steps which are multiples of 100. For example, as default, if n=7530 and init=6, units forming subset are stored for m=init, 100, 200, ..., 7500.
Example: 'bsbsteps',[100 200] stores the unis forming
subset in steps 100 and 200.
Data Types: double
plots
—Plot on the screen.scalar.
If plots=1 the monitoring units plot is displayed on the screen. The default value of plots is 0 (that is no plot is produced on the screen).
Example: 'plots',1
Data Types: double
bsbmfullrank
—What to do in case subset at step m (say bsbm) produces a
non singular X.scalar.
This option controls what to do when rank(X(bsbm,:)) is smaller than the number of explanatory variables.
If bsbmfullrank = 1 (default is 1), these units (whose number is say mnofullrank) are constrained to enter the search in the final n-mnofullrank steps, else the search continues using as estimate of beta at step m, the estimate of beta found in the previous step.
Example: 'bsbmfullrank',1
Data Types: double
Output Arguments
Un —Units included in each step.
Matrix
(n-init) x 11 Matrix which contains the unit(s) included in the subset at each step of the search.
REMARK: in every step the new subset is compared with the old subset. Un contains the unit(s) present in the new subset but not in the old one.
Un(1,2), for example, contains the unit included in step init+1.
Un(end,2) contains the units included in the final step of the search.
BB —Units belonging to subset in each step or selected steps.
Matrix
n-by-(n-init+1) or n-by-length(bsbsteps) matrix which contains the units belonging to the subset at each step (or in selected steps as specified by optional vector bsbsteps) of the forward search.
More precisely: BB(:,1) contains the units forming subset in step bsbsteps(1);
....;
BB(:,end) contains the units forming subset in step bsbsteps(end);
Row 1 of matrix BB is referred to unit 1;
......;
Row n of matrix BB is referred to unit n;
Units not belonging to subset are denoted with NaN.
References
Atkinson, A.C. and Riani, M. (2006), Distribution theory and simulations for tests of outliers in regression, "Journal of Computational and Graphical Statistics", Vol. 15, pp. 460-476.
Riani, M. and Atkinson, A.C. (2007), Fast calibrations of the forward search for testing multiple outliers in regression, "Advances in Data Analysis and Classification", Vol. 1, pp. 123-141.
Rousseeuw, P.J., Perrotta D., Riani M. and Hubert, M. (2018), Robust Monitoring of Many Time Series with Application to Fraud Detection, "Econometrics and Statistics". [RPRH]

