overlapmap

overlapmap produces an interactive overlap map

expand all in page

Syntax

Description

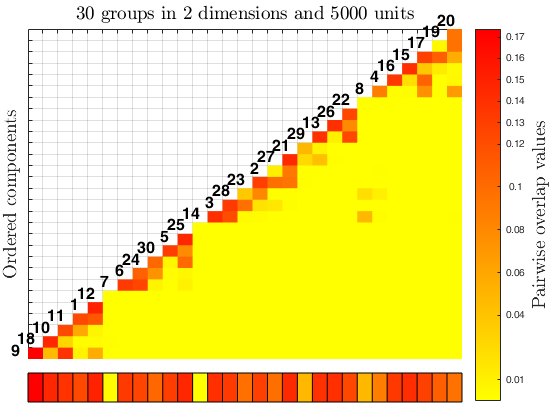
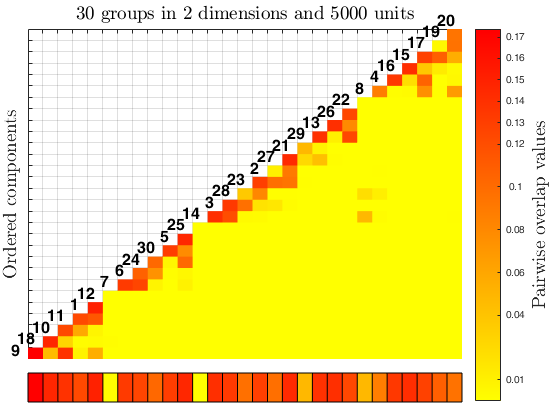
The function overlapmap plots the ordered pairwise overlap values between components. These components are ordered according to a specific rule: first the closest pair is plotted in the lowest left corner, then the components closer to the ones already included are plotted (when all of them have a zero overlap value with the ones already included, the closest pair between all the remaining ones is inserted). The overlap map can either shows with different colors the closeness between components (i.e. in a descriptive manner), or it becomes an interactive plot with a left click on the color bar, which find and visualize the closest components according to a specific threshold value $ \omega^* $ (i.e. omegaStar), which specifies the minimum paiwise overlap threshold value used to merge the components. The interactive process ends with a right click on the white grid in the upper left corner of the plot, it also updates the results creating in the workspace a new variable 'userOverlap'. See the More About section for further informations.

example

out =overlapmap(D) Example using tkmeans on geyser data.

example

out =overlapmap(D, Name, Value) Example using M5data with tclust and tkmeans, specifying an initial threshold omegaStar, a colormap, and allowing for additional interactive plots.

Examples

expand all

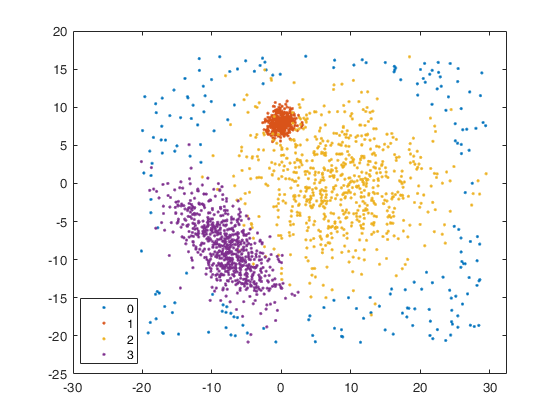
  • Example using tkmeans on geyser data.

    • close all
Y = load('geyser2.txt');
k = 3;
% using tkmeans
out = tkmeans(Y, k*2, 0.05, 'plots', 1);
overl_1 = overlapmap(out);
% using tkmeans for a higher number of components
out2 = tkmeans(Y, k*4, 0.05, 'plots', 1);
overl_2 = overlapmap(out2);
cascade;
    Total estimated time to complete trimmed k means:  0.04 seconds 
Warning: Colon operands must be real scalars. This warning will become an
error in a future release. 
Total estimated time to complete trimmed k means:  0.14 seconds 
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
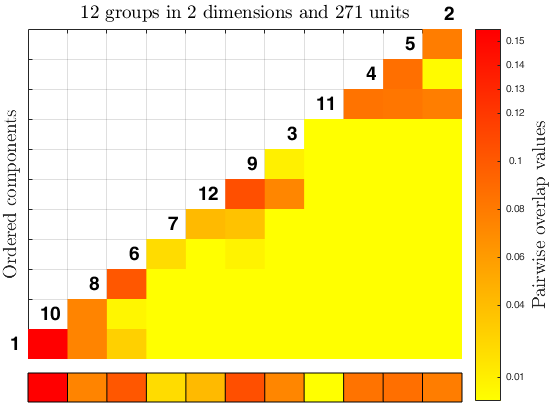
    Click here for the graphical output of this example (link to Ro.S.A. website).

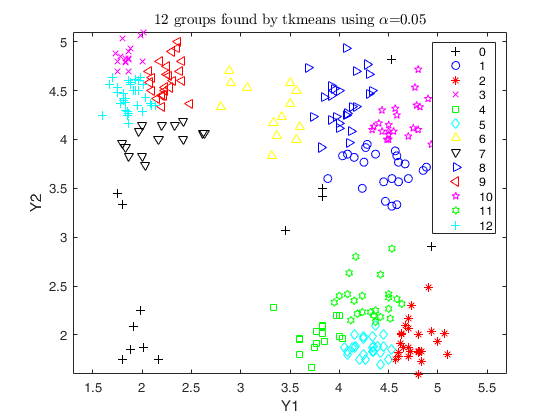
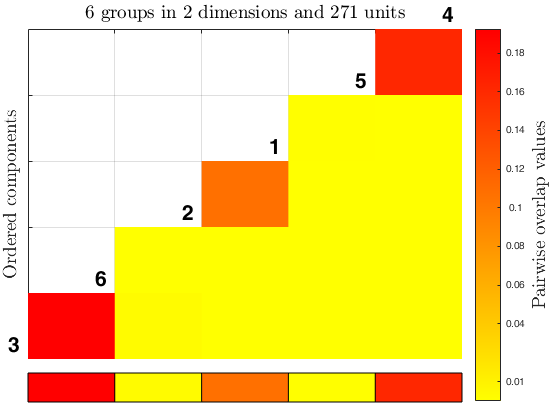
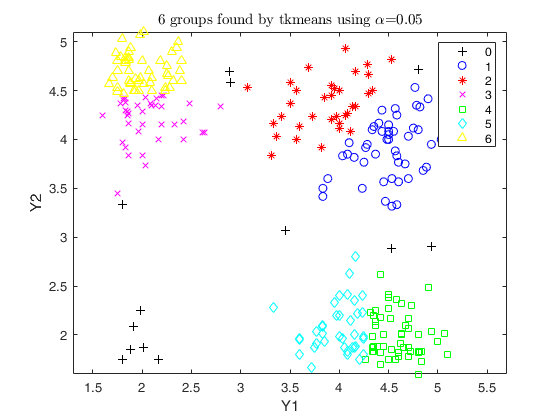
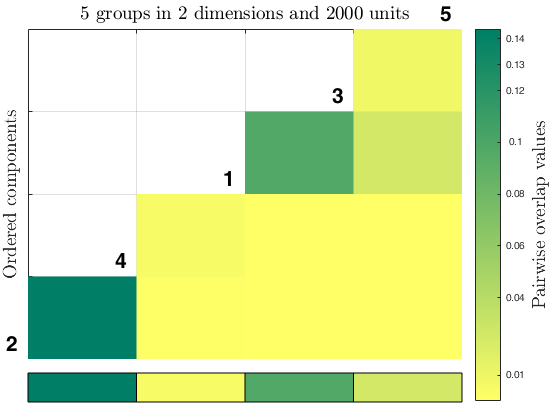
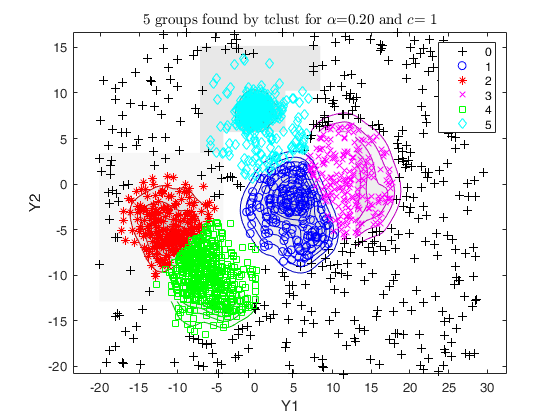
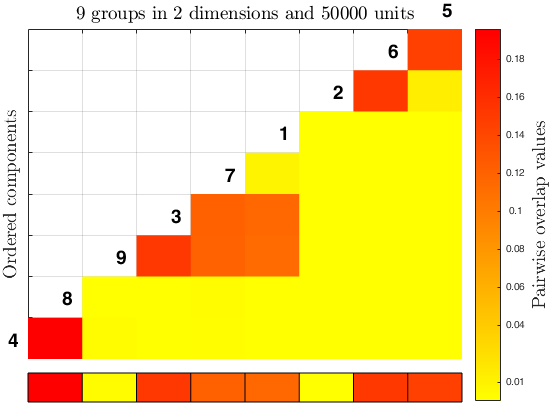
  • Example using M5data with tclust and tkmeans, specifying an initial threshold omegaStar, a colormap, and allowing for additional interactive plots.

    • close all
rng('default')
rng(2)
Y=load('M5data.txt');
gscatter(Y(:,1),Y(:,2), Y(:,3))
k = 3;
out = tkmeans(Y(:,1:2), k*5, 0.2, 'plots', 'ellipse', 'Ysave', true);
overl = overlapmap(out, 'omegaStar', 0.025, 'plots', 'contour', 'userColors', winter);
rng('default')
if verLessThan('matlab', '8.5')
rng(5)
else
rng(1)
end
out_2 = tclust(Y(:,1:2), k*2, 0.2, 1, 'plots', 'contourf', 'Ysave', true);
overl_2 = overlapmap(out_2, 'omegaStar', 0.0025, 'plots', 'contourf', 'userColors', summer);
cascade;
    Total estimated time to complete trimmed k means:  2.00 seconds 
------------------------------
Warning: Number of subsets without convergence equal to 36%
Warning: Colon operands must be real scalars. This warning will become an
error in a future release. 
ClaLik with untrimmed units selected using crisp criterion
Total estimated time to complete tclust:  2.50 seconds 
Number of supplied clusters =6
Number of estimated clusters =5
Warning: The total number of estimated clusters is smaller than the number
supplied 
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
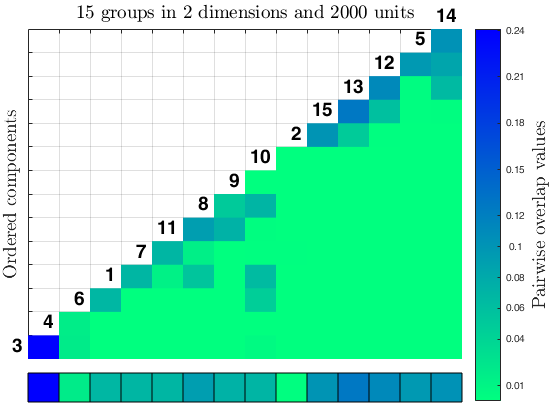
    Click here for the graphical output of this example (link to Ro.S.A. website).

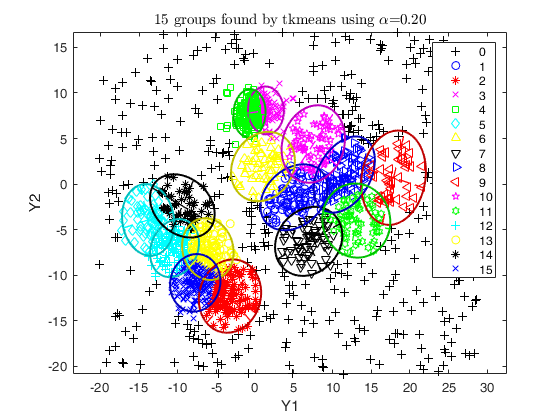
    Related Examples

    expand all

  • Example using simdataset to create homogeneous and spherical clusters.

    • This output is used as input for the overlap map and then also tkmeans and tclust solutions, for a higher number of components. 

    close all
% Specify k cluster in v dimensions with n obs
k = 8;
v = 4;
n = 5000;
% Generate 8 homogeneous spherical clusters
rng('default')
rng(10);
out = MixSim(k, v, 'sph', true, 'hom', true, 'int', [0 10], 'Display', ...
'off', 'MaxOmega', 0.005, 'Display','off');
% 5 percent noise
alpha0 = 0.05*n;
% Simulating data
[X, id] = simdataset(n, out.Pi, out.Mu, out.S, 'noiseunits', alpha0);
% Plotting data
figure;
spmplot(X, 'group', id);
str = sprintf('Simulated data with %d groups in %d dimensions and %d units', k, v, n);
title(str,'Interpreter','Latex');
% overlap map on simdataset output
Inputs.Y = X;
Inputs.idx = id;
overlapmap(Inputs, 'plots', 'contourf');
% overlap map on tkmeans solution for simdataset output
out = tkmeans(X, k*4, 0.05, 'plots', 'contourf', 'Ysave', true);
overlapmap(out, 'plots', 'contourf');
out = tclust(X, 10, 0.05, 100, 'plots', 'contour', 'Ysave', true);
overlapmap(out, 'plots', 'contourf');
cascade;

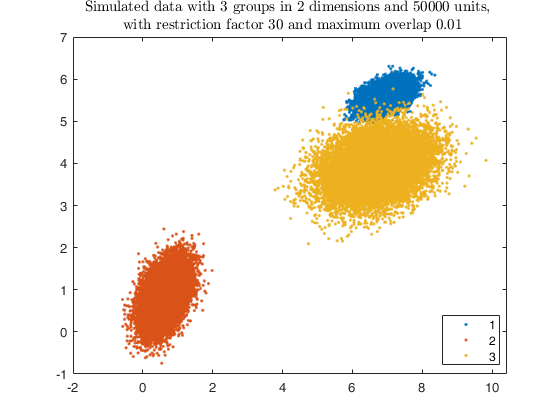
  • Example using simdataset to create heterogeneous and elliptical clusters and using tkmeans output as input for the overlap map.

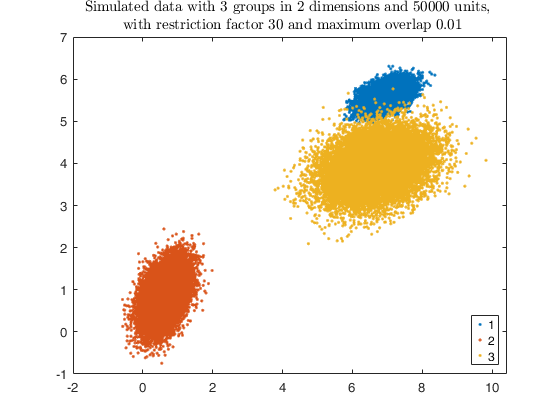
    • close all
% Specify k cluster in v dimensions with n obs
k = 3;
v = 2;
n = 50000;
% restriction factor
restr = 30;
% Maximum overlap
maxOm = 0.005;
% Generate heterogeneous and elliptical clusters
rng('default')
rng(500, 'twister');
out = MixSim(k, v, 'sph', false, 'restrfactor', restr, 'int', [0 10], ...
'Display', 'off', 'MaxOmega', maxOm, 'Display','off');
% null noise
alpha0 = 0;
% Simulating data
[X, id] = simdataset(n, out.Pi, out.Mu, out.S, 'noiseunits', alpha0);
% Plotting data
gg = gscatter(X(:,1), X(:,2), id);
str = sprintf('Simulated data with %d groups in %d dimensions and %d units, \n with restriction factor %d and maximum overlap %.2f', ...
k, v, n, restr, maxOm);
title(str,'Interpreter','Latex');
% use tkmeans for a larger number of cluster and without trimming
tkm = tkmeans(X, k*3, 0,'plots', 2,'Ysave',true, 'plots', 'ellipse');
% overlap map with interctive mode
overl = overlapmap(tkm, 'omegaStar', 0.01, 'plots', 'contourf');
cascade;
    Total estimated time to complete trimmed k means: 45.23 seconds 
------------------------------
Warning: Number of subsets without convergence equal to 37.3333%
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
    Click here for the graphical output of this example (link to Ro.S.A. website)

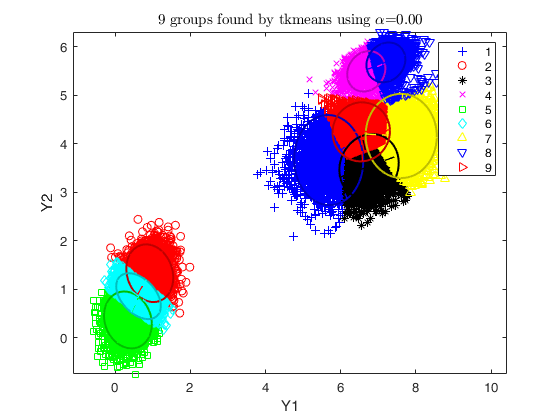
  • Example using simdataset to create homogeneous and spherical clusters and using tkmeans.

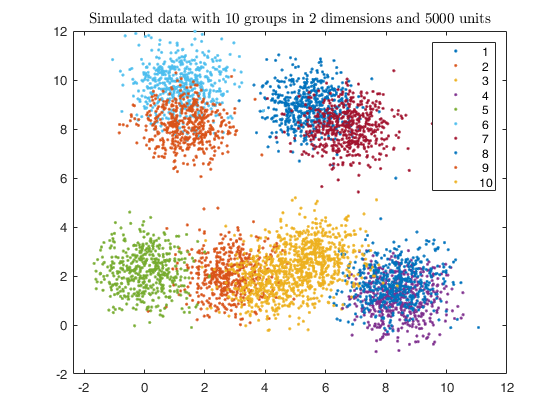
    • clear variables; close all
% Specify k cluster in v dimensions with n obs
k = 10;
v = 2;
n = 5000;
% Generate homogeneous and spherical clusters
rng('default')
rng(100, 'twister');
out = MixSim(k, v, 'sph', true, 'hom', true, 'int', [0 10], 'Display', 'off', 'BarOmega', 0.05, 'Display','off');
% Simulating data
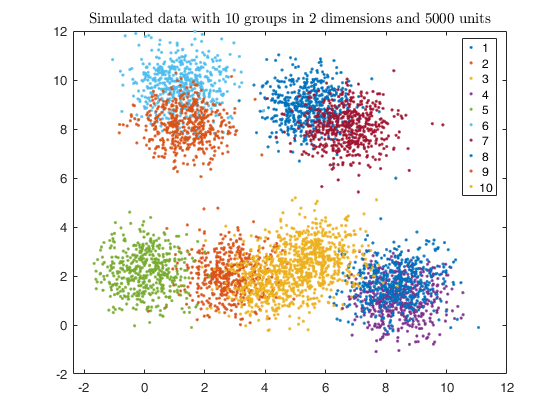
[X, id] = simdataset(n, out.Pi, out.Mu, out.S);
% Plotting data
gscatter(X(:,1), X(:,2), id);
str = sprintf('Simulated data with %d groups in %d dimensions and %d units', k, v, n);
title(str,'Interpreter','Latex');
clickableMultiLegend(num2str((1:k)'));
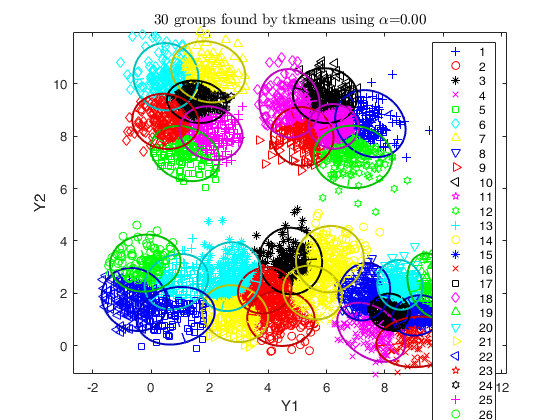
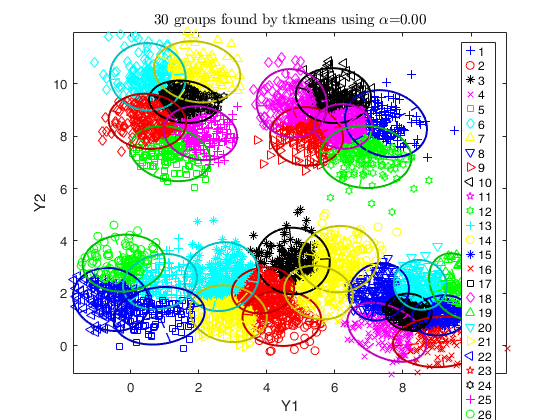
% use tkmeans for a larger number of cluster and without trimming
tkm = tkmeans(X, k*3, 0,'plots', 2,'Ysave',true, 'plots', 'ellipse');
% overlap map with interctive mode
out = overlapmap(tkm, 'omegaStar', 0.01, 'plots', 'contourf');
cascade;
    Total estimated time to complete trimmed k means: 10.09 seconds 
------------------------------
Warning: Number of subsets without convergence equal to 36%
Warning: Colon operands must be real scalars. This warning will become an
error in a future release.
    Click here for the graphical output of this example (link to Ro.S.A. website)

    Input Arguments

    expand all

    D — Informations to compute the overlap matrix. Structure.

    D is a structure which can have the following fields (not all of them are strictly required).

    Admissable fields for the structure D:

    Value Description
    idx

    Label of the units. Vector. It is a vector with n elements which assigns each unit to one of the k groups.

    REMARK - labels<=0 denotes trimmed units.
    Y

    Input data. Matrix. Data matrix containining n observations on v variables. Rows of Y represent observations, and columns represent variables. Missing values (NaN's) and infinite values (Inf's) are allowed, since observations (rows) with missing or infinite values will automatically be excluded from the computations.

    When this field is specified the algorithm evaluate the statistics of interest to obtain the overlap matrix, it also allows the user to obtain additional plots when the interaction is closed (using spmplot). When this field is not specified the fields D.sigmaopt, D.muopt and D.siz are required.
    sigmaopt

    v-by-v-by-k covariance matrices of the groups.
    muopt

    k-by-v matrix containing cluster centroid locations.
    siz

    Matrix or vector. If it is a matrix of size k-by-3, where: 1st col = labels of the k components.

    2nd col = number of observations in each component.

    3rd col = percentage of observations in each component.

    REMARK: in case there is a field structure named emp containing the same informations, these ones will be used

    Data Types: struct

    Name-Value Pair Arguments

    Specify optional comma-separated pairs of Name,Value arguments. Name is the argument name and Value is the corresponding value. Name must appear inside single quotes (' '). You can specify several name and value pair arguments in any order as Name1,Value1,...,NameN,ValueN.

    Example: 'omegaStar', 0.01 , 'plots', 1 , 'userColors', winter

    omegaStar —Pairwise overlap threshold.scalar.

    It is the value between pairs of components considered disjunct if their overlap is below omegaStar. If specified, these components would be highlighted in the overlap map with an 'X' mark.

    The default value is 0 (i.e. all components should be merged).

    Example: 'omegaStar', 0.01

    Data Types: single | double

    plots —Additional plot on the screen.scalar, char | struct.

    This arguments requires the presence of the field D.Y.

    - If plots=0 (default) no additional plot is produced.

    - If plots=1, at the end of the interaction with the overlap map (i.e. right click on the white grid), the components merged are shown using the spmplot function. In particular: * for v=1, an histogram of the univariate data.

    * for v=2, a bivariate scatterplot.

    * for v>2, a scatterplot matrix.

    When v>=2 plots offers the following additional features (for v=1 the behaviour is forced to be as for plots=1): - plots='contourf' adds in the background of the bivariate scatterplots a filled contour plot. The colormap of the filled contour is based on grey levels as default.

    This argument may also be inserted in a field named 'type' of a structure. In the latter case it is possible to specify the additional field 'cmap', which changes the default colors of the color map used. The field 'cmap' may be a three-column matrix of values in the range [0,1] where each row is an RGB triplet that defines one color.

    Check the colormap function for additional informations.

    - plots='contour' adds in the background of the bivariate scatterplots a contour plot. The colormap of the contour is based on grey levels as default. This argument may also be inserted in a field named 'type' of a structure.

    In the latter case it is possible to specify the additional field 'cmap', which changes the default colors of the color map used. The field 'cmap' may be a three-column matrix of values in the range [0,1] where each row is an RGB triplet that defines one color.

    Check the colormap function for additional informations.

    - plots='ellipse' superimposes confidence ellipses to each group in the bivariate scatterplots. The size of the ellipse is chi2inv(0.95,2), i.e. the confidence level used by default is 95%. This argument may also be inserted in a field named 'type' of a structure. In the latter case it is possible to specify the additional field 'conflev', which specifies the confidence level to use and it is a value between 0 and 1.

    - plots='boxplotb' superimposes on the bivariate scatterplots the bivariate boxplots for each group, using the boxplotb function. This argument may also be inserted in a field named 'type' of a structure.

    If plots is a struct it may contain the following fields:

    Value Description
    type

    a char specifying the type of superimposition Choices are 'contourf', 'contour', 'ellipse' or 'boxplotb'.

    REMARK - The labels<=0 are automatically excluded from the overlaying phase, considering them as outliers.

    Example: 'plots', 1

    Data Types: single | double | string

    userColors —Color used for the color map.matrix | string.

    Check the colormap function for more informations.

    Example: 'userColors', winter

    Data Types: single | double | string

    Output Arguments

    expand all

    out — description Structure

    A structure containing the following fields

    Value Description
    Ghat

    Estimated number of clusters in the data.
    PairOver

    Pairwise overlap triangular matrix (sum of misclassification probabilities) among components found by tkmeans.
    mergID

    Label for each unit. It is a vector with n elements which assigns each unit to one of the groups obtained.

    REMARK - out.mergID<=0 denotes trimmed units.
    merged

    Cell array containing the labels of the components merged together.
    single

    Vector containing the labels of single clusters found, i.e. not merged with any other component.

    Optional Output: userOverlap : Updating of the results. Structure. userOverlap is obtained when the interaction with the overlap map is closed and is added in the Workspace.

    It contains the following fields, which represent an update of their corresponding variable in the structure out: - userOverlap.omegaStar = update of out.omegaStar.

    - userOverlap.Ghat = update of out.Ghat.

    - userOverlap.merged = update of out.merged.

    - userOverlap.single = update of out.single.

    More About

    expand all

    Additional Details

    In the code 'overM' represents a triangular matrix, denoted as $ \Omega $, which contains the pairwise overlap values. The merging phase starts searching the maximum pairwise overlap value in $ \Omega $, i.e. $ \max (\Omega_{k k'}) $, and then deletes this value (e.g. setting it to NaN).

    This new matrix obtained is denoted as $ \Omega' $. The respective rows and columns corresponding to the element deleted in $ \Omega' $ are placed in a new matrix $ \Omega'' $. The algorithm progressively continue the same process, searching the highest pairwise overlap value in the components closest to the ones previously found, i.e. in the respective rows or columns of the components $ k $ and $ k' $. When the latter are all zeros, the process starts again considering the remaining values in $ \Omega $.

    The values $ \max(\Omega'_{k k'}) $ and the respective $ k $ and $ k' $ labels are sequentially saved in a $ k(k-1)/2 \times 3 $ matrix MergMat.

    References

    Melnykov, V., Michael, S. (2020), Clustering Large Datasets by Merging K-Means Solutions, Journal of Classification, Vol. 37, pp. 97–123, https://doi.org/10.1007/s00357-019-09314-8

    Melnykov, V. (2016), Merging Mixture Components for Clustering Through Pairwise Overlap, "Journal of Computational and Graphical Statistics", Vol. 25, pp. 66-90.

    Acknowledgements

    ...

    See Also

    | |

    This page has been automatically generated by our routine publishFS