We assume that vectors x1 and x2 contain discrete observations from a bivariate diffusion
process $(x_1,x_2)$ following the Ito stochastic differential equation
$$dx^i(t)= \sigma^i(t) \ dW^i(t) + b^i(t) \ dt, \quad i=1,2,$$
where $W^1$ and $W^2$ are two Brownian motions defined on the filtered probability space
$(\Omega, (\mathcal{F}_t)_{t \in [0,T]}, P)$, with correlation $\rho$, while
$\sigma^1, \sigma^2, b^1$ and $b^2$ are random processes, adapted to $\mathcal{F}_t$.
See the References for further mathematical details.
The spot covariance $c$ between the processes $x^1$ and $x^2$ at time $t
\in [0,T]$ is defined as
$$c(t):= \frac{d \langle x^1, x^2 \rangle_t}{dt} = \rho \sigma^1(t) \sigma^2(t).$$
Let $i=1,2$. For any positive integer $n_i$, let $\mathcal{S}^i_{n_i}:=\{ 0=t^i_{0}\leq \cdots
\leq t^i_{n_i}=T \}$ be the observation times for the $i$-th asset. Moreover, let $\delta_l(x^i):=
x^i(t^i_{l+1})-x^i(t^i_l)$ be the increments of $x^i$.
The Fourier estimator of the spot covariance at time $t \in [0,T]$ is
given by
$$\widehat c_{n_1,n_2,N,M}(\tau)= \sum_{|k|\leq M} \left(1-{|k|\over
M}\right)c_k(c_{n_1,n_2,N}) \, e^{{\rm i}\frac{2\pi}{T}k\tau},$$
where:
$$c_k(c_{n_1,n_2,N})={T\over {2N+1}} \sum_{|s|\leq N} c_{s}(dx^1_{n_1})c_{k-s}(dx^2_{n_2}),$$
$$c_k(dx^i_{n_i})= {1\over {T}} \sum_{l=0}^{n_i-1} e^{-{\rm i}\frac{2\pi}{T}kt^i_l}\delta_{l}(x_i).$$
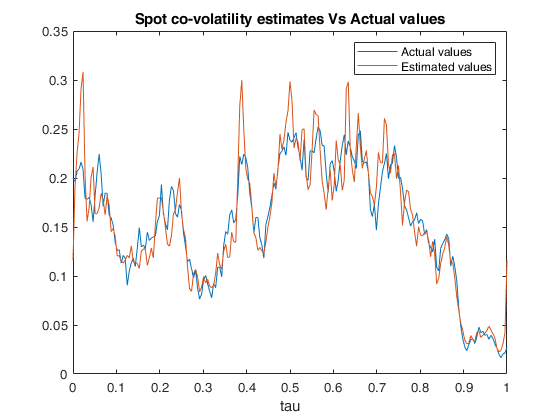
 Example of call of FM_spot_cov with default values of N, M and tau.
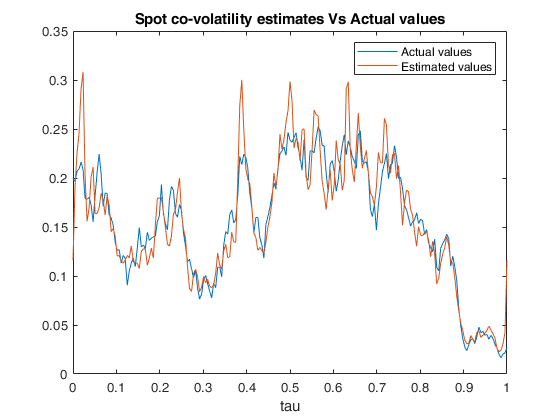
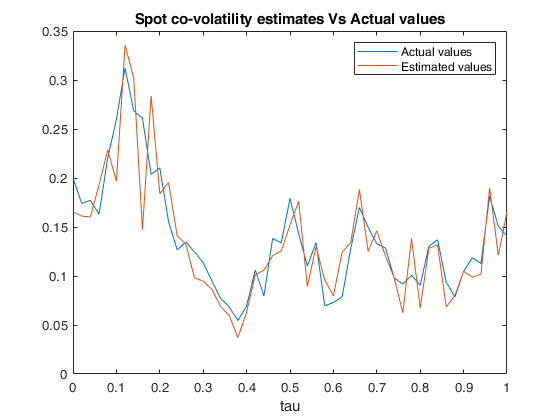
Example of call of FM_spot_cov with default values of N, M and tau.