FSRB
FSRB gives an automatic outlier detection procedure in Bayesian linear regression
Description
Examples
FSRB with optional arguments.
FSRB with optional arguments.
load hprice.txt; n=size(hprice,1); y=hprice(:,1); X=hprice(:,2:5); % set \beta components beta0=0*ones(5,1); beta0(2,1)=10; beta0(3,1)=5000; beta0(4,1)=10000; beta0(5,1)=10000; % \tau s02=1/4.0e-8; tau0=1/s02; % R prior settings R=2.4*eye(5); R(2,2)=6e-7; R(3,3)=.15; R(4,4)=.6; R(5,5)=.6; R=inv(R); % define a Bayes structure with previous data n0=5; bayes=struct; bayes.R=R; bayes.n0=n0; bayes.beta0=beta0; bayes.tau0=tau0; intercept=true; % function call out=FSRB(y,X,'bayes',bayes,'msg',0,'plots',1,'init',round(n/2),'intercept', intercept)
out =
struct with fields:
ListOut: [55 93 95 103 104 129 130 162 210 330 331 338 … ] (1×18 double)
outliers: [55 93 95 103 104 129 130 162 210 330 331 338 … ] (1×18 double)
mdr: [273×2 double]
Un: [273×11 double]
nout: [2×5 double]
beta: [5×1 double]
scale: 1.4951e+04
class: 'FSRB'
Related Examples
Example on Fishery dataset (analysis with intercept).
Example on Fishery dataset (analysis with intercept).nsamp is the number of subsamples to use in the frequentist analysis of first year, in order to find initial subset using LMS.
close all
nsamp=3000;
% threshold to be used to increase susbet of good units
threshold=300;
bonflev=0.99; % Bonferroni confidence level to be used for first year
bonflevB=0.99; % Bonferroni confidence level to be used for subsequent years
% Load 2002 Fishery dataset
Fishery2002=load('Fishery2002.txt');
y02=Fishery2002(:,3);
X02=Fishery2002(:,2);
n02=length(y02);
seq02=1:n02;
% frequentist Forward Search, 1st year
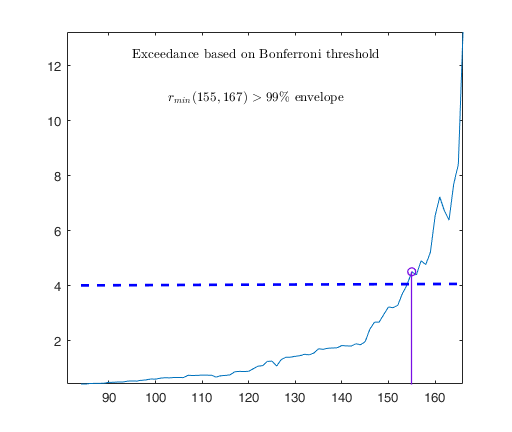
[out02]=FSR(y02,X02,'nsamp',nsamp,'plots',1,'msg',0,'init',round(n02*3/4),'bonflev',bonflev);
% In what follows
% g stands for good units
% i stand for intermediate units (i.e. units whose raw residual is smaller
% than threshold)
% o stands for outliers
% gi stands for good +intermediate units
% u02g = good units
% n02g = number of good units
u02g=setdiff(seq02,out02.ListOut);
n02g=length(u02g);
X02g=[ones(length(u02g),1) X02(u02g,:)];
y02g=y02(u02g);
% b02g = regression coefficients just using g units
b02g=X02g\y02g;
% res02 = squared raw residuals for all units using b02g
res02=(y02-[ones(length(X02),1) X02]*b02g).^2;
res02o=res02(out02.ListOut);
% sel= boolean vector which is true for the intermediate units
% (units whose squared residual is below the threshold)
sel=res02o<threshold^2;
% u02i = vector containing intermediate units (that is outliers whose
% residual is smaller than threshold)
u02i=out02.ListOut(sel);
% u02o = vector containing outliers whose residual is out of the threshold
u02o=out02.ListOut(~sel);
% u02gi = g + i units
if ~isempty(u02i)
u02gi=[u02g u02i];
else
u02gi=u02g;
end
% n02gi = number of good + intermediate units
n02gi=length(u02gi);
% plotting section
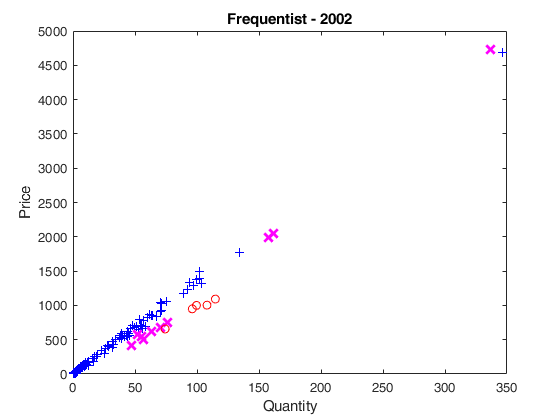
hold('off')
% good units, plotted as (+)
plot(X02(u02g)',y02(u02g)','Marker','+','LineStyle','none','Color','b')
hold('on')
% intermediate units plotted as (X)
plot(X02(u02i)',y02(u02i)','Marker','X','MarkerSize',9,'LineWidth',2,'LineStyle','none','Color','m')
% outliers, plotted as (O)
plot(X02(u02o)',y02(u02o)','Marker','o','LineStyle','none','Color','r')
xlabel('Quantity');
ylabel('Price');
title('Frequentist - 2002');
% S202gi = estimated of sigma^2 using g+i units
S202gi=sum(res02(u02gi))/(n02gi-2);
% X02gi = X matrix referred to good + intermediate units
X02gi=[ones(n02gi,1) X02(u02gi,:)];
% y02gi = y vector referred to good + intermediate units
y02gi=y02(u02gi);
% bayes = structure which contains prior information to be used in year
% 2003
bayes=struct;
bayes.beta0=b02g; % beta prior is beta based on g units
tau0=1/S202gi; % tau0 is based on g + i units
bayes.tau0=tau0;
R=X02g'*X02g; % R is based on g units
bayes.n0=n02gi; % n0 is based on g + i units
bayes.R=R;
% 2003
% Load 2003 Fishery dataset
Fishery2003=load('Fishery2003.txt');
y03=Fishery2003(:,3);
X03=Fishery2003(:,2);
n03=length(y03);
seq03=1:n03;
% Bayesian Forward Search, 2nd year
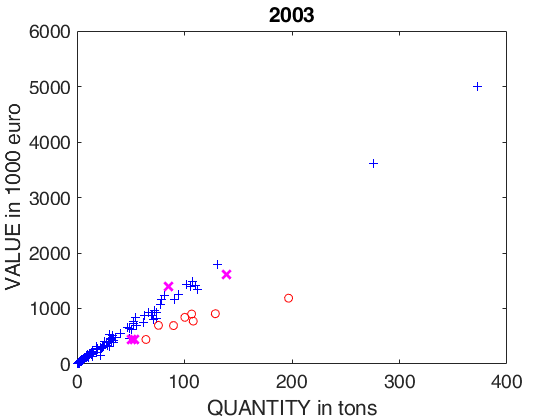
out03=FSRB(y03,X03,'bayes',bayes,'msg',0,'plots',1,'init',round(n03/2),'bonflev',bonflevB);
u03g=setdiff(seq03,out03.ListOut);
n03g=length(u03g);
% compute beta coefficient for year 2003 just using good units
X03g=[ones(n03g,1) X03(u03g,:)];
y03g=y03(u03g);
b03g=X03g\y03g;
res03=(y03-[ones(length(X03),1) X03]*b03g).^2;
res03o=res03(out03.ListOut);
sel=res03o<threshold^2;
% u03i = units to add to the good units subset (intermediate units)
u03i=out03.ListOut(sel);
% u03o = outliers out of the threshold
u03o=out03.ListOut(~sel);
if ~isempty(u03i)
u03gi=[u03g u03i];
else
u03gi=u03g;
end
n03gi=length(u03gi);
X03gi=[ones(n03gi,1) X03(u03gi,:)];
y03gi=y03(u03gi,:);
% plotting section
hold('off')
% good units, plotted as (+)
plot(X03(u03g)',y03(u03g)','Marker','+','LineStyle','none','Color','b')
hold('on')
% units below the threshold, plotted as (X)
plot(X03(u03i)',y03(u03i)','Marker','X','MarkerSize',9,'LineWidth',2,'LineStyle','none','Color','m')
% outliers, plotted as (O)
plot(X03(u03o)',y03(u03o)','Marker','o','LineStyle','none','Color','r')
set(gca,'FontSize',14)
xlabel('QUANTITY in tons')
ylabel('VALUE in 1000 euro')
title('2003');
% Definition of bayes structure (based on 2002 and 2003)
bayes=struct;
X02gX03g=[X02g; X03g];
y02gy03g=[y02g; y03g];
n02gn03g=n02g+n03g;
% b0203g prior estimate of beta for year 2004 is computed using good units
% for years 2002 and 2003
b0203g=X02gX03g\y02gy03g;
bayes.beta0=b0203g;
% R is just referred to good units for years 2002 and 2003
R=X02gX03g'*X02gX03g;
bayes.R=R;
% n0 is referred to g + i units in 2002 and 2003
bayes.n0=n02gi+n03gi;
X02giX03gi=[X02gi; X03gi];
y02giy03gi=[y02gi; y03gi];
% n02gin03gi = number of g+i units in 2002 and 2003
n02gin03gi=n02gi+n03gi;
% res = residuals for g+i units using b0203g
res=y02giy03gi-X02giX03gi*b0203g;
S203gi=sum(res.^2)/(n02gin03gi-2);
% estimate of tau is based on g + i units
tau0=1/S203gi;
bayes.tau0=tau0;
% Load 2004 Fishery dataset
Fishery2004=load('Fishery2004.txt');
y04=Fishery2004(:,3);
X04=Fishery2004(:,2);
n04=length(y04);
seq04=1:n04;
% Bayesian Forward Search, 3rd year
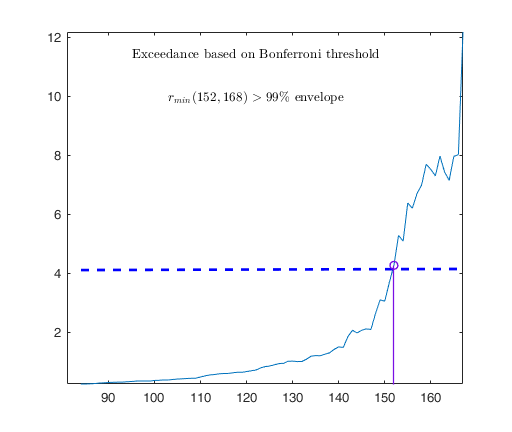
out04=FSRB(y04,X04,'bayes',bayes,'msg',0,'plots',1,'init',round(n04/2),'bonflev',bonflevB);
u04g=setdiff(seq04,out04.ListOut);
n04g=length(u04g);
X04g=[ones(n04g,1) X04(u04g,:)];
y04g=y04(u04g);
% b04g = beta based on good units for year 2004
b04g=X04g\y04g;
res04=(y04-[ones(length(X04),1) X04]*b04g).^2;
% res04o squared residuals for the tentative outliers
res04o=res04(out04.ListOut);
% we keep statistical units below the threshold
sel=res04o<threshold^2;
% u04i = units to add to the good units subset (intermediate units)
u04i=out04.ListOut(sel);
% u04o = units outliers out of the threshold
u04o=out04.ListOut(~sel);
if ~isempty(u04i)
u04gi=[u04g u04i];
else
u04gi=u04g;
end
n04gi=length(u04gi);
% plotting section
hold('off')
% good units, plotted as (+)
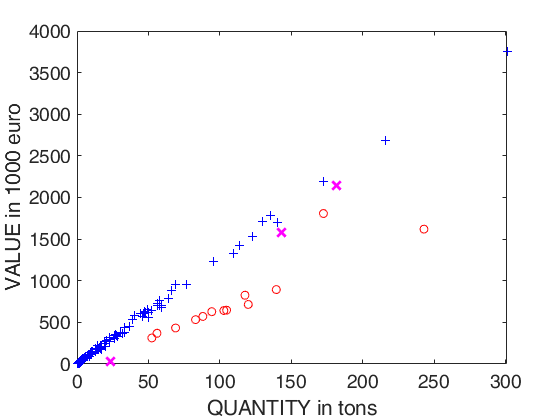
plot(X04(u04g)',y04(u04g)','Marker','+','LineStyle','none','Color','b')
hold('on')
% units below the treshold, plotted as (X)
plot(X04(u04i)',y04(u04i)','Marker','X','MarkerSize',9,'LineWidth',2,'LineStyle','none','Color','m')
% outliers, plotted as (O)
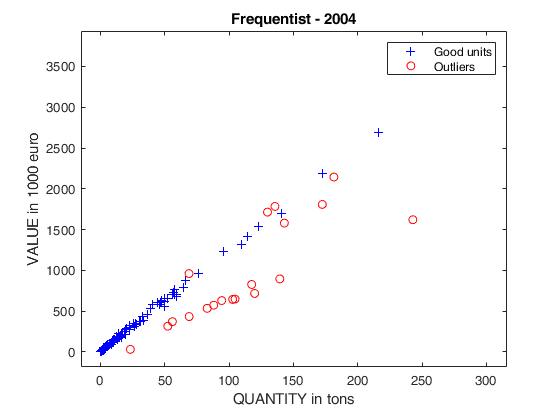
plot(X04(u04o)',y04(u04o)','Marker','o','LineStyle','none','Color','r')
set(gca,'FontSize',14)
xlabel('QUANTITY in tons')
ylabel('VALUE in 1000 euro')
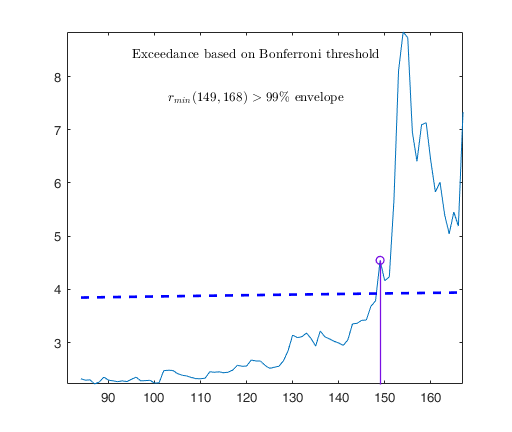
% frequentist Forward Search, 3rd year
out04=FSR(y04,X04,'nsamp',nsamp,'plots',1,'msg',0,'init',round(n04/2),'bonflev',bonflev);
xlabel('QUANTITY in tons')
ylabel('VALUE in 1000 euro')
title('Frequentist - 2004');
Example on Fishery dataset (analysis without the intercept).
Example on Fishery dataset (analysis without the intercept).
close all
% nsamp is the number of subsamples to use in the frequentist analysis of first
% year, in order to find initial subset using LMS.
nsamp=3000;
% threshold to be used to increase susbet of good units
threshold=300;
bonflev=0.99; % Bonferroni confidence level
% Load 2002 Fishery dataset
Fishery2002=load('Fishery2002.txt');
y02=Fishery2002(:,3);
X02=Fishery2002(:,2);
n02=length(y02);
seq02=1:n02;
% frequentist Forward Search, 1st year (regression without intercept)
[out02]=FSR(y02,X02,'intercept',false,'nsamp',nsamp,'plots',1,'msg',0,'init',round(n02*3/4),'bonflev',bonflev);
% In what follows
% g stands for good units
% i stand for intermediate units (i.e. units whose raw residual is smaller
% than threshold)
% o stands for outliers
% gi stands for good +intermediate units
% u02g = good units
% n02g = number of good units
u02g=setdiff(seq02,out02.ListOut);
X02g=X02(u02g,:);
y02g=y02(u02g);
% b02g = regression coefficients just using g units
% Note that b02g is a scalar because the intercept has not been added
b02g=X02g\y02g;
% res02 = squared raw residuals for all units using b02g
res02=(y02-X02*b02g).^2;
res02o=res02(out02.ListOut);
% sel= boolean vector which is true for the intermediate units
% (units whose squared residual is below the threshold)
sel=res02o<threshold^2;
% u02i = vector containing intermediate units (that is outliers whose
% residual is smaller than threshold)
u02i=out02.ListOut(sel);
% u02gi = g + i units
if ~isempty(u02i)
u02gi=[u02g u02i];
else
u02gi=u02g;
end
% n02gi = number of good + intermediate units
n02gi=length(u02gi);
% S202gi = estimated of sigma^2 using g+i units
S202gi=sum(res02(u02gi))/(n02gi-1);
% bayes = structure which contains prior information to be used in year
% 2003
bayes=struct;
bayes.beta0=b02g; % beta prior is beta based on g units
tau0=1/S202gi; % tau0 is based on g + i units
bayes.tau0=tau0;
R=X02g'*X02g; % R is based on g units
bayes.n0=n02gi; % n0 is based on g + i units
bayes.R=R;
% 2003
% Load 2003 Fishery dataset
Fishery2003=load('Fishery2003.txt');
y03=Fishery2003(:,3);
X03=Fishery2003(:,2);
n03=length(y03);
% Run Bayesian Forward Search for the 2nd year using the prior based on
% the first year.
out03=FSRB(y03,X03,'bayes',bayes,'msg',0,'plots',1,'init',round(n03/2),'bonflev',bonflev,'intercept',false);
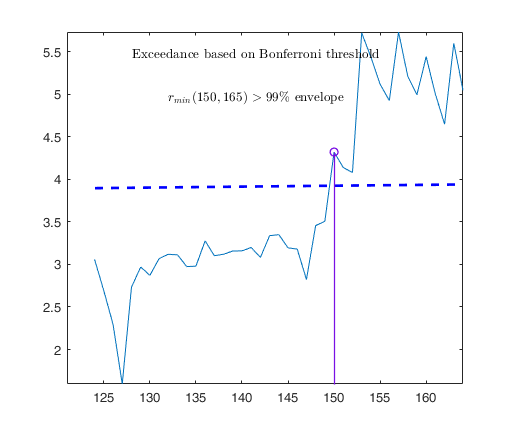
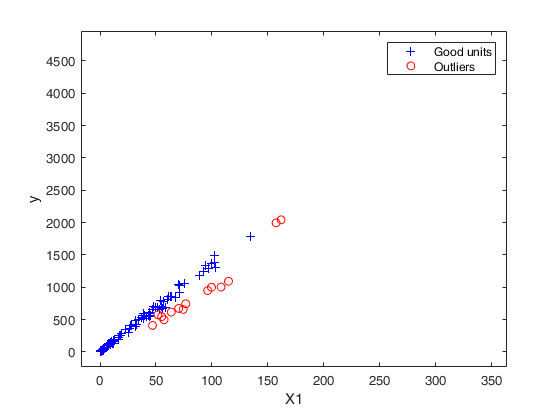
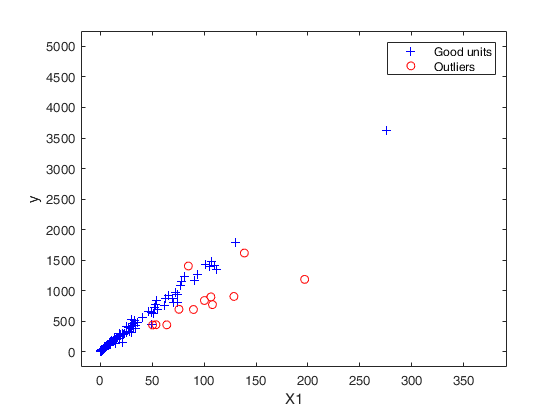
Outlier detection for Bank-Profit data.
Outlier detection for Bank-Profit data.
XX=load('BankProfit.txt');
R=load('BankProfitR.txt');
X=XX(:,1:end-1);
y=XX(:,end);
% Load prior information
beta0=zeros(10,1);
beta0(1,1)=-0.5;
beta0(2,1)=9.1; % Number of products (NUMPRO)
beta0(3,1)=0.001; % direct revenues (DIRREV)
beta0(4,1)=0.0002; % indirect revenues (INDREV)
beta0(5,1)=0.002; % savings accounts SAVACC
beta0(6,1)=0.12; % number of operations NUMOPE
beta0(7,1)=0.0004; % total amount of operations TOTOPE
beta0(8,1)=-0.0004; % Bancomat POS
beta0(9,1)=1.3; % Number of cards NUMCAR
beta0(10,1)=0.00004; % Amount in cards TOTCAR
% \tau
s02=10000;
tau0=1/s02;
% number of obs in which prior was based
n0=1500;
bayes=struct;
bayes.R=R;
bayes.n0=n0;
bayes.beta0=beta0;
bayes.tau0=tau0;
intercept=true;
n=length(y);
out=FSRB(y,X,'bayes',bayes,'msg',1,'plots',1,...
'init',round(n/2),'xlim',[1700 1905],'ylim',[2 4]);
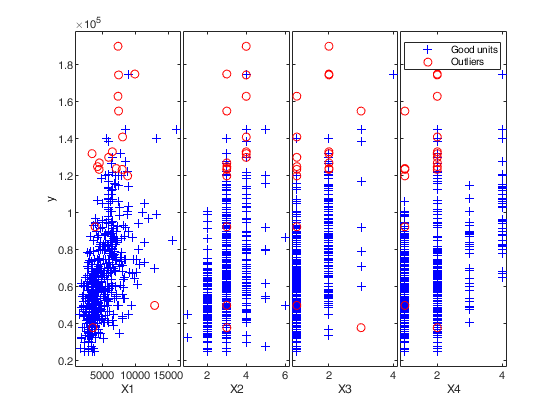
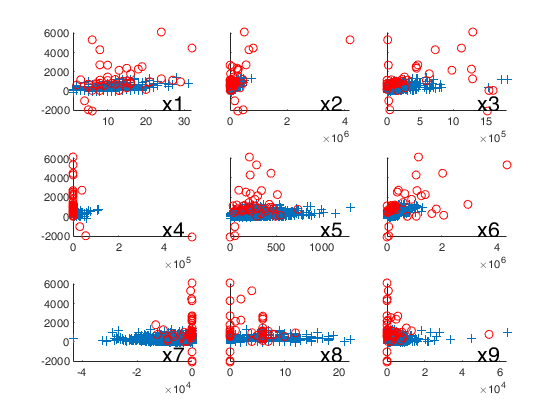
% Plot the outliers with a different symbol using a 3x3 layout.
selout=out.ListOut;
selin=setdiff(1:n,selout);
close all
% just in case user has additional function subtightplot
% http://www.mathworks.com/matlabcentral/fileexchange/39664-subtightplot
make_it_tight = false;
if make_it_tight == true && exist('subtightplot','file') ==2
subplot = @(m,n,p) subtightplot (m, n, p, [0.05 0.025], [0.1 0.01], [0.1 0.01]);
else
clear subplot;
end
% sel = panels in which yticks do not have to be removed
sel=[1 4 7];
miny=min(y);
maxy=max(y);
for j=1:9
subplot(3,3,j)
hold('on')
plot(X(selin,j),y(selin),'+')
plot(X(selout,j),y(selout),'ro')
ylim([miny maxy])
xlim([min(X(:,j)) max(X(:,j))])
if isempty(intersect(j,sel))
set(gca,'YTickLabel','')
end
% Add on the plot the variable name
text(0.75,0.1,['x' num2str(j)],'Units','normalized','FontSize',16)
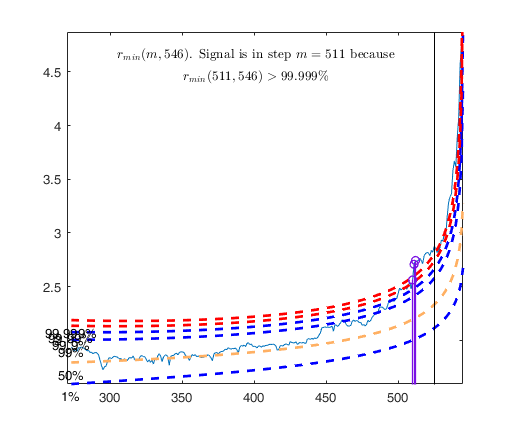
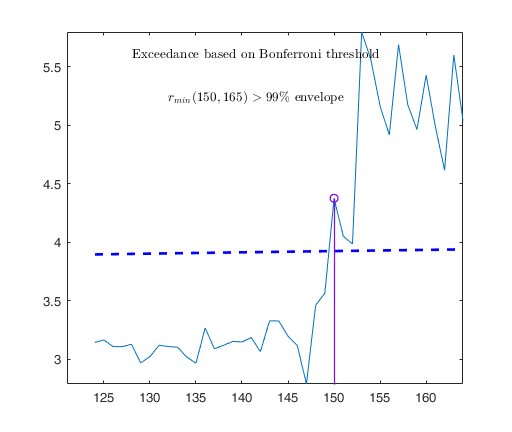
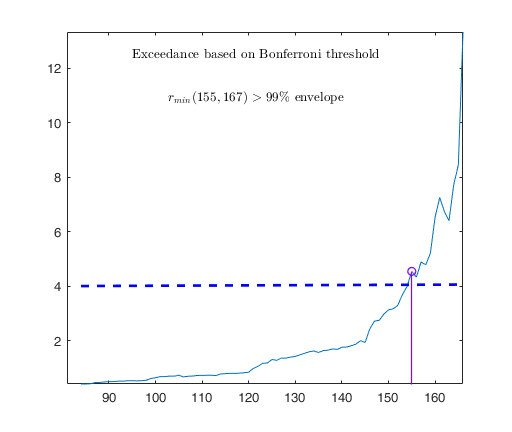
endObserved curve of r_min is at least 10 times greater than 99.99% envelope
--------------------------------------------------
-------------------------
Signal detection loop
Tentative signal in central part of the search: step m=1830 because
rmin(1830,1903)>99.999%
-------------------
Signal validation exceedance of upper envelopes
Validated signal
-------------------------------
Start resuperimposing envelopes from step m=1829
Superimposition stopped because r_{min}(1851,1859)>99.9% envelope
Subsample of 1858 units is homogeneous
----------------------------
Final output
Number of units declared as outliers=45
Summary of the exceedances
1 99 999 9999 99999
838 77 76 73 73
Input Arguments
Output Arguments
References
Chaloner, K. and Brant, R. (1988), A Bayesian Approach to Outlier Detection and Residual Analysis, "Biometrika", Vol. 75, pp. 651-659.
Riani, M., Corbellini, A. and Atkinson, A.C. (2018), Very Robust Bayesian Regression for Fraud Detection, "International Statistical Review", http://dx.doi.org/10.1111/insr.12247
Atkinson, A.C., Corbellini, A. and Riani, M., (2017), Robust Bayesian Regression with the Forward Search: Theory and Data Analysis, "Test", Vol. 26, pp. 869-886, https://doi.org/10.1007/s11749-017-0542-6